オプションを勉強するよ その3 オプションを組み合わせた戦略

満期(まで)に特定の行使価格で買う権利/売る権利(オプション)を組み合わせることで株価の値上がり値下がりに期待する以外の戦略を取れる。

オプション取引には行使価格が高い/低い、満期までの時間が近い/遠い、Callを買う/売る、Putを買う/売る、現物の株を買う/売るといった選択肢が存在する。

数々の戦略(スプレッド)はこれら選択肢の組み合わせである。

大きく動くか動かないかに賭ける、ストラドル

・行使価格が同じ
・満期までの時間が同じ
・CallとPutを1つずつ買う(ロングストラドル)または売る(ショートストラドル)

損益グラフはこのようになる

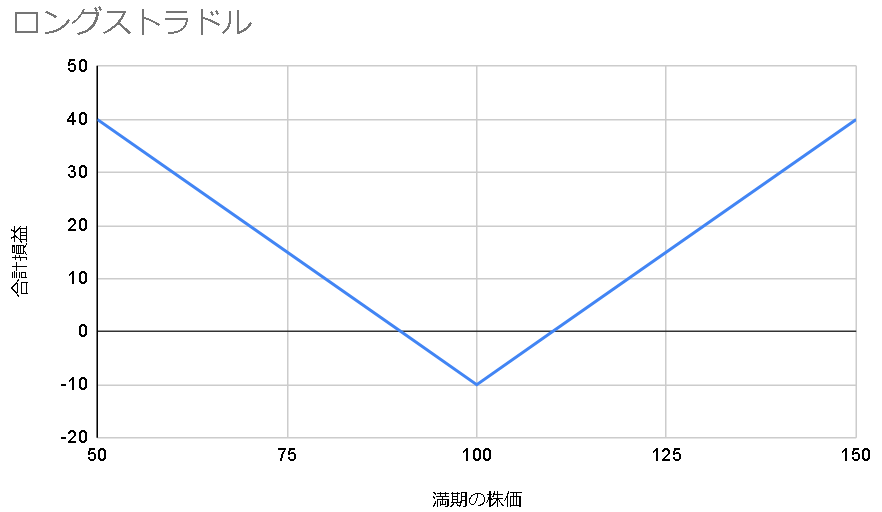
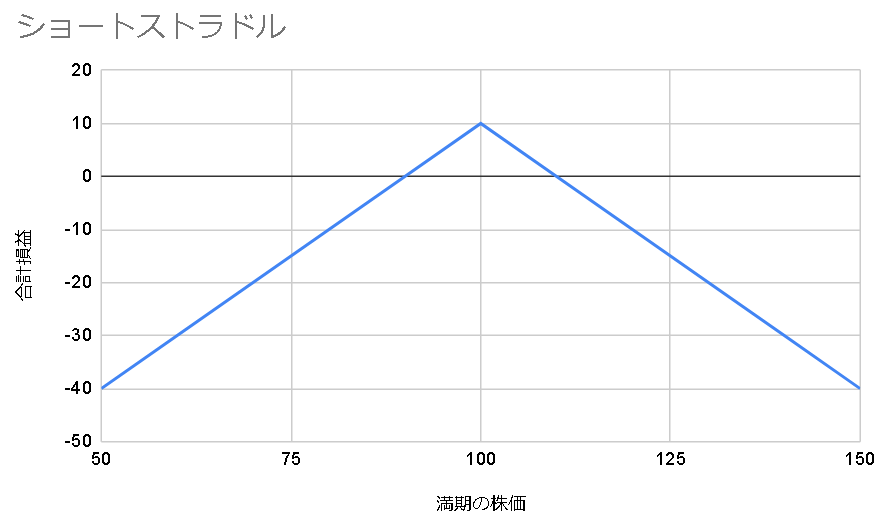
(行使価格100, CallとPutの価格5)

株価が上下に大きく動くと予想されるならロングストラドル、あまり動かないと予想するならショートストラドルが戦略として取れる。

もう少し深堀りすると、このストラドルを構成するCallとPutの価格(プレミアム)よりも株価が動くと予想した場合はロングストラドルを、動かないと予想した場合はショートストラドルが戦略として取れる。

株価の値動きの激しさはボラティリティとして計算・予測付けされており、市場のオプションが含んでいるボラティリティはインプライドボラティリティと呼ばれる。
つまりインプライドボラティリティが低く見積もられている場合はロングストラドル、高く見積もられている場合はショートストラドルを取ると儲けられる。

インプライドボラティリティを逆算的に見積もる方法としてBrenner and Subrahmanyamの公式がある。

ちょっと何書いてあるのかよく分からなかったけど、ストラドルのボラティリティは

C+P ≃ √(2/π)*σS√T

C+P:フォワード価格におけるストラドルのプレミアム, Call+Put
σ:インプライドボラティリティ
S:現在の株価
T:満期までの時間

σ ≃ (C+P)/S/√T =0.798...*(C+P)/S/√T

フォワード価格Fは将来の取引時に裁定取引が起きない、現在の株価Sと金利r(と配当D)から求められ

F=(S-D)e^rT

となる。

行使価格Kがフォワード価格Fと等しいとき、Put-Call Parityから

C-P = S-D-Ke^(-rT)
       = S-D-(S-D)e^rT*e(-rT)
       = 0

よってPutとCallのプレミアムが等しいときの行使価格KにおけるCallとPutの価格は

C=P=0.798...*(C+P)/S/√T/2
       =0.399...*(C+P)/S/√T

ロングストラドルの利益Rl, ショートストラドルの利益Rsの一般化

行使価格K, 満期の株価S, CallとPutのプレミアムの合計(C+P)を用いて

Rl = max(S-K-C, 0)+max(K-S-P, 0)
RIの最大値はS>K+(C+P)またはS<K-(C+P)のとき、Rl = |S-K|-O
最小値はK+(C+P)<S<K-(C+P)のとき、RI = -(C+P)

Rs = -max(S-K-C, 0)-max(K-S-P, 0)
Rsの最大値はK+(C+P)<S<K-(C+P)のとき、Rs = (C+P)
Rsの最小値はS<K+(C+P)またはS>K-(C+P)のとき、Rl = -|S-K|+O

損益分岐点はS = K+(C+P)またはS=K-(C+P)

ロングストラドルの損益 Rl = max(S-K-C, -C)+max(K-S-P, -P)
ショートストラドルの損益 Rs = -max(S-K-C, -C)-max(K-S-P, -P)
損益分岐点 S = K+(C+P) または S = K-(C+P)

もっと大きく動くか動かないかに賭ける、ストラングル

・行使価格が異なる
・満期までの時間が同じ
・CallとPutを1つずつ買う(ロングストラングル)または売る(ショートストラングル)

損益グラフは以下

(Callの行使価格110, Putの行使価格90, プレミアムはそれぞれ5)

現在の株価よりも高いCallと、現在の株価よりも低いPut(アウトオブザマネー)から成立する戦略。アウトオブザマネーのオプションを使うので

・ストラドルよりもプレミアムの合計が安い
・ストラドルより大きく値動きをしないとロングストラングルは利益を上げられない

といった特徴がある。

ロングストラングルの利益Rl, ショートストラングルの利益Rsの一般化

Callの行使価格Kc, プレミアムC, Putの行使価格Kp, プレミアムP, 満期の株価Sとする。

Rl = max(S-Kc-C, -C)+max(Kp-S-P, -P)
RIの最大値はS>Kc+(C+P)のときRI = S-Kc-(C+P)
またはS<Kp-(C+P)のときRI=Kp-S-(C+P)
RIの最小値はKp-(C+P)<S<Kc+(C+P)のときRI = -(C+P)

Rs = -max(S-Kc-C, -C)-max(Kp-S-P, -P)
Rsの最大値はKp-(C+P)<S<Kc+(C+P)のときRs = (C+P)
Rsの最小値はS>Kc+(C+P)のときRs = Kc-S+(C+P)
またはS<Kp-(C+P)のときRs = S-Kp+(C+P)

損益分岐点はS=Kc+OまたはS=Kp-O

ロングストラングルの損益 Rl = max(S-Kc-C, -C)+max(Kp-S-P, -P)
ショートストラングルの損益 Rs = -max(S-Kc-C, -C)-max(Kp-S-P, -P)
損益分岐点 S = Kc+(C+P) または S = Kp-(C+P)

お得にオプションを買おう、○○スプレッド

・満期までの時間が同じ
・Putを1つ買って1つ売る、またはCallを1つ買って1つ売る
1. 低い行使価格のCallを1つ買って、高い行使価格のCallを1つ売る(ロングコールスプレッド)
2. 低い行使価格のCallを1つ売って、高い行使価格のCallを1つ買う(ショートコールスプレッド)
3. 高い行使価格のPutを1つ買って、低い行使価格のPutを1つ売る(ロングプットスプレッド)
4. 高い行使価格のPutを1つ売って、低い行使価格のPutを1つ買う(ショートプットスプレッド)

まずはコールスプレッドについて、損益グラフは以下のようになる

行使価格90, プレミアム15と行使価格110, プレミアム3のCallを売買

ロングコールスプレッドは単純に行使価格90のCallを買うするよりも、行使価格が高いCallを売って得たお金を、行使価格が低いCallの購入代金にあてる戦略。ただし高い方の行使価格まで上がるとそれ以上の利益は見込めなくなる。
逆に低い行使価格以下になったとしても、それはそれで高い行使価格で売ったCallが行使されることはないので、満期に株価が高く行使価格以下であればお得に株をゲットである。

ショートコールスプレッドはその反対で、満期の株価が低い行使価格以上、損益分岐点以下だと儲け。後述するロングプットスプレッドと同じ。
ショートコールスプレッドを持っていると、ロングしている株がどれだけ下がっても一定の利益を見込める。上がるとちょっと損する。

ロングコールスプレッドの利益Rl, ショートコールスプレッドの利益Rsの一般化

Callの行使価格Kl<Kh, プレミアムCl, Ch, 満期の株価Sとする。

Rl = max(S-Kl-Cl, -Cl)-max(S-Kh-Ch, -Ch)
RIの最大値はS≧Kh-Chのとき、RI=Kh-Kl-(Cl-Ch)
RIの最小値はS≦Kl+Clのとき、RI=-(Cl-Ch)

Rs = -max(S-Kl-Cl, -Cl)+max(S-Kh-Ch, -Ch)
Rsの最大値はS≦Kl+Clのとき、Rs=(Cl-Ch)
Rsの最小値はS≧Kh-Chのとき、Rs=(Cl-Ch)-Kh+Kl

損益分岐点はKl+Cl<S<Kh-Chにあり、このときmax(S-Kl-Cl, -Cl)=S-Kl-Cl, max(S-Kh-Ch, -Ch)=-Ch
Rl = (S-Kl-Cl)-(Ch) = 0
S = Kl+(Cl-Ch)

ロングコールスプレッドの損益 Rl = max(S-Kl-Cl, -Cl)-max(S-Kh-Ch, -Ch)
ショートコールスプレッドの損益 Rs = -max(S-Kl-Cl, -Cl)+max(S-Kh-Ch, -Ch)
損益分岐点 S = Kl+(Cl-Ch)

プットスプレッドの損益グラフはコールスプレッドを逆にした形となる。

行使価格110, プレミアム15と行使価格90, プレミアム3のPutを売買

ロングプットスプレッドは満期の株価が低い行使価格以上、損益分岐点以下だと儲け。ショートコールストラドルと同じ。
ロングしている株がどれだけ下がっても一定の利益を見込める。上がるとちょっと損する。

逆にショートプットストラドルはロングコールスプレッドと同じ。

一般化も同じくロングプットスプレッドの利益Rl, ショートプットスプレッドの利益Rsの一般化

Putの行使価格Kh>Kl, プレミアムPh, Pl, 満期の株価Sとする。

Rl = max(Kh-S-Ph, -Ph)-max(Kl-S-Pl, -Pl)
RIの最大値はS≦Kl-Plのとき、Rl = Kh-Kl-(Ph-Pl)
Rlの最小値はS≧Kh+Phのとき、Rl = -(Ph-Pl)

Rs = -max(Kl-S-Ph, -Ph)+max(Kl-S-Pl, -Pl)
Rsの最大値はS≧Kh+Phのとき、Rs=(Ph-Pl)
Rsの最小値はS≦Kl-Plのとき、Rs=(Ph-Pl)-Kh+Kl

損益分岐点はKl-Pl<S<Kh+Phにあり、max(Kh-S-Ph, -Ph)=Kh-S-Ph, max(Kl-S-Pl, -Pl)=-Pl
Rl = Kh-S-Ph+Pl=0
S = Kh-(Ph-Pl)

ロングプットスプレッドの損益 Rl = max(Kh-S-Ph, -Ph)-max(Kl-S-Pl, -Pl)
ショートプットスプレッドの損益 Rs = -max(Kl-S-Ph, -Ph)+max(Kl-S-Pl, -Pl)
損益分岐点 S = Kh-(Ph-Pl)

ストラドルやストラングルの底なし損をカバー、バタフライ

・満期までの時間が同じ
・行使価格の高いオプションを1つ、低いオプションを1つ買い、中間のオプションを2つ売る(ロングバタフライ)
行使価格の高いオプションを1つ、低いオプションを1つ売り、中間のオプションを1つ買う(ショートバタフライ)

コールバタフライの損益グラフは以下のようになる。

行使価格90, プレミアム15－行使価格100, プレミアム7－行使価格110, プレミアム3
この戦略(スプレッド)を1つ買うためのプレミアムの合計は15+3-7x2=4

ロングバタフライはショートストラドルと比べて損がプレミアム額に限定されている。反対にショートバタフライは利益がプレミアム分に限定される。

プットバタフライはコールバタフライの逆となる。

コールバタフライの損益を一般化する。行使価格をKl<Km<Kh, プレミアムはCl, Cm, Chとする。プレミアムの合計はO=(Cl-2*Cm+Ch)である。

Rl = max(S-Kl-Cl, -Cl)-2*max(S-Km-Cm, -Cm)+max(S-Kh-Ch, -Ch)
RIの最大値はS=Kmのとき、RI=Km-Kl-O
RIの最小値はS≦Kl+OまたはS≧Kh-Oのとき、Rl = -O

Rs = -max(S-Kl-Cl, -Cl)+2*max(S-Km-Cm, -Cm)-max(S-Kh-Ch, -Ch)
Rsの最大値はS≦Kl+OまたはS≧Kh-Oのとき、Rs = O
Rsの最小値はS=Kmのとき、Rs=O-Km+Kl

損益分岐点はKl<S<KmとKm<S<Khの2点にある。
Kl+Cl<S<Kmのときmax(S-Kl-Cl, -Cl)=S-Kl-Cl, max(S-Km-Cm, -Cm)=-Cm, max(S-Kh-Ch, -Ch)=-Ch
Rl = (S-Kl-Cl)-2(-Cm)+(-Ch) = 0
S = Kl+O
Km<S<Kh+Chのときmax(S-Kl-Cl, -Cl)=S-Kl-Cl, max(S-Km-Cm, -Cm)=S-Km-Cm, max(S-Kh-Ch, -Ch)=-Ch
Rl = (S-Kl-Cl)-2(S-Km-Cm)+(-Ch)
    = -Kl-S+2Km-(Cl-2*Cm+Ch)
Km = (Kh+Kl)/2なので
-Kl-S+2Km-(Cl-2*Cm+Ch)
=  Kh-S-O=0
S = Kh-O

ロングコールバタフライの損益 Rl = max(S-Kl-Cl, -Cl)-2*max(S-Km-Cm, -Cm)+max(S-Kh-Ch, -Ch)
ショートコールバタフライの損益 Rs = -max(S-Kl-Cl, -Cl)+2*max(S-Km-Cm, -Cm)-max(S-Kh-Ch, -Ch)
損益分岐点 S = Kh-O, O=(Cl-2*Cm+Ch)

プットバタフライはコールバタフライの逆となるので省略。

格安で株を買いたい、バイライト

・現物の株を買う
・行使価格の高いCallを売る

損益グラフは以下のようになる。

株価100, 行使価格110, プレミアム5

市場では「バイライトを買う」場合、「コールを買って株を売る」という取引になる。

提示価格KのバイライトがマーケットでBid-Askがb-aで提示され、この取引では株価SとコールのプレミアムCについては任意の値となる。
行使価格Kのバイライトをマーケット価格aで買う場合、

a=C-(S-K)

を満たすように行使価格KでプレミアムCのコールを買い、同数の株をSで売る。
つまり「コールCを(S-K)よりいくら高く取引するか」という取引でもある。

損益を一般化していく。「バイライトを買う」場合の損益Rlは、初期の株価S0を使って

Rl = S0-S+max(S-K, 0)-C
Rlの最大値はS<Kのとき、Rl = S0-S-C
RIの最小値はS>Kのとき、RI = S0-K-C

「バイライトを売る」場合の損益Rsは

Rs = S-S0-max(S-K, 0)+C
Rsの最大値はS>Kのとき、Rs = K-S0+C
Rsの最小値はS<Kのとき、Rs = S-S0+C

損益分岐点はS=S0-C

バイライトを買った場合の損益 Rl = S0-S+max(S-K-C, -C)
バイライトを売った場合の損益 Rs = S-S0-max(S-K-C, -C)
損益分岐点 S=S0-C

株の値下げに備えたい、マリードプット

・現物の株を買う/売る
・Putを買う/売る
(株とPutで同じポジションを持つ)

損益グラフは以下のようになる

株価100, 行使価格90, プレミアム5

ロングマリードプット(現物の株を買ってPutも買う)は現物の株の下落に備えたポジションになる。
ショートマリードプットはロングプットスプレッドに対する優位性がちょっと分からないですね。

ロングマリードプットの損益 Rl = S-S0+max(K-S-P, -P)
ショートマリードプットの損益 Rs = -S+S0-max(K-S-P, -P)
損益分岐点 S = S0+P

リスクリバーサル

・同じ限月
・異なる行使価格
・Callを買ってPutを売る、またはCallを売ってPutを買う

例えば現物の株を持っていて、その下落に備えたPutを買うとき、行使価格の高いCallを売ることで支払うプレミアムの合計を抑えることができる。
損益グラフは以下のようになる。

Callの行使価格120, プレミアム3を売ってPutの行使価格90, プレミアム5を買う

・フラット部分の損益はプレミアムの合計
・Putの行使価格以下になれば儲け
・ショートしたCallは行使価格より高くなっても現物でヘッジできている

という強みがある。

行使価格KcのCallを売って、行使価格KpのPutを買ったリスクリバーサルの損益Rを一般化する。

R = max(Kp-S-P, -P)-max(S-Kc-C, -C)
右の斜線は R = S-Kc-(C-P)
左の斜線は R = Kp-S+(C-P)
フラットになる範囲はKp-P≦S≦Kc+C

Callを買ってPutを売るリスクリバーサルでは反対に

Callの行使価格110, プレミアム5を買ってPutの行使価格80, プレミアム3を売る

この戦略(スプレッド)を取る場合、原則的に株価が上昇した方が嬉しいが決めた価格以上に上昇しなければ乗らないという戦略になる。左斜線部になれば無限損失になるので注意。

一般化すると

R = max(S-Kc-C, -C)-max(Kp-S-P, -P)
右の斜線はR=S-Kc-(C-P)
左の斜線はR=Kp-S-(C-P)
フラットになる範囲はKp-P≦S≦Kc+C

先物と同じ、コンボ

・同じ限月
・同じ行使価格
・Callを買ってPutを売る

このポジションを数式で表現するとC-P

Put-Call Parityから C-P=S-Ke(-rT)-D

これが満期になると
i) S>Kのとき
左辺はCallが行使されPutは棄却され、行使価格Kで株Sを手に入れる。

ii) S<Kのとき
左辺はCallを棄却しPutが行使され、行使価格Kで株Sが手に入る。

つまり株価がどう動こうとも行使価格Kで現物株を購入するポジションになる。

配当額を予想して儲けよう、リバーサル・コンバージョン

・コンボ(先物)をロング
・現物株を売る

コンボは C-P=S-Ke(-rT)-D で表現できる。

行使価格から行使価格に対する今のお金の価値と配当を引いた差

 K(1-e^(-rT))-D = r/c

としたとき

C-P = S-K+r/c

r/c = (C-P)-(S-K)

この r/c をリバーサル・コンバージョンとし、コンボ(先物)をロングして株現物を売ったのと同じになる。
r/c は先物と現物との差になるので r/c > 0ならば先物を持つのに現物より多く必要ということで、現物を保有するためのコストともいえる。

r/c = K(1-e^(-rT))-D

より、配当が想定より少ないと儲かる(=リバーサル)。

逆にリバーサル・コンバージョンをショートすれば現物株を買ってコンボ(先物)をショートしたのと同じ。株価が配当分だけ減少するが配当が貰えるのでプラマイゼロ。配当額が想定より大きいと先物は市場予想以上に下落するので儲かる(=コンバージョン)。

裁定取引の機会のひとつ、ボックス

・行使価格の低いコンボをロング/ショート
・行使価格の高いコンボをショート/ロング

損益グラフは以下のようになる。

行使価格90のコンボをロング、行使価格110のコンボをショート、プレミアムはそれぞれ5

満期のボックスの価値Rb = Kh-Kl
金利による時間分減衰を考慮すると現在のボックスの価値Rb' = Rb*e(-rT)

ボックスはコンボの組み合わせだけでなく、コールスプレッドとプットスプレッドの組み合わせと理解することもできる。

・行使価格の高いコールの売りと低いコール買い
・行使価格の高いプットの買いと低いプット売り

つまり、ボックスの価格=コールスプレッドの価格＋プットスプレッドの価格

これら2つの価格が行使価格の差より大きいければボックスをショート、小さければボックスをロングする裁定取引の機会を得る。

時間を操れ、カレンダースプレッド

・異なる限月
・同じ行使価格

満期の近いオプションをショート＋満期の遠いオプションをロング＝カレンダースプレッドのロング
と呼ぶ。(オプションはCall, Putだけでなくストラドルも含む)
カレンダースプレッドは2つの期間のボラティリティをトレードすることに価値がある。

例として短期コールをショートし、長期のコールをロングするコールカレンダーのロングを考える。
オプションの価値、プレミアムはブラック・ショールズ式(別記事で導出)で表現することができる。

それぞれのプレミアムをグラフ化すると

青線:短期コールのプレミアム, 赤線;長期コールのプレミアム
行使価格100, 短期コールの満期までの期間0.25, 短期コールの満期までの期間0.5, 金利1%, ボラティリティ30%

コールカレンダーの価値はCl-Csで表現でき、時間経過に従って下のグラフのようになる。

短期コールの満期までの時間 青線>赤線>黄線

このグラフから見られる特徴は

・株価が行使価格に近いほどコールカレンダーの価値が高い
・短期の満期に近付くほど、コールカレンダーのプレミアムの最大値は高くなる

オプションの価値(プレミアム)はブラック・ショールズ式の他に

プレミアム = 本質的価値 + 時間的価値

と分解して考えることができる。

そうすると短期のコールは満期になると時間的価値は減り、本質的価値のみになる。

今回、短期のコールをショート、長期のコールをロングしているので、短期コールの満期では株価が行使価格以下になってほしい。ただし長期のコールのプレミアムが下がるのは損なので、短期コールが満期のときの株価は行使価格の方が嬉しい。

短期コールが満期を迎えると長期コールのロングのみ残るので、短期コール満期後は株価が上昇した方が嬉しい。

ボラティリティが高いほどオプションの価値(プレミアム)が上昇するのでボラティリティが高いほど嬉しいが、短期コールの満期では行使価格で留まっていて欲しいという状態である。

短期プットと長期プットの売買の組み合わせをプットカレンダーと呼ぶ。

それぞれのプットのプレミアムと、ロングプットカレンダーのプレミアムをグラフ化すると

短期プットの満期までの時間 青線>赤線>黄線

ロングプットカレンダーでもコールの時と同じく、株価が行使価格と等しいときにプレミアムが最大になり、短期プットの満期に近付くほどその最大値は高くなる。

短期ストラドルと長期ストラドルの売買の組み合わせをストラドルスワップと呼ぶ。

ストラドルは限月と行使価格が同じPutとCall両方を買う/売る戦略である。

ストラドルのロングは株価が大きなボラティリティを持って動いた方がいい戦略だったが、ストラドルスワップが発動している間は株価が行使価格から動かない方がいい。

ストラドルスワップのロングは短期ではボラティリティ小→長期ではボラティリティ大となるボラティリティの差をトレードする戦略ともいえる。
ショートはその逆で、短期はボラティリティ大→長期はボラティリティ小となってほしい。

コンボを組み合わせろ、ジェリーロール

・満期の近いコンボを売る/買う
・満期の遠いコンボを買う/売る

コンボ＝同じ限月、同じ行使価格のCall買いPut売りまたはCall売りPut買い、先物と同じポジション。

コンボは C-P = S-K+r/c で表現できるので、株価と行使価格の差は限月の遠近に関係しないので、リバーサル・コンバージョン r/cだけが限月の違うコンボの差になる。

短期のコンボのr/c(1)と長期のコンボのr/c(2)とおけば、ジェリーロールのロングは

-r/c(1)+r/c(2)

r/cは現物を持つためのコストとと言えるので、短期で現物を持つコストと長期で現物を持つコストをやり取りするのがジェリーロールともいえる。

ではr/cの価格決定・変動要因とは、元々の式を見ると

r/c = K(1-e^(-rT))-D

から金利rと配当Dが変数なのが分かる。

・金利rが上昇する → r/cが上昇
・配当Dが上昇する → r/cが低下

ということは、ジェリーロールのロングは

・短期では金利が低下もしくは配当が上昇
・長期では金利が上昇または配当が低下

してくれると嬉しい。

他にもどんな戦略の組み合わせができるのか、考えてみよう！