Uniswap v3を完全に理解した

Uniswap v3ではwhitepaperにある式2.2に沿ってx, yの2つのトークンの量が変化する。

https://uniswap.org/whitepaper-v3.pdf

最終目標:①depositした資金は価格が動くとどのように変動するのか、②また現物をHODLしていた場合との差, 損失はどのくらいになるのか、depositする資産額と価格レンジの最小値、最大値を使って計算・予測できるようにする。

1) 式2.2の導出

2つのトークンx, yに対してUniswapはxy=kが成立するとしている。

このとき2つのトークンは、yをxで評価した価格Pを使って

y/x=P
y=Px

と書ける。

(例えばx=ETH, y=DAIとして, x=1, y=1800なら価格P=1800)

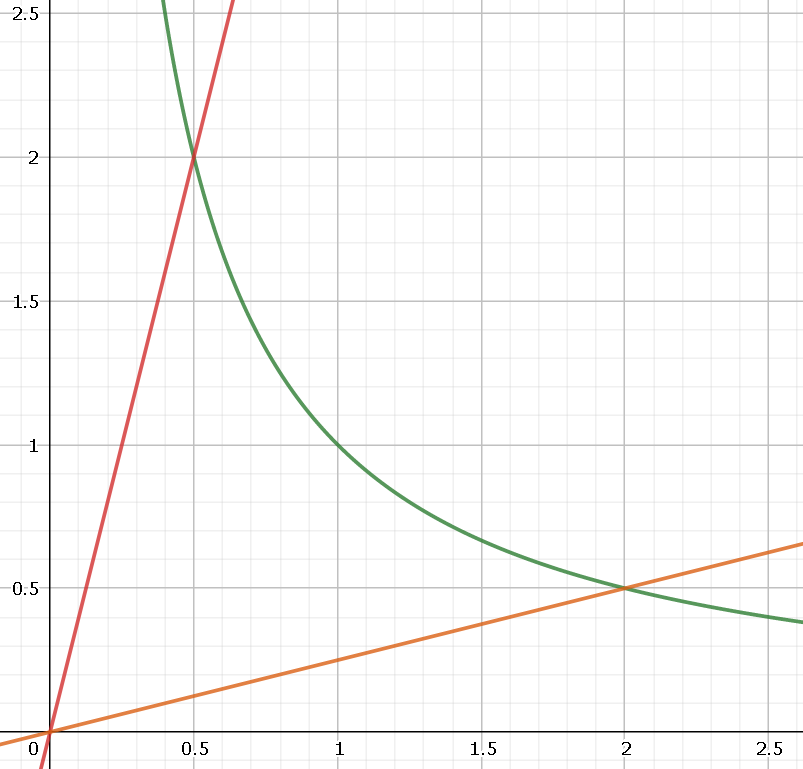
y=Pxとxy=kとの交点が価格Pに対してxy=kのプールが持つxとyの数である。

この交点のx,yをk, Pで表現すると下のように書ける。

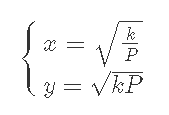
今回、取引する価格帯の下限の価格をPmin, 上限の価格をPmaxとすると、それぞれのx, y座標を表現できる。

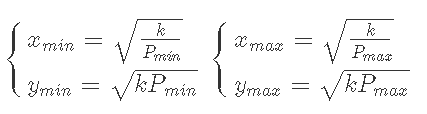
この価格より大きくなったり小さくなったときにxまたはyが0になるようにxy=kの式をx軸、y軸に対して平行移動するとする。

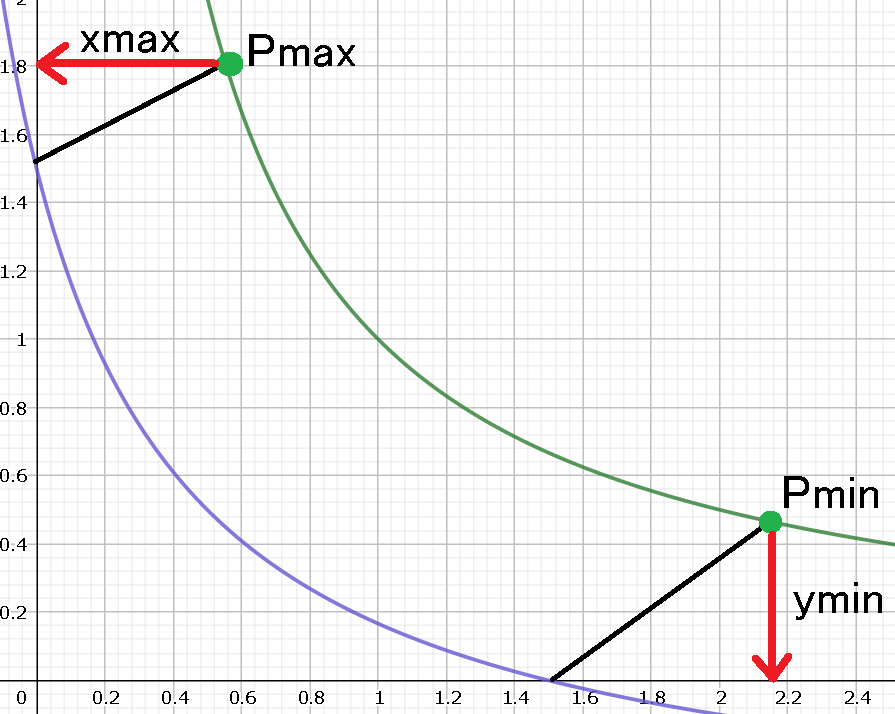
つまりxy=kの式をx軸方向にxmax, y軸方向にyminだけ平行移動した式である。

(x+xmax)(y+ymin)=k

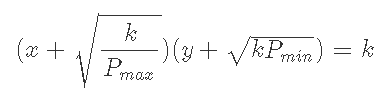
kの平方根をLとすると

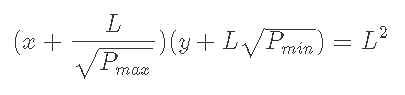
式2.2が導出される。

中学生でもできますね

2) 平行移動後の価格Pにおけるx, yをPmin, Pmax, P, Lで表現する

元々のxy=kの式が平行移動したので、価格Pも平行移動させます。

平行移動後の価格Pにおけるx, yは、点の平行移動なので

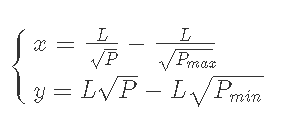
と表現できる。

筆者はバカなのでy=Pxを平行移動させて交点をわざわざ計算しました。

なお、これが成立するのはPmin≦P≦Pmaxのときのみ。

またこの範囲で2つのトークンの価値が釣り合っているときの価格Pmidを求めると,

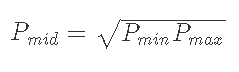
範囲の最大値と最小値の幾何平均となる.

3) P<Pmin, Pmax<Pのときのx, yについて考える

3-1) P<Pminのとき, y=0となる.

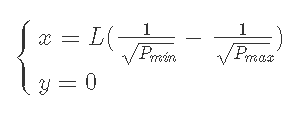
3-2) P>Pmaxのとき, x=0となる.

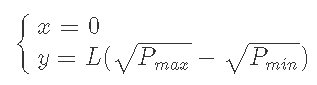
4) 自分のポートフォリオを知る

自分のLPにdepositした資産ωが現在価格Pに対してどのように変化するのか見ていきます。

yで評価した時の資産は下の式で表現できる.

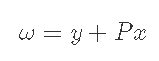
4-1) P<Pmin のとき, 全財産はxになっている.

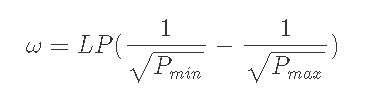
4-2) P>Pmaxのとき, 全財産はyになっている.

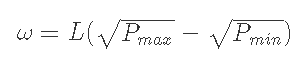
4-3) Pmin<P<Pmaxのとき

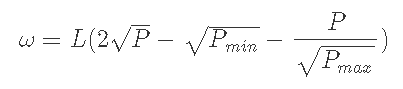
5) Lとは何か、初期deposit資産ω0, Pmin, Pmaxおよびdepositするときの価格Piから求める

これもPiがPmin~Pmaxの範囲に対して外側にあるか内側にあるかで異なる.

というのも範囲外から始める流動性提供は片側の流動性提供となるので, 実質的なPiは範囲の境界値で決定されるため.

式2.2(WP)および4)で求めた式を変形することでω0, PiのときのLを求めることができる.

5-1) Pi<Pminのとき, xのみdepositする.

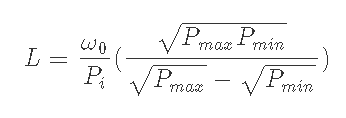
5-2) Pmax<Piのとき, yつまりω0のみdepositする.

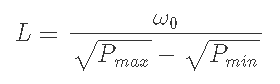
5-3) Pmin<Pi<Pmaxのとき

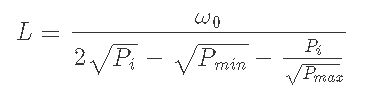
6) 最終目標①depositした資金は価格が動くとどのように変動するのか.

4)で求めた式に5)の式を適用することで任意の価格に対する現在の資産の評価額が求められる.

deposit時の価格PiがPi<Pmin, Pmin<Pi<Pmax, Pmax<Piの3通りと, 現在価格PがP<Pmin, Pmin<P<Pmax, Pmax<Pの3通りの合計9通りの表現が存在しうる.

単純に5)で求めたそれぞれのPiの状態に対するLを4)で示したPで表現される資産評価額ωの式に代入すればいい. 見た目が冴えないのが課題 シミュレータを考える時はLを分岐付けて計算してまとめておくと見栄えがいい.

6-1-1) Pi<Pmin, P<Pminのとき

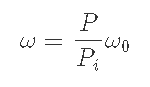
6-1-2) Pi<Pmin, Pmax<Pのとき

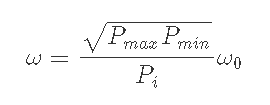
6-1-3) Pi<Pmin, Pmin<P<Pmaxのとき

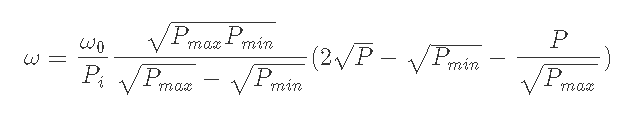
6-2-1) Pmax<Pi, P<Pminのとき

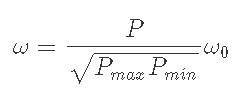
6-2-2) Pmax<Pi, Pmax<Pのとき

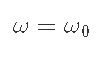
6-2-3) Pmax<Pi, Pmin<P<Pmaxのとき

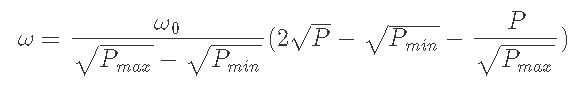
6-3-1) Pmin<Pi<Pmax, P<Pmin のとき

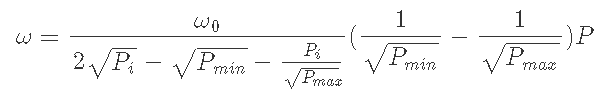
6-3-2) Pmin<Pi<Pmax, Pmax<Pのとき

6-3-3) Pmin<Pi<Pmax, Pmin<P<Pmaxのとき

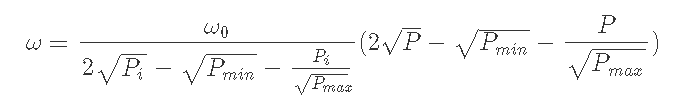
7) 最終目標②また現物をHODLしていた場合との差, 損失(impermanent loss)はどのくらいになるのか.

Impermanent Lossは定義から, v3にある資産の評価額ωv3とHODLしていたときの資産評価額ωHODLを使って, 以下の式で求められる

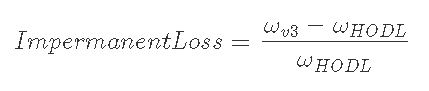
depositしたときのポートフォリオ, x, yが価格Pによってどのように変化するのか分かれば, 6)で求めたdepositした資産評価額との比較でImpermanent Lossを求めることができる.

以下で一応整理した式を記載しておくが, 定義の式に代入して個人的な美学で変形しただけであり, その式の形は本質を明示していないこともある.

ということで, Pi<Pmin, Pi>Pmax, Pmin<Pi<Pmaxのときの初期のポートフォリオを求め, それぞれからImpermanent lossを計算する.

7-1) Pi<Pminのとき, xのみdepositするのでポートフォリオはxのみ.

このときのx, ωHODLは

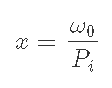
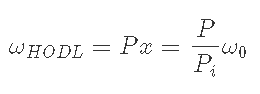
7-1-1) Pi<Pmin, P<Pminのとき

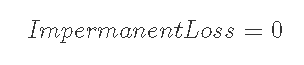
7-1-2) Pi<Pmin, Pmax<Pのとき

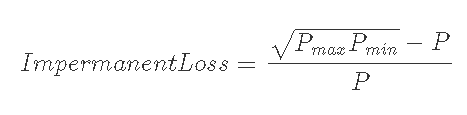
7-1-3) Pi<Pmin, Pmin<P<Pmaxのとき

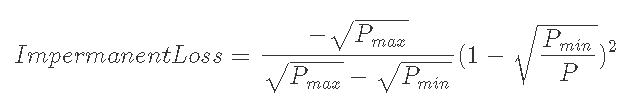
いずれにおいてもIL≦0

7-2) Pmax<Piのとき, yのみdepositするのでポートフォリオはyのみ, つまりω0.

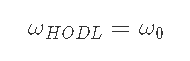
7-2-1) Pmax<Pi, P<Pminのとき

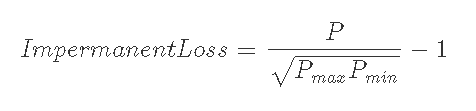
7-2-2) Pmax<Pi, Pmax<Pのとき

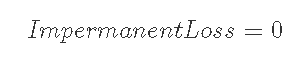
7-2-3) Pmax<Pi, Pmin<P<Pmaxのとき

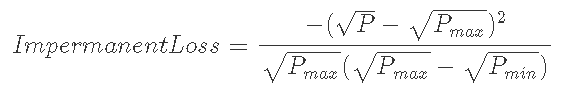
いずれにおいてもIL≦0

7-3) Pmin<Pi<Pmaxのとき、depositするx, yは2)と5)から求められる

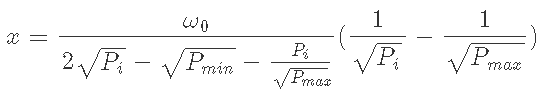
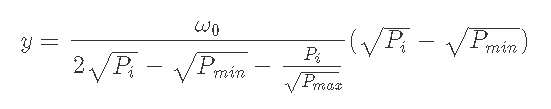
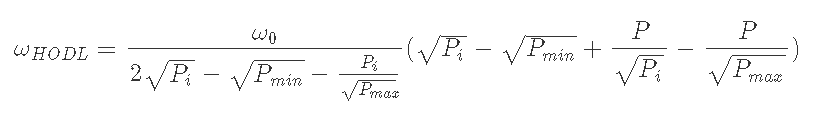
以下の式は、Supporting Infromationで示した式の方がきれいかもしれない。

7-3-1) Pmin<Pi<Pmax, P<Pminのとき

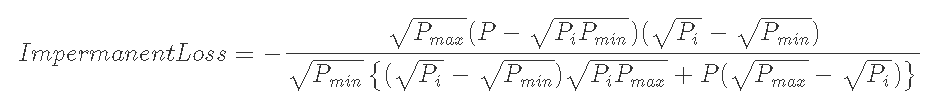
7-3-2) Pmin<Pi<Pmax, Pmax<Pのとき

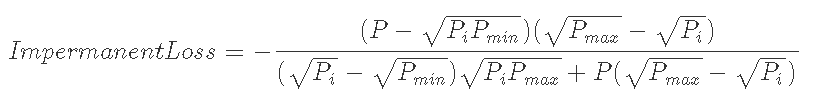
7-3-3) Pmin<Pi<Pmax, Pmin<P<Pmaxのとき

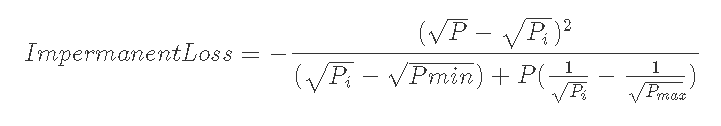
いずれにおいてもIL≦0

定義の式に代入して個人的な美学で変形しただけであり, その式の形は本質を明示していないこともある、大事なことなので。

8) それぞれのパターンにおけるILのグラフを示しておく

7) までの式を抽象度を高めるため, depositするときの相場価格Piに対して, 現在価格P=rPiと置き、変動率rとILの関係曲線を示す。気が向いたら各自rおよびPmax=MPi, Pmin=mPiと置いたときのM, mを使って7)の式を変形してみてほしい.

また、ポートフォリオ内の2つのトークンの価値が50:50になっている点は前にPmidで表現した.

1) PmidとPiが等しいとき

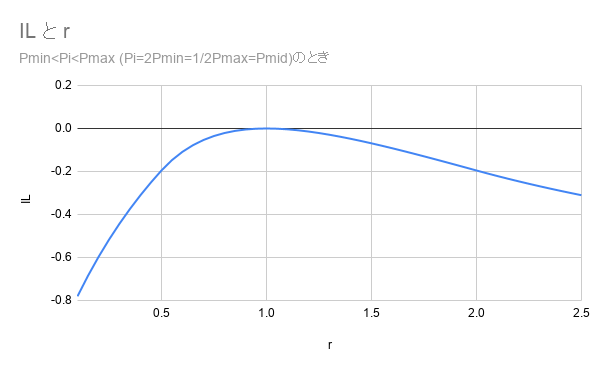
2) Pmid<Pi<Pmaxのとき

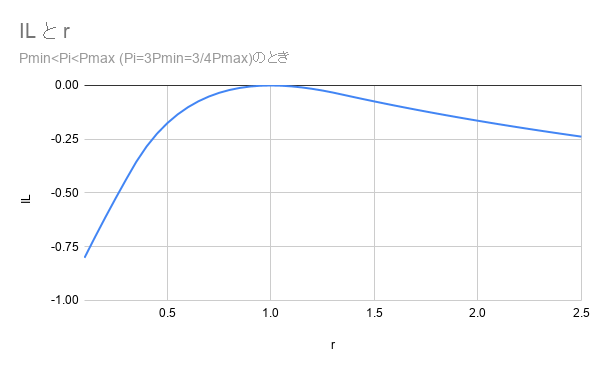
3) Pmin<Pi<Pmidのとき

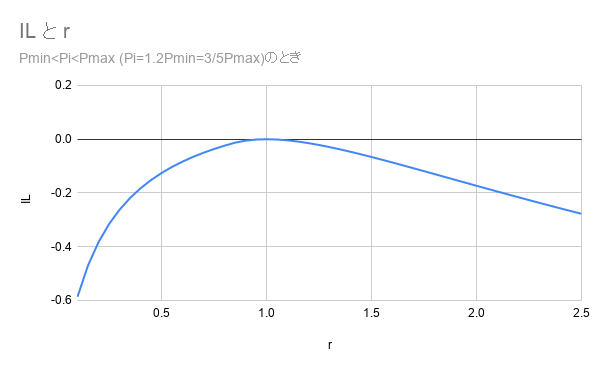
4) Pi<Pminのとき

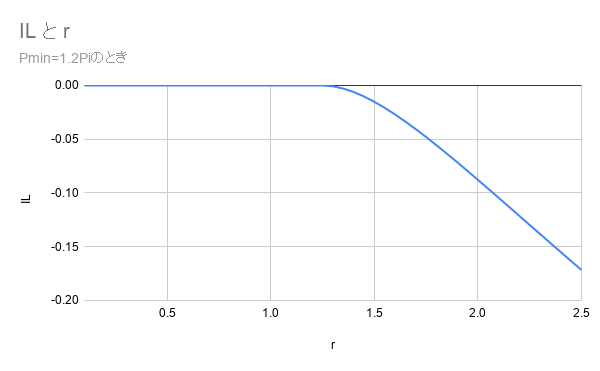
5) Pi>Pmaxのとき

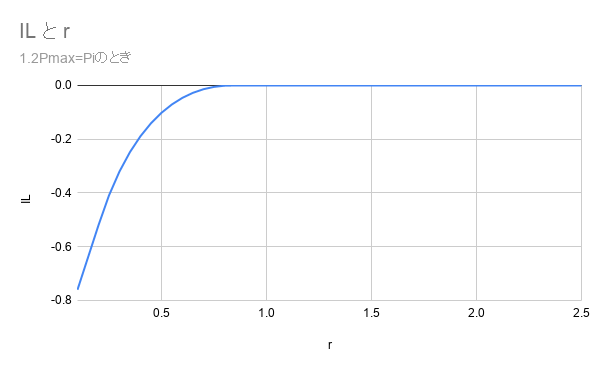
(Pi=任意の値, Pmin=500, Pmax=2000, Pmid=1000で描写)

9) 資金効率が何倍になるかを考える

ロックされてある資産額がfee収入の計算に使われるため, v2と比べてv3では何倍相当になったかを求めればいい.

Pmidにおけるv3の資産ωv3とv2における資産ωv2を比較する.

Pmidにおけるv3の資産ωv3をv2の形で評価すると以下のようになる.

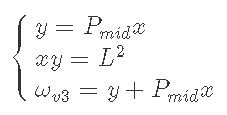
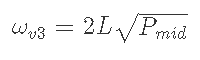
同じくv2のときの資産ωv2を、kを使って表現すると下のようになる.

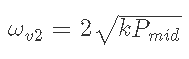
よってこれらの比は

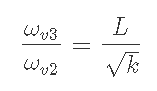
おまけ:シミュレータ