オプションを勉強するよ その4 グリークを理解してポジションの大きさ・リスク・取引を深く理解しよう Part.1

オプションの価値 Oを決定する要因として

・行使価格 K
・株の現物価格 S
・満期までの時間 T
・ボラティリティ σ
・配当 D
・金利 r

がある。それぞれが変化した時にオプションの価値がどう変化するのかの変化量や変化量の変化量をグリークと呼ぶ。

手持ちのオプションがこれら要因でどのように変化していくのか、グリークを理解してリスクを分析しよう。

デルタδ -株価Sが動くときのオプションの価値Oの動き-

δ= ∂O/∂S

構造的にデルタはディープインザマネーでは1、ファーアウトザマネーでは0になる。

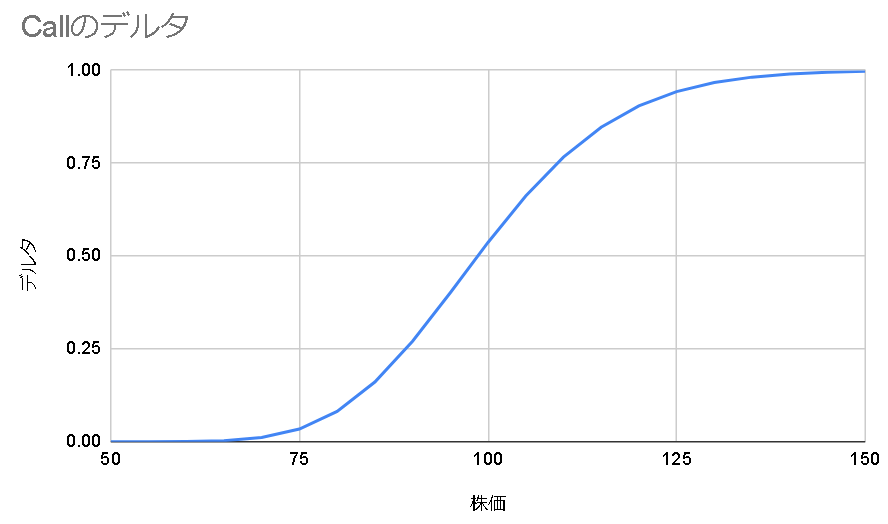
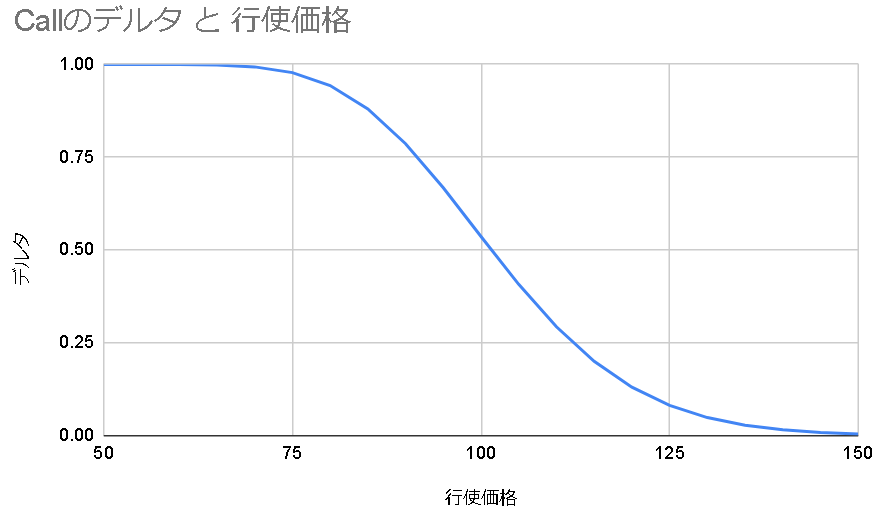
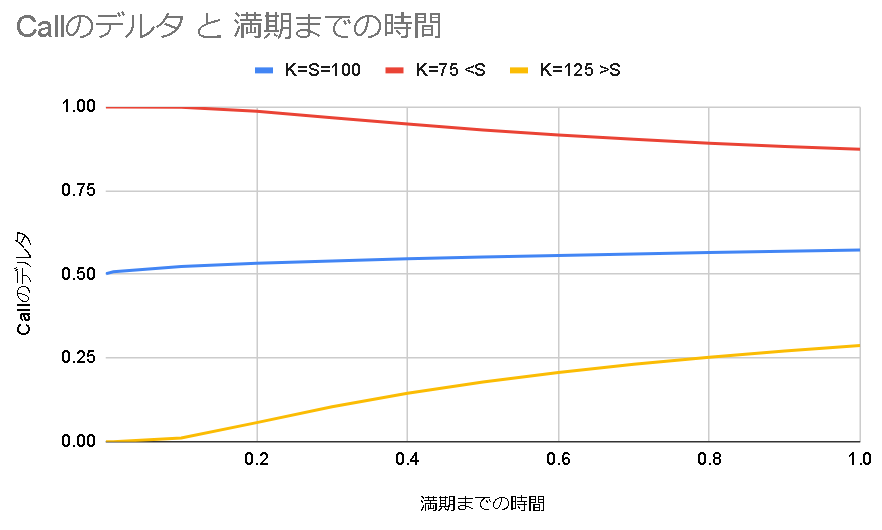
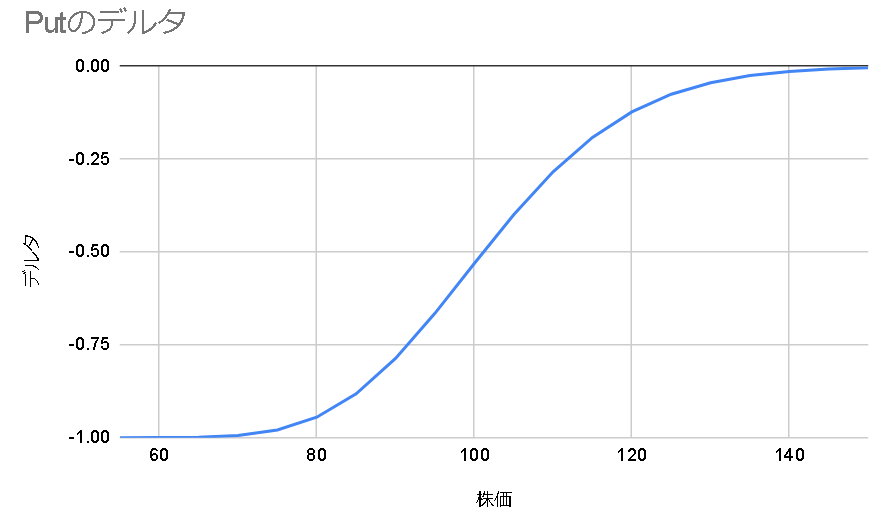
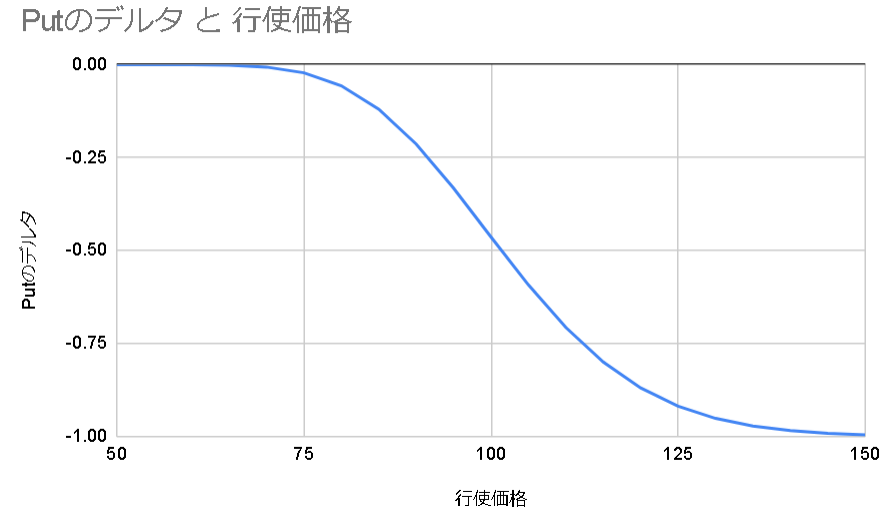
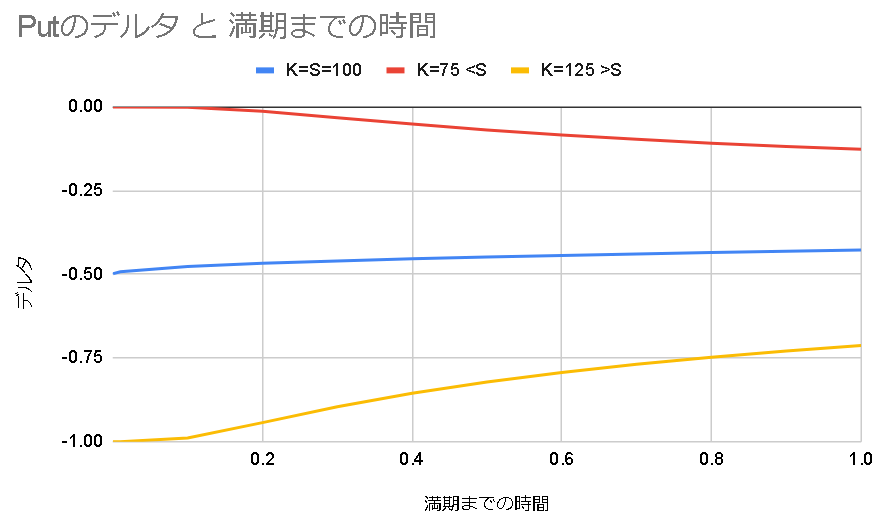
(株価100, 行使価格100, 満期までの時間0.25, ボラティリティ30%, 配当0, 金利1%)

デルタはオプションが行使できる確率と考えることもできる。

またヘッジ(ポートフォリオを無リスク状態)するために必要な株の枚数でもある。

ガンマγ -株価Sが動くときのデルタδの動き-

γ= ∂δ/∂S = ∂^2O/∂S^2

デルタは株価が動いたときにヘッジするために必要な株の枚数ならば、それが株価によってどのように変化していくのかを解析したのがガンマにあたる。

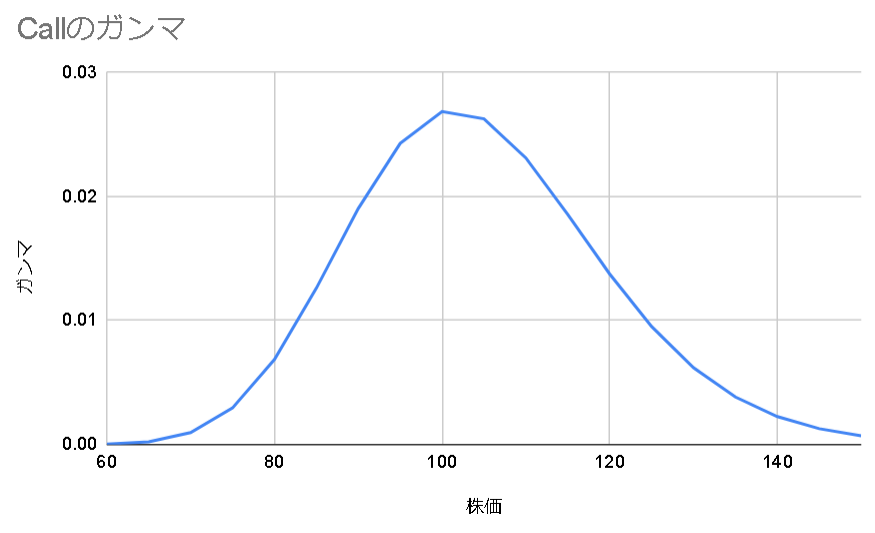
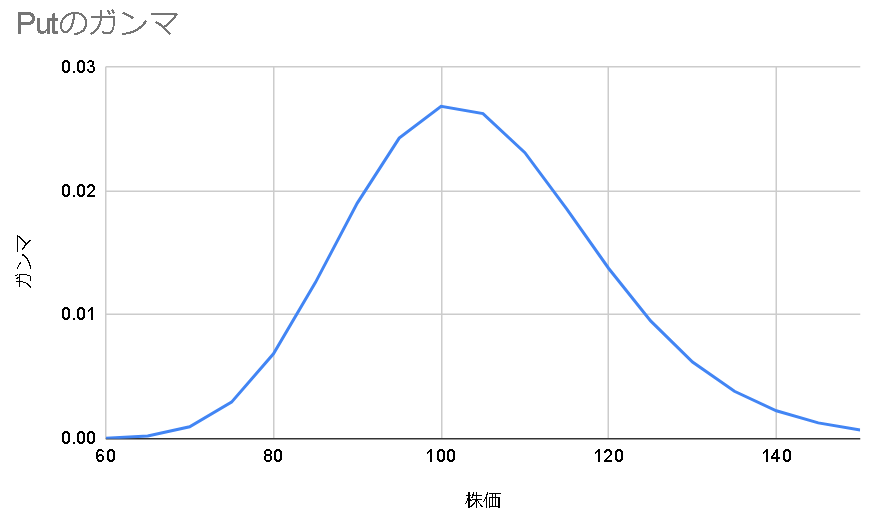
ガンマはデルタの傾きになるのでCallもPutも同じ値になるし、正の値を取る。

株価SがΔSだけ動いたとき、オプションのプレミアムの変化量デルタδはδ+γΔSと変化する。このときの平均デルタは

{δ+(δ+γΔS)}/2=δ+(γΔS)/2

となる。デルタの増減は

{δ+(γΔS)/2}*ΔS

オプションのプレミアムの変化をヘッジするために取った株の増減は

-δ*ΔS

そこでデルタの増減は

{δ+(γΔS)/2}*ΔS-δ*ΔS={γ(ΔS)^2}/2

で常にプラスの値を取る。つまりオプションとヘッジポジションを持てば、株価がどう動いても確実に利益を得られる算段になる。

実際にはそんな美味い話はなく、次のセクションで解説するセータθ(時間経過によるプレミアムの変化)が効いて差し引きになる。
またセータの意味から、ガンマは時間経過による株価変動におけるプレミアムの変化の期待値ともいえる。

他の構成要素とガンマとの関係も見ていく。

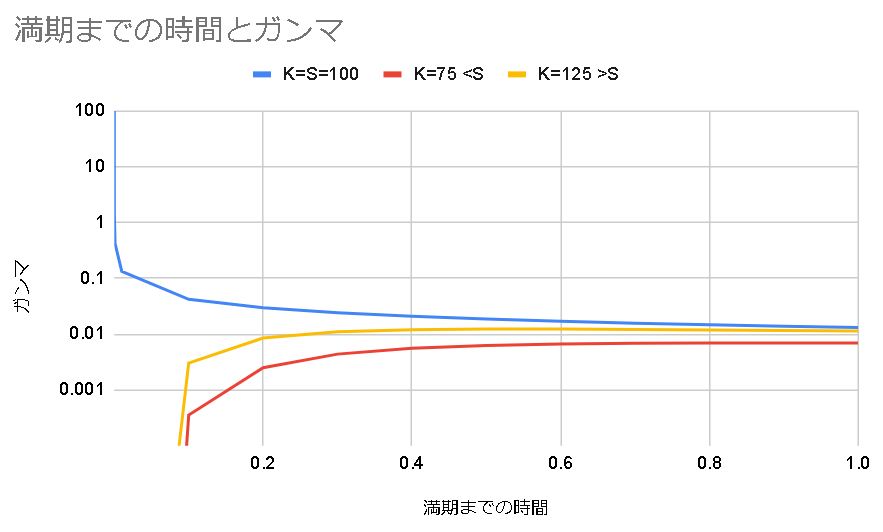
満期までの時間が短くなるほど

・株価Sと行使価格Kが等しいオプションのガンマは増大する

・株価Sと行使価格Kが離れているオプションのガンマは減少する

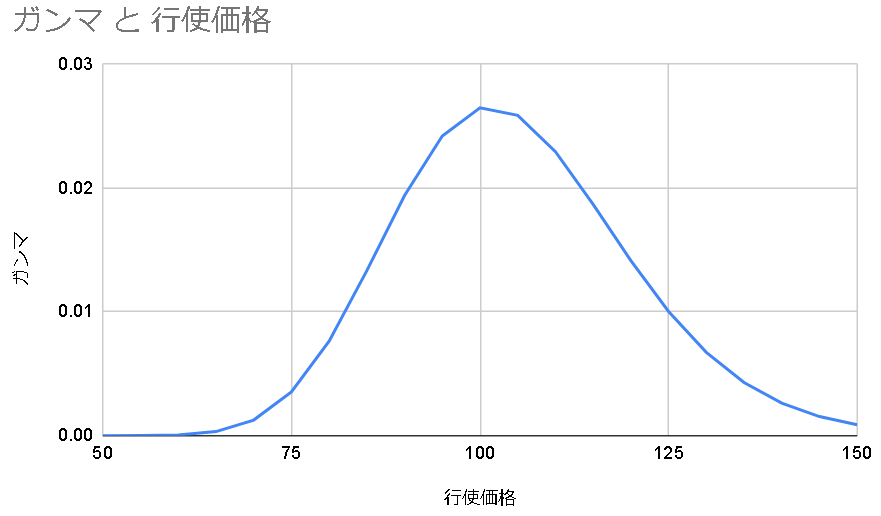
ガンマが最大となる行使価格Kは

K=S*e^(r+(σ^2)/2)T

行使価格が株価よりちょっとだけ大きいときにガンマは最大値を取る。

セータθ -時間Tが経過するごとのオプションの価値Oの動き-

θ= ∂O/∂t

オプションの価値 = 本質的価値 + 時間的価値 と分解した時、時間が経過するたびに時間的価値が低下し、オプションの価値が本質的価値のみに近くなる。
そこで時間に対するオプションの価値の変動をセータθで表現している。

セータはガンマと表裏の関係にあり、1日に動く株価に対する期待料のようなものである。

セータと株価・行使価格・時間の関係を見る。

コールにおいては

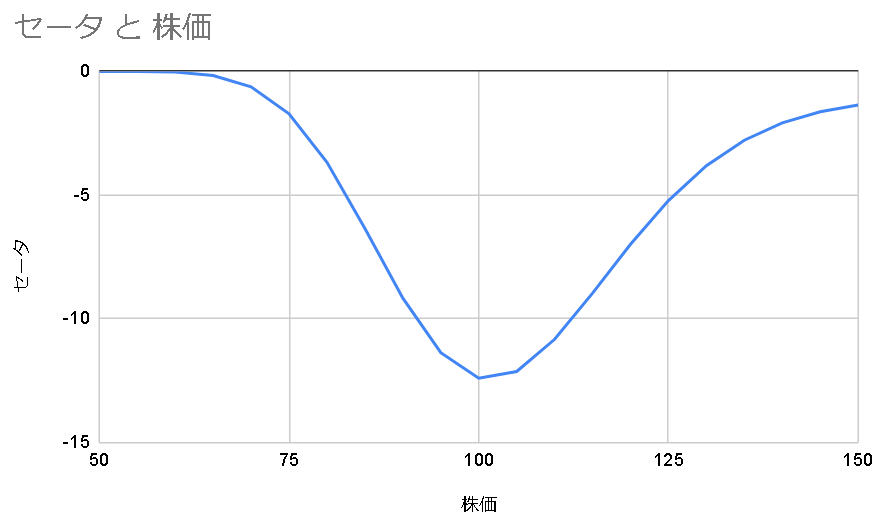
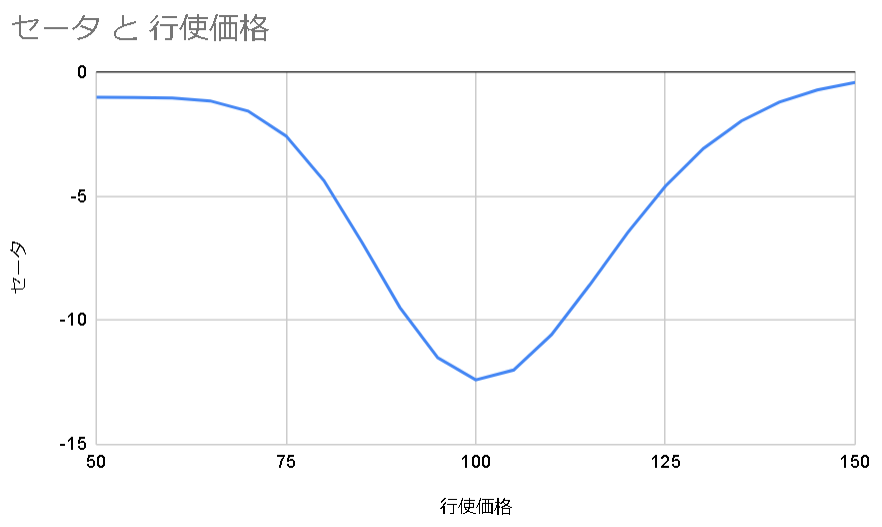
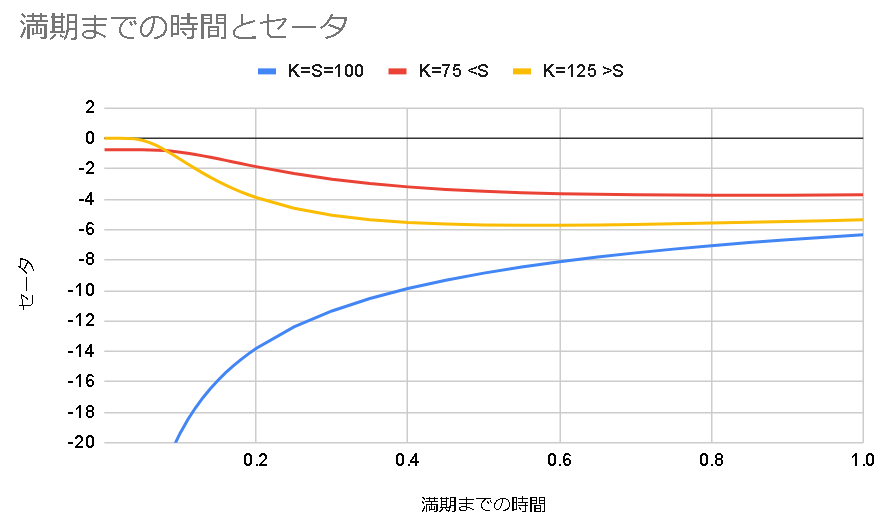
グラフの通り、セータは基本的に負の値を取る。前述したようにオプションの価値(プレミアム)は

プレミアム = 本質的価値 + 時間的価値

と分けることができる。時間が経過するたびにプレミアムは減少していく。

時間Tにおける株価Sの動きΔSの期待値はボラティリティσで表現できる。

ΔS = Sσ√T

このときのデルタδはガンマγを使うと δ+γΔS

平均のデルタは前述したように δ+(γΔS)/2

オプションとヘッジによるポジションの損益は (ΔS^2)γ/2

時間的価値はこの分だけ減少していく。

オプション取引の画面で表示されるボラティリティσは予想した値となるので、実際に時間経過で起きたボラティリティとは異なる。
実際のボラティリティが取引したオプションのボラティリティより大きければ、オプションをロングしていた側の勝ち。予想の範囲内であればショートしていた側の勝ちとなる。

プットのセータを図示する。

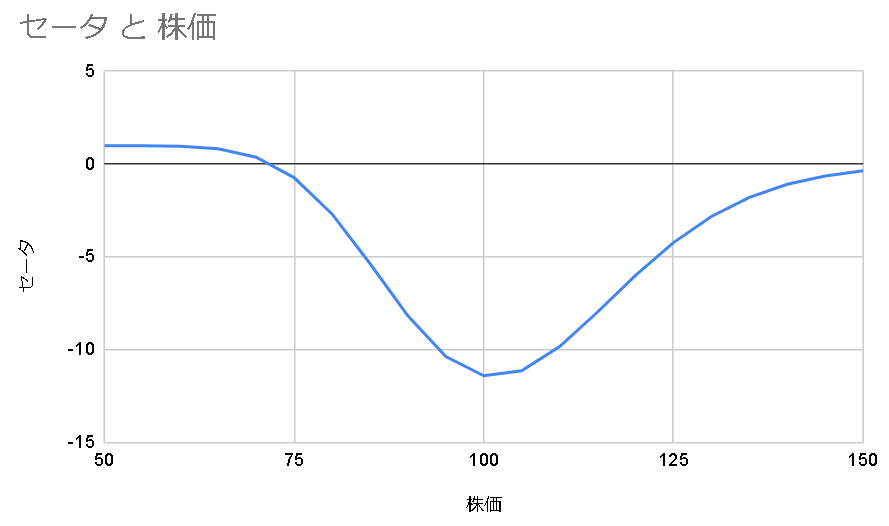
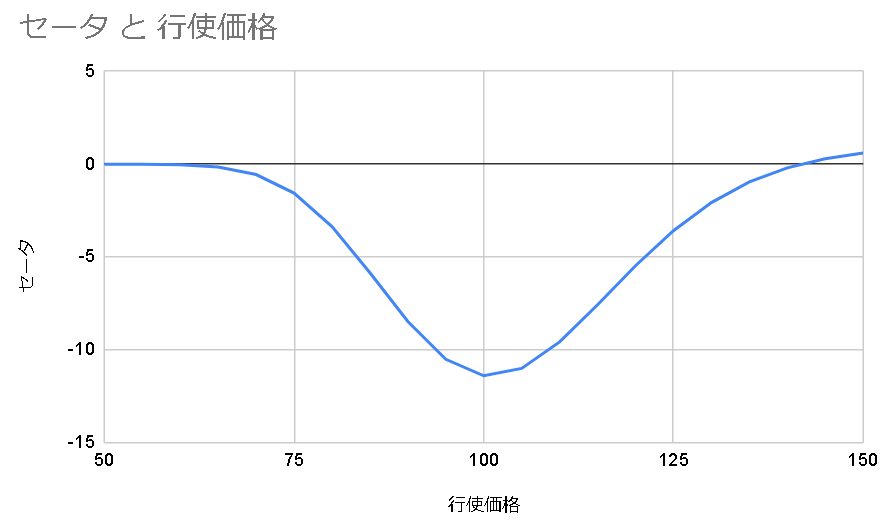
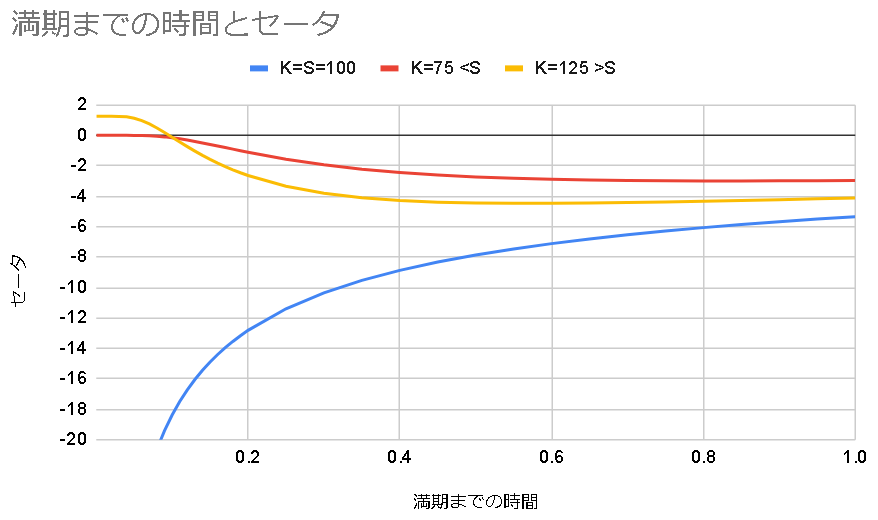
プットでもコールと同じくだいたいセータはマイナスとなる。

ベガV -ボラティリティσが動くときのプレミアムOの動き-

V = ∂O/∂σ

ボラティリティが大きいほどオプションの価値は高くなるのでベガは常に正の値になる。

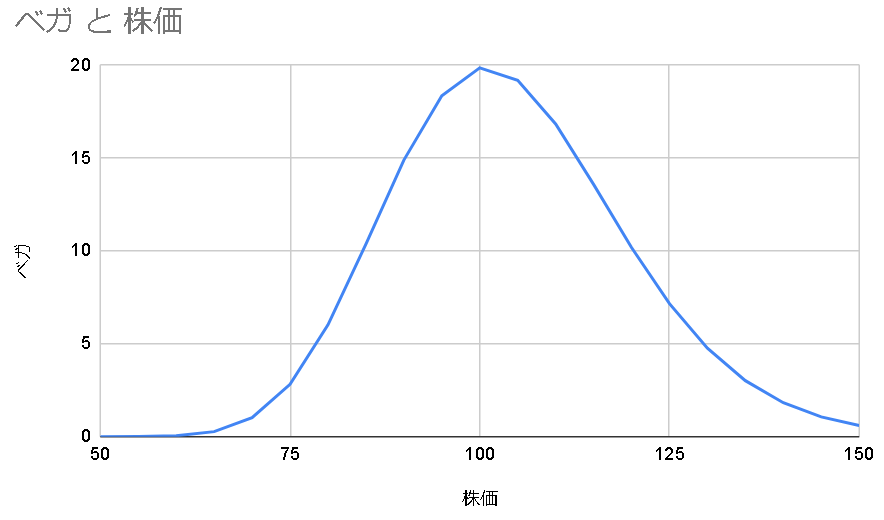
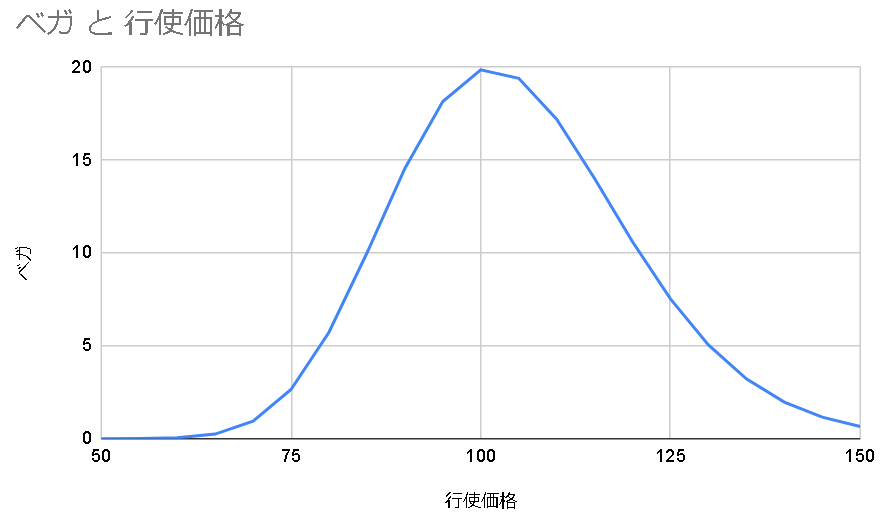
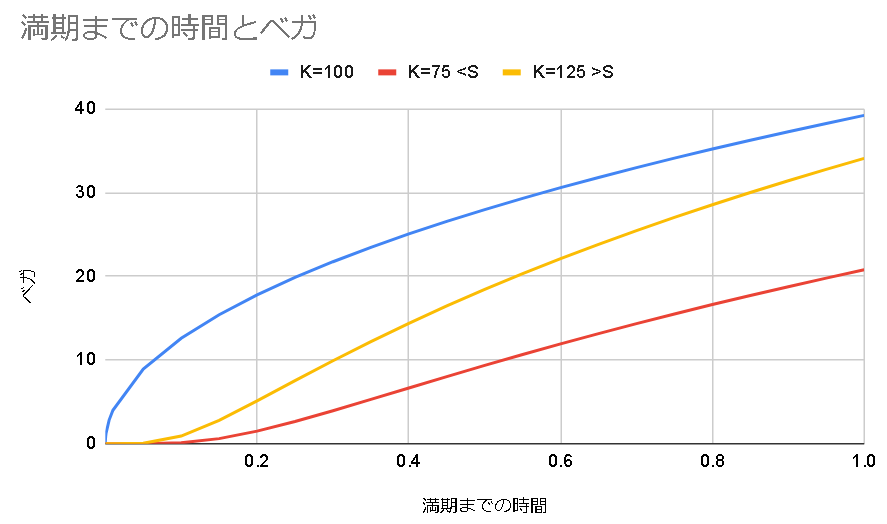
満期までの時間が長いほどボラティリティが上昇すると嬉しい。

ローρ -金利rが動くときのオプションの価値Oの動き-

ρ = ∂O/∂r

金利が大きくなれば株価が上昇するのでコールの価値は上昇し、プットの価値は減少する。

金利の動きは株価変動とボラティリティの上昇を生むため、他の構成要素が動かず金利だけ動くような状況はほぼありえない。もっと難しいことを勉強することになったら学び直そう。

イプシロンε(プサイψ) -配当Sの動きに対するオプションの価値Oの動き-

配当利回りをqとおくと

ε = ψ = ∂O/∂q

配当が増えれば株価が下がるのでコールの価値は減少し、プットの価値は上昇する。
配当額だけ株価が減少すると考えると、デルタδで解釈することができる。

アメリカンオプションでは金利と配当の関係で早期行使する選択があるため、より複雑になる。