【python】マークルツリーを作ってみた

●著者

がくしです。

●目的

マークルツリーを理解するにあたって、プログラミングができるなら日本語よりコード読んだほうが早いだろうと思い、実際に作ってみました。

●概略

マークルツリーとは、データ群の要約を作成し、要約と元データの整合性を見ることで、改ざんが行われてないか検証をする技術です。その際に、データ群の一部のみを知ってるだけで、検証が可能な事がポイントとなります。

この仕組みは、walletを使う際に役立っています。walletがブロックチェーン上の全てのトランザクションデータを持つと重くなってしまうので、代わりに要約されたデータだけを持っています。しかしそれだけだと、トランザクションデータが見れないので、自身のアドレスの残高を参照することが出来ません。そこで、自身のアドレスのみを使って改ざんの有無を検証した上で、元データから自身のトランザクションデータを取得します。

●図解

サトシ・ナカモトの論文の図がわかりやすいです。

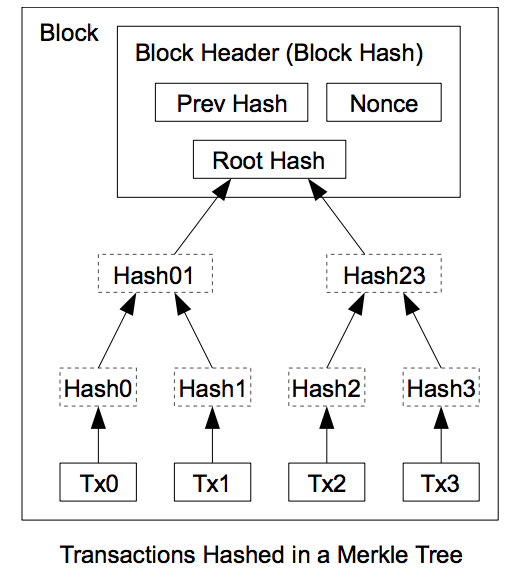
マークルツリーの概要です。各Txがトランザクションを表しています。それぞれのハッシュ値を連結したものを更にハッシュ化する事を繰り返し、Root Hash(マークルルート)を算出します。トランザクションからマークルルートに至るツリー構造を、マークルツリーと呼びます。また、マークルルートを含むブロックの要約（Block Header)のみを、walletは保持します。

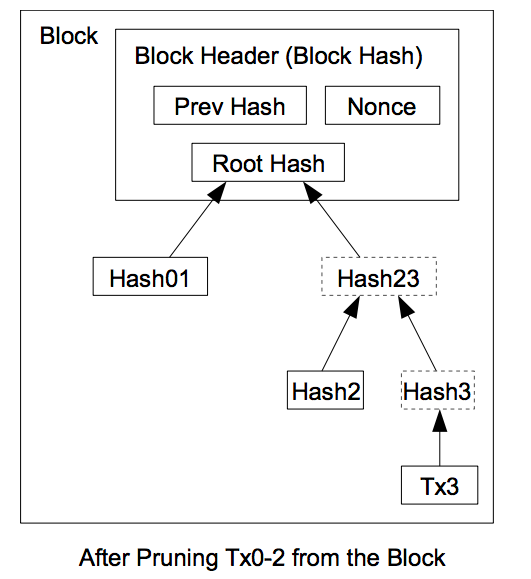
マークルパスの概要です。マークルルートは、全てのトランザクションを知らなくても算出できます。図のように、Tx3/Hash2/Hash01の値だけで、マークルルートを算出できます。この算出に必要な最低限の値を、マークルパスと呼びます。マークルパスから算出したハッシュ値と、walletが既に持っているハッシュ値が一致することが、改ざんが行われていないことの証明となります。

●コード全文

まず全体をざっくり見てみましょう。

詳細は後述するので、雰囲気だけ見てください。

・Nodeクラス
・Treeクラス
・caluculator関数

の、3つから構成されています。

それぞれ見ていきましょう。

●Nodeクラス

【プロパティ】

・left       ：子ノード（左）
・right     ：子ノード（右）
・parent  ：親ノード
・sibling  ：兄弟ノード
・position：兄弟ノードとの位置関係
・data     ：元のデータ
・hash     ：ハッシュ値

・left/right/parent

親ノードと子ノードを格納しています。各ノードが親子関係のデータを持つことで、ツリー上の構造を表現します。

・sibling/position

siblingは、共通の親を持つ隣のノードです。positionは、siblingとの位置関係で、leftかrightの文字列を格納します。これらは、マークルパス作成時に使います。

・data/hash

保管したいデータと、それのハッシュ値です。ここではsha256関数を使ってハッシュ化してます。

●Treeクラス

【プロパティ】

・leaves：ツリーの末端のノード
・layer  ：現在の最上層のノード集
・root   ：マークルルート

・leaves

最下層のノード群です。元データを格納してるので、後述するsearchメソッドで使います。

・layer

ツリーを作成する最中の、最上層のノード群です。こちらはbuild_layerメソッドで使います。

・root

マークルルートです。

【メソッド】

・__init__     :初期化
・build_layer：layerを一つ上の階層のものに上書き
・build_tree ：tree全体の作成
・search      ：所望のデータを格納するnodeの検索
・get_pass   ：マークルパスの作成

・__init__

文字列のリストとして受け取ったデータ群を、ノードのリストに変換してleavesに格納しています。また、そのleavesが最初の層になるので、コピーしたものをlayerに格納しています。

・build_layer

現在の最上層であるlayerの一個上の層をnew_layerとして作成し、最後にそれをlayerに上書きしています。各ノードの親子関係等の記入も、ここで行っています。また、layerのノード数が奇数だった場合、最後尾のノードの兄弟がいないので、自身の複製を兄弟として追加しています。

・build_tree

build_layerメソッドを、layerの長さが１になるまで繰り返すことでtreeを完成させます。その後、最上層のノードのハッシュ値をマークルルートとして格納します。

・search

任意のdataを持つノードをleavesから探します。

・get_pass

まず、任意のデータを持つノードをtargetとして保存します。targetの親を辿っていくことで、マークルパスを作成します。具体的には、親ノードの兄弟のhashとpositionが、マークルパスとなります。

もう一度図を見てみましょう。

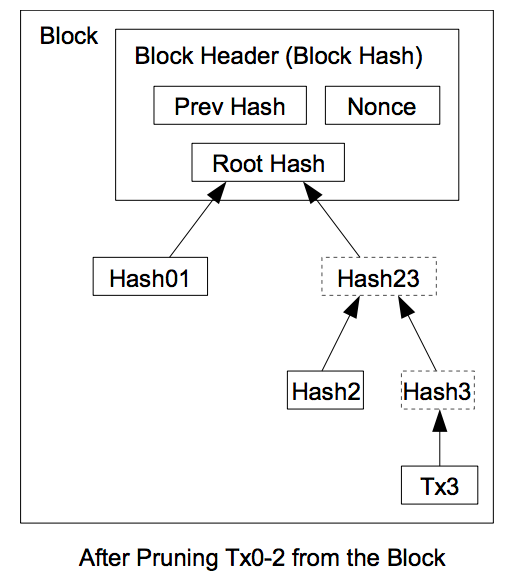
hash3とhash２があれば親（hash23）のハッシュは計算できるので、親はマークルパスになりません。一方で、親の兄弟（hash01）は算出できないので、マークルパスに追加します。また、足し算の順番によってハッシュ値が変わるので、positionもマークルパスに必要となります。

●caluculator関数

マークルパスからマークルルートを算出する関数です。先頭の値は足し算の必要がないので、そのままvalueに代入しています。その後は、マークルパスに則って足し算した値のハッシュ値を、valueに上書きしていきます。全行程を終えた時のvalueが、算出されたマークルルートとなります。

●使ってみる

ブロックチェーンとウォレットを再現するのは難しいので、ここでは単純なデータ群を使って動作を確認してみます。マークルパスを使うことで、データ群の全てを知らずとも、改ざんの有無を検証できることを見てみましょう。

まず、データを入れたリストからマークルツリーを作成し、そのマークルルートを表示させています。ブロックチェーンで言えば、各文字列がトランザクション、リストがブロック、そしてマークルルートがウォレットに格納されるデータです。

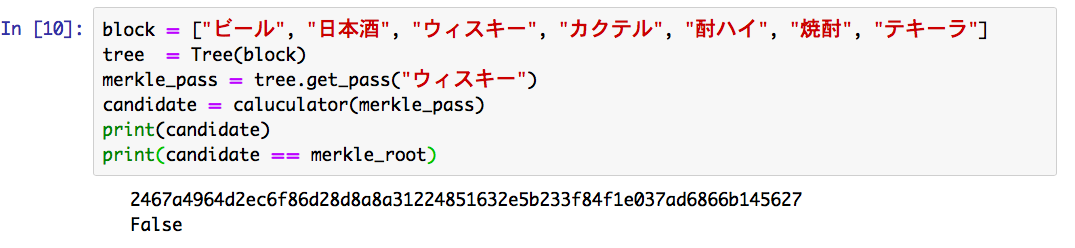
次に、ウィスキーから伸びるマークルパスを見てみましょう。0番目がウィスキーのハッシュ値で、その後はハッシュ値とpositionの組になってるのが分かります。

このマークルパスからマークルルートを算出し、先程取得したmerkle_rootと一致することを確認しましょう。

今度は、元データのノンアルをテキーラに改ざんしてみましょう。そこから先程と同様にして、マークルツリーからマークルパスを取得し、マークルルートを算出してみましょう。改ざん前のツリーのマークルルートと異なる事が確認できます。

●最後に

ちょいと難しい内容だっただけに、この記事だけで理解できないかもしれませんし、もしかしたら私の理解も何か間違ってるかもしれません。幸い、もずく先生も図解でマークルツリーを解説しようと試みているようなので、そちらと合わせて理解を深めていただければと思います。

読者の前提知識を一切考えず書いた俺得記事になってしまいましたが、いつか誰かの役に立てることを祈っています。

かしこ。