【ウェブで】開成中学入試２０１９年問題２解答解説【学ぼう】

図のような直方体ＡＢＣＤ-ＥＦＧＨがあります。

また、辺ＣＤ、 ＥＦ、 ＧＣ上にそれぞれ点Ｐ、 Ｑ、 Ｒがあり

ＤＰ=8cm、 ＰＣ=12cm、 ＥＱ=4cm、 ＣＲ=9cmが成り立っています。

３点Ｐ、 Ｑ、 Ｒを通る平面でこの直方体を切断し、切断したときにできる切り口の図形をＸとします。

図形Ｘを前から見ると(面ＡＢＦＥに垂直な方向から見ると)、面積が228平方センチメートルの図形に見えます。

図形Ｘを上から見ると(面ＡＢＣＤに垂直な方向から見ると)、面積が266平方センチメートルの図形に見えます。

このとき、次の問いに答えなさい。

(１)　図形Ｘは何角形ですか。

(２)　直方体の高さ(辺ＡＥの長さ)は何cmですか。

(３)　直方体の奥行き(辺ＡＤの長さ)は何cmですか。

(本番の解答用紙には、この下に計算のための余白があります。図形の作図も採点対象となります)

解答

(１)　六角形

(２)　14.4cm

(３)　20.3cm

解説

単元：中学受験算数　立体図形　切断図　平面図　立面図　平面図形　相似

受験生難易度：

１－（１）　易しい

１－（２）　易しい

１－（３）　標準

対策：立体図形の分野から、切断図の単元が出題されています。立体図形の切断図は、中学受験では頻出の単元ですが、ありきたりな図形を暗記するだけでは、対応できないでしょう。誰でも見知っているような図形は登場しません。

空間認知の訓練をして、どのような図形が登場してきても、自分の手で作図できるように準備しておきましょう。どうしても図形が苦手な場合は、他校の受験も検討した方が良い場合もあります。

受験生難易度は標準的で、図形が得意な生徒は、全問正解できる大問です。図形が苦手な生徒でも（２）までは正解したいです。立体図形の解法だけではなく、平面図形の解法も同時に求められていますので、記述はしっかりと筋道を立てて書きましょう。

分析：

（１）　六角形

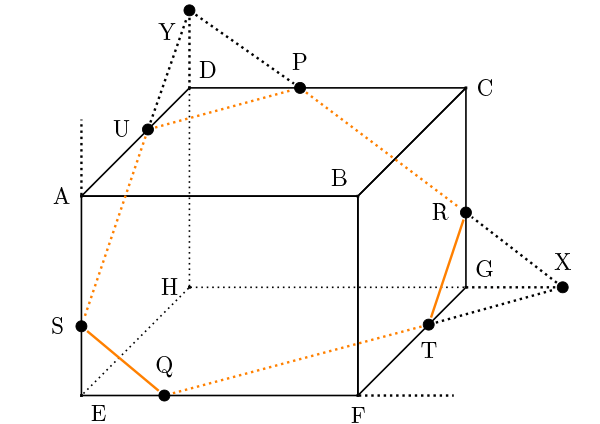
立体図形の切断　解法１：同じ平面の点を結ぶ

点Pと点Rは、同じ平面DCGHにあるので、線を引きます。

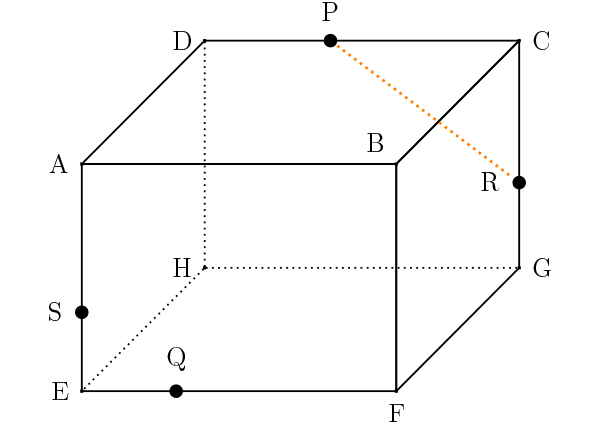
立体図形の切断　解法２：平行な面に平行な線を引く

平面DCGHと平面ABFEは平行な面なので、辺PRと平行な線を点Qから引きます。交点を点Sとします。

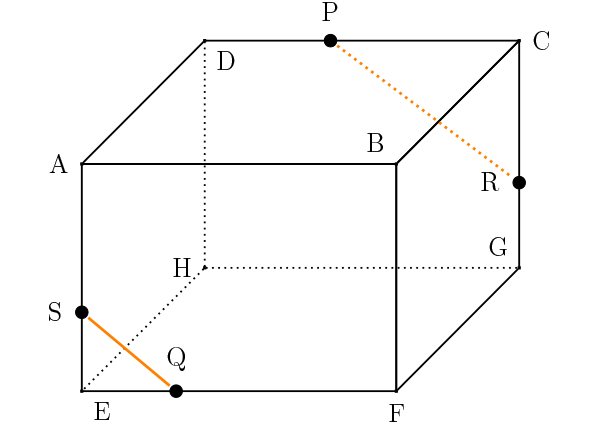
立体図形の切断　解法３：辺を延長する

辺PRを延長して、平面と交わるところまで補助線を引きます。

平面EFGHとの交点を点X、平面ADHEとの交点を点Yとします。

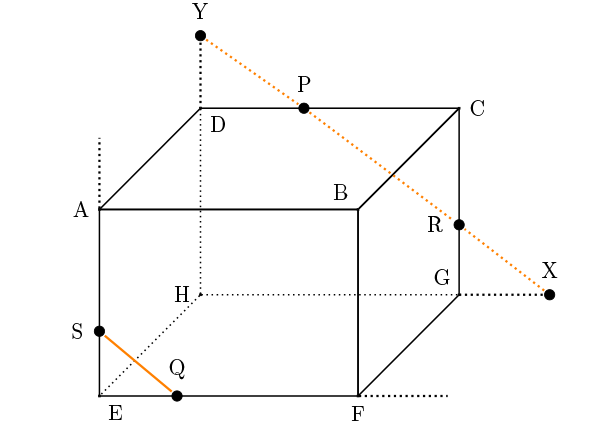
立体図形の切断　解法１の繰り返し：同じ平面の点を結ぶ

点Xと点Qは、同じ平面EFGHにあるので、線を引きます。辺FGとの交点を点Tとします。

点Yと点Sは、同じ平面ADHEにあるので、線を引きます。辺ADとの交点を点Uとします。

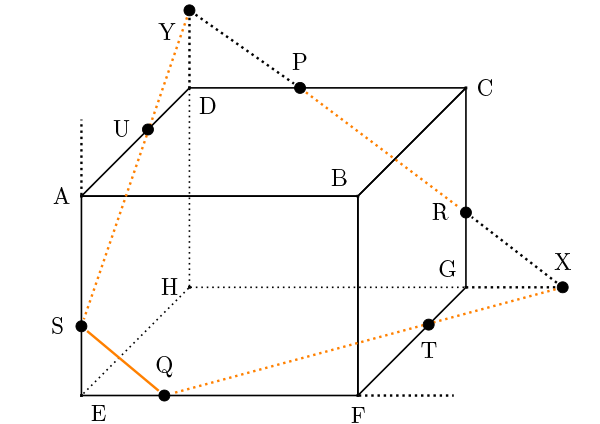
立体図形の切断　解法１の繰り返し：同じ平面の点を結ぶ

点Tと点Qは、同じ平面EFGHにあるので、線を引きます。

点Uと点Sは、同じ平面ADHEにあるので、線を引きます。

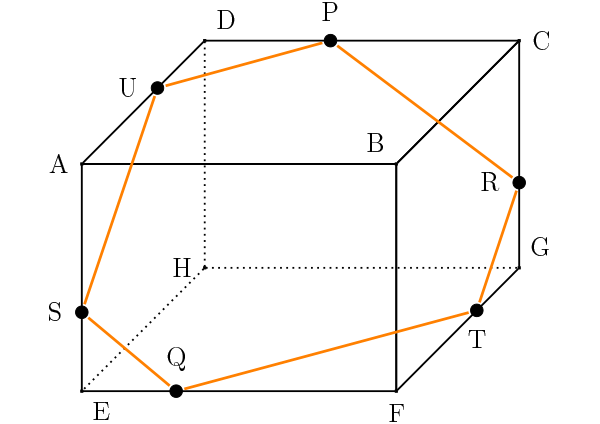
完成です。

答えは図形Xは六角形です。

立体図形の問題は、図形が描けなければ、そこで手が止まってしまいます。日頃から空間認知の能力を鍛えておきましょう。ちなみに、タブレットやスマホなどのデジタル学習よりも、手書きの紙でのアナログ学習の方が、より効果があることがわかっています。

【解説続き　原記事】