

こんにちは。ALIS CEO 安 (@YasuMasahiro)です。
前回のブログでは、「Radical Markets(革命的な市場)」の第一章に関してご紹介いたしました。今回は第二章のRadical Democracyについてご紹介いたします。基本的に第一章と第二章が本書の重要な部分としてよく語られておりますので、これらを抑えていればRadical Marketsに対する議論の土壌は整うかと思います。特に第二章は、Cryptoeconomics界隈においてはGovernanceの分野に踏み込んだ内容になっておりますので、こちらの章だけでも十分に参考になるというのが個人的な感想です。
では早速本題に入りましょう。
目次
第二章:革命的な民主主義
# Quadratic Votingとは
# 投票による政治の脆さ
# 民主主義の欠点
# 政治にマーケットの原理を持ち込む
# 発電所の汚染はどこまで許されるべきか?
# QVがもたらす利点
イベント告知:Radical Markets in Japan
---------------------------------------------------------------------------------------

第二章:革命的な民主主義
本章では、民主主義をアップデートする方法としてQuadratic Voting(本書に準ずる形で以下QVと称します)という手法が紹介されます。前提として、現状の民主主義(1人1票)では以下の2点の大きな問題を抱えているという問題意識を本章では設定しております。
1. 多数決の方式によりマイノリティがマジョリティによって容易に迫害されてしまう
2. 現状の投票制度では一票の重み付けがないことにより、美人投票などの様々な問題が発生している
なお、厳密には民主主義といっても様々な定義や切口が存在しますが、その整理や説明はQVの紹介に際してはいささか冗長であるため、上記の2点の前提を元に話を進めさせていただきます。
まず、その解決策となるQVとはどんなものなのかをご説明いたします。
Quadratic Votingとは
1. 一定量のCreditが全員に配布される。Creditは使わずに蓄積していくことも可能
2. そのCreditを消費して票を購入し、投票することができる
3. ただし、x票を購入する際に要するCreditはx^2である
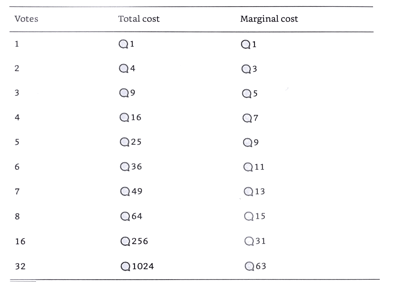
内容自体は非常にシンプルで理解しやすいかと思いますが、QVがなぜ民主主義をアップデートできるのでしょうか。現状の民主主義の問題を理解するためにも、少し歴史を振り返りながらQVの有用性についてご説明いたします。

投票による政治の脆さ
民主主義の起源は古代ギリシャにさかのぼります。当時の国力≒戦争力は、純粋に数が重要でした。その影響があってか、ギリシャの議会も社会的地位や所有財産に関係なく大勢の男性によって構成されていたそうです。この議会に所属する全メンバーが一票を持ち、法案を成立させたり、特権を与えたり、政治リーダーを処罰する等の議題を決めておりました。しかしながら、マジョリティで決めることの問題に古代ギリシャの議会は直面することになります。Peloponnesian WarのArginoussai Islandsでの戦いに勝利したのち、生存者を見殺しにして連れ帰ってこなかった将軍たちを死刑にするという判断を当時の議会は下しました。その原因は嵐によって将軍たちが動けなかったからだ、という説得によってなんとか死刑は免れましたが、マジョリティが下す判断の脆さを議会は痛感し、民主主義への疑念を募らせます。その後改良案として異なる階級で構成する混合組織を組成し、富裕層が一般層を利用したり、逆に一般層が富裕層を利用することをお互いに防ぐような方法も発明されました。この混合組織による方法は古代では最も長続きしましたが、お互いが案を否決しあうことであらゆることが徐々に停滞しはじめ破綻することになります。
その後、基本的に民主主義は長い間進化を止めることになります。ようやく現れた方法が三権分立によるcheck and balance(抑制と均衡)です。マジョリティによる統治を可能にしつつ、マイノリティの権利も担保するためにアメリカでも長年適用されている手法は、大統領制のもと議会を作り、最終的には大統領が判断するということでマジョリティの投票の力を制限し、なおかつ連邦裁判所が裁判等を通じてマイノリティの人種的・倫理的・宗教的な苦しみや迫害から守るというものでした。しかしながら、結局裁判官は民衆が選ぶことはできず一部のエリートから選ばれる以上彼らの価値観に準ずることになり、この方法も結局は不完全でマイノリティが迫害される事態は容易に発生しえます。
民主主義の欠点
加えて、18世紀に生きたフランス人のMarquis de Condrcetは以下のような民主主義の欠点にも気が付きます。それは、市民間で選好の衝突が発生したときに筋の通った結果を産み出す能力を欠いているということです。簡単な事例で紹介しましょう。
Antoine、Belle、Charlesの三人がいます。この三人に、ルイ14世への3つの処罰に関する選好を決めてもらいます。
・頭をギロチンで落とす
・王位に戻す
・一般市民として自由を与える
Antoineはギロチン>王位に戻す>自由を与える
Belleは王位に戻す>自由を与える>ギロチン
Charlesは自由を与える>ギロチン>王位に戻す
の選好を決めたとしましょう。
ここで彼らに3つの質問を投げかけるとそれぞれの回答は以下になります。
Q1. ルイ14世をギロチンにかけるか、王位に戻すか
A1. ギロチンにかける(Antoine, Charlesが選択)
Q2. ルイ14世を王位に戻すか、自由を与えるか
A2. 王位に戻す(Antoine, Belleが選択)
Q3. ルイ14世をギロチンにかけるか、自由を与えるか
A3. 自由を与える(Belle, Charlesが選択)
つまり、結果がひとつに定まることの無い奇妙な状況が発生します。ギロチンが王位に戻すことに勝ち、王位に戻すことが自由を与えることに勝ち、自由を与えることがギロチンに勝つ。
なぜこのようなことが起きうるのか。それは1票にその個人の選好の重み付けがされていないからです。ただある結果を他の結果より望むということしか反映することができず、どの程度その結果を望むのかが反映されていません。Kenneth Arrowは"impossibility theorem"としてこのような問題を解決できる投票制度はないことを示しました。

政治にマーケットの原理を持ち込む
一方で注目したいのは、市場の取引は商品やサービスへの嗜好を価格という形で反映することができます。多くの経済学者が市場は効率的な結果をもたらし、投票では実現不可能であることを信じるゆえんでもあります。つまり、市場の原理を民主主義にも適用することで、より良い形で資源を配分することができる、それもより強いニーズや関心をもつ人たちに対して、ということが述べられています。
しかしながら、どうやって政治に市場の原理を持ち込むんだ?という当然の疑問が産まれると思います。一般的に政治はきれいな空気や防衛力や公衆衛生などの"公共財"を作り出すためのもので、現在のマーケットで取引されている私財とは全く異なる性質のものです。政治に対して、市場と同じように最も高い値段をつけた者に決定権を与えるとなると、恐ろしい結果を産んでしまうことは想像に難くないでしょう。ここでひとひねりします。
最も高い値段をつけた人に決定権を委ねるのではなく、その決定による行動が他者に課すコストのトータルを、決定権を下したそれぞれの個人が分担して支払う形にすれば良い
また、この個人が公共財に影響を及ぼすために支払うコストは、個人がもつ影響の割合ではなく、その二乗(quadratic)に基づく必要があるとも述べられています。
こちらも例を挙げて説明いたします。

発電所の汚染はどこまで許されるべきか?
ある発電所が存在しており、低コストで電力を供給する一方で汚染も引き起こしてしまうとします。電力の恩恵は人々がお金を支払って使用しているという意味でわかりやすいですが、汚染の影響に関しては不透明です。政府は規制を用いて汚染の影響を抑制するよう発電所に要望しますが、その分のコストが料金に反映され電気料金は上がります。
話をシンプルにするために環境汚染に関する倫理的な観点は一度無視した時の疑問は、一体どれぐらいの人が汚染を気にするのか?ということです。それを明らかにするために、今一般的に行われる方法として多数決による投票を使い、耐えうる汚染のレベルについて人々に決めてもらうとします。しかしながら、喘息持ちなどの身体の弱い方や、ご高齢の方々が気にする汚染のレベルはマジョリティの気にするレベルよりも高いはずですが、多数決による投票ではどちらを重視すべきかについて答えることができません。これを解決するためには、問題への関心の深さ、つまりマイノリティの問題への関心度の高さとマジョリティの問題への関心度の低さを比較する必要があります。
そこで投票の代わりにある実験を行うとしましょう。それぞれの市民に追加の汚染を避けるためにいくらのコストを支払いたいと思うか?ということを質問します。一方で、最大多数の最大幸福という視点に経った場合、汚染を許容することで得られる価値は電力の販売による便益です(本書に合わせる形でただ便益と書いていますが、その効用や税収などを含む公共の利益を意味します)。便益を最大化するための最善の策を決めるには、この市民が支払いたいと思うコストと電力の販売による便益が相殺されるポイントまで汚染を許す(電力を発電する)ことです。
以下の図は、これらの汚染と電力の価値を図にしたものです。あくまでも単純なモデル化をしていることにご留意ください。
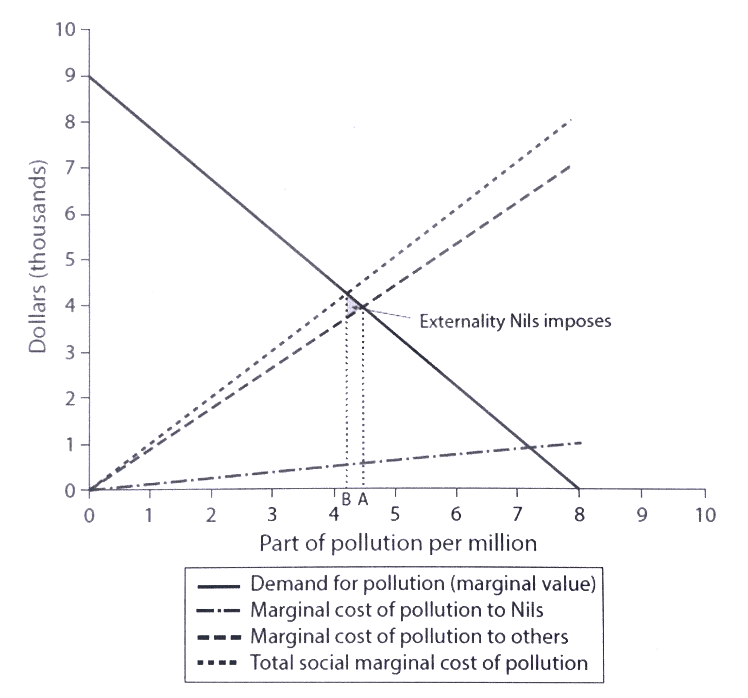
右肩下がりの線は発電による経済価値を表しています。一定量の汚染を行う場合の発電所の発電能力に限界があることと、そもそもの電力需要を鑑みると、発電量が増えれば増えるほど(=汚染が発生すればするほど、汚染対策のコストが上昇すれば上昇するほど)経済価値は下がってしまう、右肩下がりの線になることは想像に容易いと思います。
一方で、右肩上がりの点線のうち最も傾きがゆるいものがNilsというある市民(1人の個人です)が支払うコストの線です。彼はランドリーを経営しているので、汚染により洗濯物の汚れを落とすのがより難しくなり、彼は汚染が進むほど余分なコストを支払うことになります。
次に傾きのゆるい線がNils以外の市民が支払うコスト(この場合はNils以外の市民全員分の合計のコストを表します)で、最も傾きが急な線がNilsを含めた全市民が支払うコスト(前の2本のラインの合計)です。つまり、Nilsがこの街に住んでいることにより、利益とコストが相殺する点がAからBに移ることになります。
この時Nilsが汚染を避けるために支払うべきコストはいくらになるのでしょうか。答えは、彼が汚染を減らすために他の市民に課すことになったコストです。なぜならば、Nilsが汚染によって損害を受けるランドリーを持っているがゆえに電気料金があげられなければならないとすると、従来の低い電気料金で得られていた市の純便益(便益-費用)を減らすことになるからです。彼の負担するコストは、上記のグラフの灰色の三角形の部分になり、その面積はAとBの距離の二乗に比例します。
少し長くなりましたが、こちらが
個人が公共財に影響を及ぼすために支払うコストは、個人がもつ影響の割合ではなく、その二乗(quadratic)に基づく必要がある
と先述した根拠になります。

QVがもたらす利点
大分前置きが長くなってしまいましたが、ようやくQVの利点について説明する土壌が整いました。冒頭で申し上げた通り、QV自体の仕組みはシンプルです。
1. 一定量のCreditが全員に配布される。Creditは使わずに蓄積していくことも可能
2. そのCreditを消費して票を購入し、投票することができる
3. ただし、x票を購入する際に要するCreditはx^2である
※なぜ一票の購入にその二乗のコストが必要であるかは、先程の発電所の例で明らかです。

Yes, No, 無関心のいずれかの選択肢しか無かった現在の一人一票の制度とQVが決定的に異なるのは、志向の強さを反映することができる点です。Creditを蓄積できること、および一つのテーマに一票以上投じることができるためです。これにより、マイノリティがマジョリティを投票で制する余地が産まれ、最大多数の最大幸福を満たすことはできないが、限りなく近いことはQVによって実現できるだろうと述べられています。
また、政治にマーケットの原理を導入する場合、あるテーマに対して関心の高い人はいくらでもお金を出して票を買い集めてしまう事態が発生しますが、ある票を購入するためにその二乗のCreditを要求するというQVはこの問題も解決できます。フリーライダー問題も解決することができる手法としても言及されており、こちらのブログ等が参考になるかと思いますのでお時間があればご一読ください。
加えて上記図のMarginal cost(次の票を購入するために追加で支払うべきコスト)を見ていただきたのですが、3票を持っている人が4票目を購入したい時のMarginal costは7、7票持っている人が8票目を購入したい時のMarginal costは15と、約2倍の関心を持ち票を購入したい人は約2倍のMarginal costを支払わなければならないと言う点も絶妙に設計されている点です。
ただしQVが役割をなすのは個人が合理的で理性的な場合に限ります。これは一人一票の問題でも起きることではありますが、談合や投票の買い占めや不正などが起これば当然QVは役割を果たすことができません。通常このような問題に対しては法律や社会規範で厳しく制限されてはいますが。
ただ、それ以上に根本的な疑問が持ち上がります。「最大多数の最大幸福なんてどうやって達成するのか?」と。ある個人の幸せが他の個人の幸せに比べることは可能なのか?と。多くの経済学者はこの質問はナンセンスで、我々が望むべきは「他者の幸福を減らすことなくほかの誰かの幸福を上げることができる」、いわゆるパレート最適な状態を目指すべきであるし、全体の幸福が公平に分配されていることを望むべきだと考えています。QVによって、マジョリティが強い関心を持つテーマに関してマイノリティが変えることはできないかもしれませんが、マジョリティの興味が薄いテーマに関してはマイノリティがQVを利用することで、全体の福祉は現在よりも改善される可能性があります。
---------------------------------------------------------------------------------------
本はこのあとも少し続き、QVを擬似的に政治に適用するという実験の結果や、GAFAやシェアリングエコノミーサービスの中核である評価システムにおいてもQVは利用できるのでは(実際の利用例は本書では提示されておりませんが)などの考察の紹介がありますので、気になる方は本書を手にとってみてください。
QVの概念自体は非常に分かりやすく導入難易度も高くはないので、ALISでもどこかで導入してみたいと考えています。例えばトークン保有量に応じてCreditが配布され、QVによって開発案件やプロジェクトの方向性を決めるなど。それによって全体の利益・福祉が最大化されることが実現できれば良いですが、本書でも述べられている通りそれを計測することが難しいのが課題かなと思います。
他にも、Creditをためておくことができるという性質により、談合や票の買収による不正が従来の仕組みより起きやすくなる点や、Creditの付与の設計をどうするかなど細かい点で気になる事はたくさんありますが、従来の仕組みよりも選好が反映されるという点は大きなメリットに感じるので、積極的にユースケースをためてシェアしていきたいですね。
--------------------------------------------------------------------------------------

イベント告知:Radical Markets in Japan
さて、第一章・第二章とRadical Marketsについてご紹介いたしましたが、5月7日(火)に渋谷のNeutrinoにてイベントを開催いたします!
先日公開した第一章の要約記事が著者のGlenの目にとまりまして、Radical Marketsの日本ブランチを立ち上げようという話になりました。僭越ながらグローバルと日本のRadical Marketsの架け橋となるべく尽力いたします。私自身がDetroitで参加したRadicalxChangeのイベントのレポートなども当日はお伝え出来ればと思います。
Radical Marketsに関心のある方々にお集まりいただき、理解を深めながら議論を行えるような場に出来ればと思いますのでEconomy, Governanceの分野にご興味のある方は是非お集まりください!
イベントの詳細は以下のページをご覧ください。ご参加お待ちしております!
https://radicalmarkets-japan.peatix.com/
---------------------------------------------------------------------------------------

書いた人:ALIS CEO 安 (@YasuMasahiro)
*Radical DemocracyやQVに関する情報はTwitterでも発信しています。ご興味あればフォローをお願いします!
・間違いの指摘や反論など大歓迎です
・この記事は、運営による記事のためいいねによるトークン配布はありません
・ALISではエンジニア・R&Dメンバー絶賛募集中です 😉

コインチェックに上場が決まったEnjin Coin(エンジンコイン)コインを解説
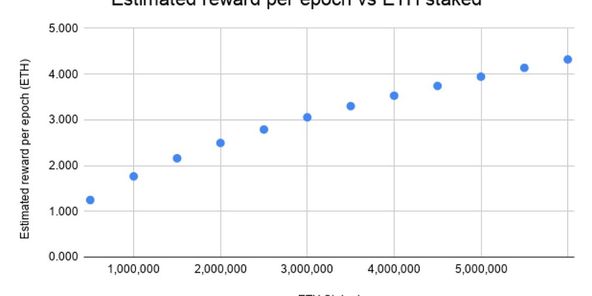
Eth2.0のステークによるDeFiへの影響を考える。
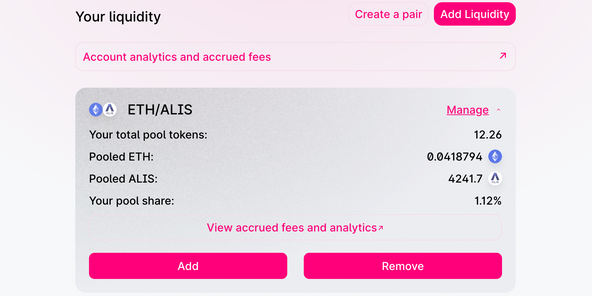
Uniswap(ユニスワップ)で$ALISのイールドファーミング(流動性提供)してみた

2021年1月以降バイナンスに上場した銘柄を140文字以内でざっくりレビュー(Twitter向け情報まとめ)

17万円のPCでTwitterやってるのはもったいないのでETHマイニングを始めた話

【第8回】あの仮想通貨はいま「テレグラム-TON/Gram」

Uniswap v3を完全に理解した

CoinList(コインリスト)の登録方法

約2年間ブロックチェ-ンゲームをして

バイナンスの信用取引(マージン取引)を徹底解説~アカウントの開設方法から証拠金計算例まで~

【DeFi】複利でトークンを運用してくれるサイト
