NIST PQC 標準化プロセスに関連した知識の体系化①（【いま、ブロックチェーンが危ない：⑥】）

METEORA SYSTEM Co., Ltd. は,渡邊の[非可換algorithmによるBlockchain耐量子化技術] について, License partner の募集を開始しました. Cryptography の歴史を変えてくださる方との出会いを心待ちにするとともに, 候補者の方との積極的な discussion を歓迎しております.

ブロックチェーンの 量子耐性化 を実現する渡邊の 非可換アルゴリズム について、その独特なはたらきを紹介しました。

ここからは、この 非可換アルゴリズム への理解の一助とすべく、永らく信奉されてきた 可換アルゴリズム との関係を2編にわたって整理し、知識の体系化を試みます。

1976年に戻って未来へ

Abstract

1976年、 Diffie-Hellman-Markle は鍵配送のジレンマを解決しました。

それ以前に鍵配送の現実的なシナリオはあるにはありましたが、そのシナリオは「DES に二重に鍵をかけたら、逆順に鍵を外さねばならない」という逆順のルールに邪魔され情報技術として実現しませんでした。

しかし、Diffie-Hellman- Markle は DES の逆順のルールに縛られませんでした。この数学は可換アルゴリズムです。そして RSA も可換アルゴリズムであることが容易に判ります。可換アルゴリズムは逆順のルールに邪魔されない、これは画期的な発明でした。が、Shannon の数学は量子耐性を保証しません。このシステム を量子耐性にしたいなら鍵生成が「うそ」をつかねばならないからです。

2014~18 年筆者(渡邊)は、逆順のルール に潜んでいる AES の Shannon エントロピーから、一方向関数を創ることに成功しました(実装もしました)。これが 非可換アルゴリズムの誕生です。

非可換アルゴリズムは可換ではないため 公開鍵に互換ではない 、しかしその安全性は現実の習慣に寄り添う。

NIST の Post-quantum cryptosystem(PQC)は可換アルゴリズムに属するもので決着するでしょう。本稿では非可換アルゴリズムの光に照らして見たところの PQC の着地点 を議論します。

本論はここから 1976 年にさかのぼります。

1. 可換アルゴリズム

1.1 Diffie-Hellman-Markle

Fig,1 は D-H プロトコルが可換アルゴリズムであることを示そうとしています。Yα(mod P)という形式 の一方向関数が活躍します。αは内部変数です。

アリスは α1 を手元に置き、ボブは α2 を手元に置き、外部変数 Y と P の値をアリスとボブが取り決めます。取り決めに際し、大声を出しても問題はありません。 

第三者から見ると α1 と α2 は確率変数であるので、計算 Yα1 (mod P) と Yα2 (mod P) を関数の形で 下記のように表現します。

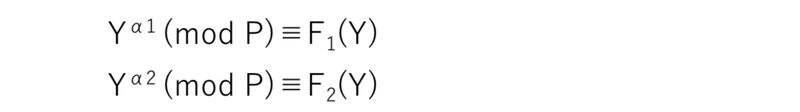
Fig.1 の S2 と S1 は各々次のように関数形で与えられます。

結局、Diffie-Hellman-Markle 鍵配送は次のように要約されます。

ここで F2(F1(Y))と F1(F2(Y)は Y に関する各々多重暗号である。多重暗号の差分(S1 - S2)をエントロ ピー常数と定義する。

(S1 - S2)≡エントロピー常数-----------(2)

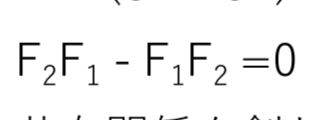
なる式が可換アルゴリズムです。可換アルゴリズムがあれば、アリスとボブは秘密の共有関係を創れます。これには認証機能が欠落していて、秘密の共有関係を任意の二人に保証するのは難しい。

エントロピー常数ゼロは二者間に Shannon エントロピーの壁が無いことを意味します。エン トロピーの壁が無いことは当然、秘密の共有関係を危機に陥れる原因となります。

1.2 RSA

1975 年の夏、Diffie は非対称鍵の構想を発表しました。リヴエストの思考回路はそこに止まります。「Diffie の言う非対称鍵は実際に有るのだろうか?」と。今、受信者アリスが持つ特別の情報(鍵)を K1 と表し、送信者ボブが持つ鍵を K2 と表します。

鍵配送の現実的なシナリオでは、ボブが最初に、乱数 x1 を振り出し、これに K2 で鍵かけをしてから暗号をアリスに送ります。さらに受信者アリスがその暗号に K1 で鍵をかけて下記の(3)をボブに返送します。二重に鍵の掛かった暗号を確率変数 P で表すと、

P2=K1(K2(x1)) -----------(3)

これは確率変数 P で二重に鍵の掛かった暗号を表します。ここから鍵配送のシナリオは鍵を外すプロトコルに入ります。

もし、DES なら「逆順に鍵を外さねばならない」というルールに邪魔されてボブは(3) の鍵 K2 を外せません。

もう一つのやり方は、アリスが送信者になり、乱数 x1 を振り出し、これに鍵 K1 を掛けてボブに送る場合です。今度は受信者ボブが鍵 K2 を掛けてアリスに返送します。

そうするとアリスもまた「逆順に鍵を外さねばならない」ルールに邪魔されて(4)の鍵 K1 を外せません。

P1=K2(K1(x1)) -----------(4)

ここでもアリスは鍵 K1 を(4)から外せません。このように逆順のルールに邪魔されて(3)/(4)を復号する アルゴリズム が無いわけです。

リヴエストはなお考えました。「受信者が特別な情報を持っている時に限り、一方向関数の逆向き計算が可能になる、そのようなアルゴリズムが見つかるだろうか?」と。これが見つかった時、「受信者アリスはボブに P2 を返送する必要が無い」。なぜなら、特別な情報としての鍵 K1 を掛けた時点で、 アリスはボブの乱数 x1 を手に入れるからです。次の通りです。

2=K1(K2(x1)) =x1-----------(5)

ボブも特別な情報としての鍵 K2 を掛けた時点で P1 を返送する必要が無く、アリスの乱数 x1 を手に入れることができます。

P1=K2(K1(x1)) =x1-----------(6)

上記の通りであれば、D-H プロトコルと同じ成り行きになります。

P1 - P2 = K2(K1(x1)) - K2(K1(x1)) = x1 – x1 = 0-----------(7)

ここでもエントロピー常数はゼロになり、関数 K1() と K2 () は可換になります。アリスとボブは秘密を共有する関係を創ることができます。

しかし、アリスとボブの間に Shannon エントロピーの壁はなく、壁の欠落はシステムを危機に陥れる原因になります。

このように可換アルゴリズムは鍵を公開する技術ではなく、鍵を配送する技術です。それゆえPost-quantum cryptosystem(PQC)が公開鍵に互換であろうとするなら、PQC は当然、可換アルゴリズムのルールに従うことになる。

そうすると、鍵 k1 と k2 のどちらかをネットに公開するためには鍵生成は「ウソ」をつかねばなりません。

2. 鍵生成は「ウソ」をつかねばならない

PQC が公開鍵と互換である限り、いかなる数学技巧が駆使されようとも、PQC は下記 Shannon entropy の数学に拘束されます。ここで H() は Shannon エントロピーを計算します。

今、鍵 K1 から K2 への計算は容易だといいます:→hH(K2|K1)=0。

他方、鍵 K2 から K1 への計算は複雑でプログラムの開発が難しいといいます。

難しいといっても、計算困難性の Shannon エントロピー もまた H(K1|K2)=0 です。

この計算困難性を H(K1|K2)>0 のごとくいうとしたら、それは「ウソ」 です。

もっと詳細に「ウソ」を見てみましょう。

鍵 K2 と K1 の同時確率エントロピーには、二通りの表現があります。

H(K1, K2)=H(K1) + H(K2|K1) ---------(12-1)

=H(K2) + H(K1|K2) ---------(12-2)

最初の鍵 K1 から K2 の計算は容易だというのは (12-1) にて H(K2|K1)=0 になります。それで (12-1) は (13) になります。

H(K1, K2)= H(K1) ---------(13)

もう一つは (12-2) 、鍵 K2 から K1 への計算は複雑だと言うが、H(K1|K2)≠0 にはなりません。なぜならその計算に不確定はないから H(K1|K2)=0 になります。

ここで筆者(渡邊)は「ウソ」をつきます。

鍵 K2 を公開し→H(K2)=0、鍵 K2 を条件とする K1 の Shannon エントロピー H(K1|K2) はゼロにならない、という「ウソ」です。

H(K1, K2) = H(K2) + H(K1|K2) = H(K1|K2)≠0 ---------(14)

これが正しくないことは、(13)と(14)から(15)式が出てくることから判ります。

H(K1)= H(K1|K2) ---------(15)

これは鍵 K2 と K1 は独立であるという式です。

先に鍵 K1 から K2 への計算は容易だと定義したから、(14)式は「ウソ」をついていることが判ります。ただ、下記の不等式に「ウソ」が隠れる場合があります。

H(K1)> H(K1|K2)>0 ---------(16)

長い時間なら H(K1|K2)=0 になり、短い時間なら H(K1|K2)>0 です。

(16)式が「ウソ」をついている事実を積極的に隠している訳ではなく、「ウソ」が隠れるように標準化プロセスが知恵を出す努力を認める、そういう不等式です。

実際、PQC-forum はそういう議論をしているし、標準化プロセスは最適化の議論を歓迎しています。

この不等式から学ぶことがもう一つあります。

候補者が実装環境のサポートを求めていたら、それを 欠点と見るのではなく、「ウソ」を隠す環境を求めていると考えてみることです。

また、候補者はいずれも長所と欠点を帯びているように見えるけれど、それは客観的な事実ではなく、不等式(16)の中だけに存在する PQC に過大な期待をしているからである、と考えてみてはどうでしょうか。

私がこのように述べる背景には非可換アルゴリズムがあるからです。

(次回記事へ続く・・・。)

©︎2021 METEORA SYSTEM Co., Ltd and Kosaka advisory office