NIST PQC 標準化プロセスに関連した知識の体系化②（【いま、ブロックチェーンが危ない：⑦】）

前回の記事では、従来の方式である可換アルゴリズムの性質やモデルについて整理しました。

ここからはメインテーマである非可換アルゴリズムについてみていきます。

METEORA SYSTEM Co., Ltd. は,渡邊の[非可換algorithmによるBlockchain耐量子化技術] について, License partner の募集を開始しました. Cryptography の歴史を変えてくださる方との出会いを心待ちにするとともに, 候補者の方との積極的な discussion を歓迎しております.

3. 非可換アルゴリズム

非可換アルゴリズムは現実的な鍵配送シナリオ(前回記事Fig,1)を DES 又は AES で表現したプロトコルと して定義することができます。このプロトコルは逆順のルールに従うことを我々に強制します。

ここから脱出に成功した者が D-H プロトコル と RSA であり、歴史はそのように教えています。再び、先の(3)と (4)をここに掲載します。

P2=K1(K2(x1)) -----------(3)

P1=K2(K1(x1)) -----------(4)

ボブは逆順のルールに当面し、(3)の鍵 K2 を外せません(K1 はアリスが持っている)。

アリスも逆順のルールに当面し、(4)の鍵 K1 を外せません(K2 はボブが持っている)。

ボブにとってもアリスにとっても第三者にとっても、暗号 P を復号する鍵が手に入りません。したがって、(3)と(4)の差分 {P1- P2} はゼロにならず、圧倒的な確率で次式を満足します。

{P1 - P2}≠0 ---------(17)

ここではゼロエントロピー常数は現れません。したがって、関数 K1()と K2 ()は非可換。

これの売りは アリスとボブの間に Shannon エントロピーの壁が在ることです。この壁が在るゆえにシステムが危機に陥ることを防ぎ、また、この不等式(17)から一方向関数が立ち上がります。説明します。

3.1 リヴエストの思考回路は受信者を出発点に置く...しかし

リヴエストの思考回路は...受信者が特別な情報を持っている時に限り...とあるように、受信者が出発点です。 しかし、ここでは送信者アリスが出発点です。

送信者アリスは、(3)/(4)の鍵 K1 と K2 をランダムに選び(鍵生成を行い)、任意の文書のハッシュ値 x1 からコード P1 と P2 を作る、又は、複数のノードから来た乱数の合計を入力に持つハッシュ値 x1 からコード P1 と P2 を作ります。

P1= K2(K1(x1)) ---------(18-1) P2= K1(K2(x1)) ---------(18-2)

この作り方は次の通りです。

アリスはデータ x1 を AES1 のノードに移動し K1(x1) を出力し、次に K1(x1) を AES2 のノードに移動し P1 を出力します。P2 についても同じ、ただ移動の順序が異なります。要するに、 K1(x1) と K2(x1) が仮想ネットワークの中を移動してコード P を出力する訳です。

コードを P1 と P2 の二つだけにする理由は特になく、n 個用意できます。(18) 式はたまたま2個です。

(18) 式を関数の形式に表します。AES 鍵空間の一点を Y1、他の一点を Y2 と定義する。そうすると、鍵 Y1 を掛ける変換 が Y1() で表され、鍵 Y2 を掛ける変換が Y2()で表されます。以下の通りになります。

P1=Y1(x1) ---------(19-1) P2=Y2(x1) ---------(19-2)

特筆すべきことは、アリスが生成した鍵 K1 と K2 はデータとして存在するが、鍵 Y のデータはどこにも無い、つまり Y は AES 鍵空間に確かに存在するが、データとしては取り出せないことです。

3.2 関数 Y1()と Y2()各々は一方向関数ではない

式(19) の変換ペア {Y1(), Y2()} はハッシュ値 x1 をコードペア <P1, P2> に変換します。変換ペア {Y1(), Y2()} は鍵 Y をセットされた暗号関数と見えます。その復号鍵が無いから、新しい一方向関数かも知れないと期待します。

しかし、Y1() と Y2() 各々は一方向関数に成らない:コード Y(x1) から x1 を取り出す方法が有る:それが逆順のルートです。

(19-1):Y1(x1) が AES2 から AES1 へ移動すれば x1 が姿を現し、(19-2):Y2 (x1) が AES1 から AES2 へ移動すれば x1 が姿を現す。

それで Y1() のバックドアを Y1-1() と表し、Y2() のバックドアを Y2-1() と表すと、下記のようになります。

x1= Y1-1(P1) ---------(20-1) x1= Y2-1(P2) ---------(20-2)

バックドア (20) が有るので、逆向き計算が可能になります。

3.3 バックドアを塞ぐための「確率計算式」

コード P1 と P2 が「同期」して (20) に入ると、各々のバックドアが塞がれるコード P1 と P2 の同期入力を <P1, P2> と表す。すると、コードペア <P1, P2> は x1 で「衝突」します。

その他の任意のコード を {P1, P2} と表記すると、{P1, P2}は衝突しません。下記 Fig.2 は正確な図解です。

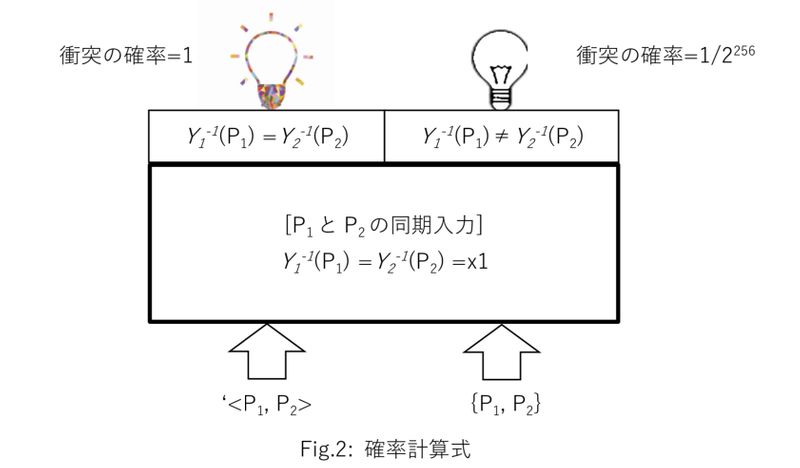
図中、左側が <P1, P2> の衝突、右側が {P1, P2} の衝突です。衝突を検査する式が下記 (21) です。

Y1-1(P1) =Y2-1(P2) =x1 ---------(21)

(21) に記入されたイコールはイコールにするペア <P1, P2> を求める代数式ではなく、x1 に衝突するか否かを検査せよ、というプログラム要件です。

このように、衝突が確率 =1 のイベントと確率 =1/2^256 のイベントに分かれるので、(21) を確率計算式といいます。確率 =1/2^256 のイベントを起こす任意コード {P1, P2} についてはハッシュ関数への第二原像攻撃と同じ動作になる:第二原像攻撃の場合は、 Birthday bound(2n/2 回の探索) で x1 に衝突します。

3.4 関数ペア {Y1(), Y2()} が一方向関数である、なぜなら

任意コード {P1, P2} は確率 =1/2^256 の衝突を起こすが、コードペア <P1, P2> は確率 =1 で衝突を起こします。コードペア <P1, P2> を運用するアリスは確率 =1 で x1 を手に入れるが、その他の人は入手できません。

したがって、アリス以外の人にとって、関数ペア {Y1(), Y2()} は一方向関数であるす。これを 「知識分割」 といいます。このように 「知識分割」 は送信者アリスが行います。知識分割は 「全単射かつ一方向」 の関数アンサンブル <Y1(), Y2()...Yn()> です。

確率計算式については、天国へ通じる 「針の孔」 に喩えることができます。

1)所定のルールを守って来た者には、針の孔はたった 1 回の計算で「針の孔」を通過する。

2)所定のルールを守らなかった者には、針の孔は 2^256 回の労働を課す。

この 2^256 回の労働は量子計算機にも課せられます。なぜなら、量子計算機は「知識分割」に関与していないからです。

ここで特筆すべきことが有ります。

知識分割は一方向の暗号関数である一方、確率計算式にはコードペア <P1, P2> を x1 に復号する機能と認証する機能があります。つまり、復号機能は認証機能を伴い、復号と認証が一体である、知識分割はそういう内容を持っている点です。

さらに、認証にも特筆すべきことがあります。 第三者の証明書に代わり、コード P1 と P2 が互いに他を認証する。それ故、PKI のような 第三者基盤 が要らない点です。

3.5 公開鍵互換の PQC を見る準備

非可換アルゴリズム はまず、

◆量子コンピュータに 2^256 個の任意コード{P1, P2}を与える:言い換えると 2^256 回の労働を課す。

次に、

◆知識分割は実装環境を選ばない。

三番目に、

◆それ自体は鍵配送を行えない。

四番目に、

◆確率計算式が与えられ、複数のコード<P1, P2...Pn>が互いに他を認証する。

五番目に、

◆知識分割の利用は従来のアプリケーションと互換ではない。従来のアプリケーションのセキュリ テイ・ホールを埋めて余りある。

たとえば、

1) <P1, P2> をパスワードとして運用する:「非対称パスワード」。パスワードの理想を追い求める人がいれば、彼は非対称パスワードに 100% 満足するでしょう。

2) <P1, P2> と確率計算式でハッシュ値 x1 を再現し(衝突)。これで文書の改ざんを検証する:その際、検証者は署名が唯一であることを検証します。

3)知識分割サービスを二人以上、何人にも行える。社内データベースへのアクセス制御に最適でしょう。

4. 上記、知識の体系から見た PQC

以上のように、本稿は互換のアルゴリズムと鍵生成、そして前者の対極の非互換のアルゴリズムを論じてきましたが、筆者(渡邊)が立てた仮説は何もありません。

1976年に戻り、鍵配送の現実的なシナリオを公理にし、首尾一貫して公理から定理を論じてきただけです。それで、互換と非互換はワンセットであることが判ります。ちょうど、プラスが有ればマイナスも有るように。

先に、公開鍵互換である限り、PQC は鍵生成が「ウソ」をつかねばならないことを述べました。「ウソ」を許容するのはこの不等式 (16) です。ここには PQC 標準を一つに絞る数学的な基準はなく、複数になる方が理屈に叶います。賛否両論や、欠点と長所を裁定する情報理論の支援がないため、それで非可換アルゴリズムから手がかりを得たいと思いました。

上記 3.5 から公開鍵互換 PQC を眺めると、PQC に期待したいことが出てきます。非可換アルゴリズムには出来ないことがあり、それは鍵交換です。特に、公衆網における鍵交換は可換アルゴリズムにしかできません。

これについてはマニアックに考える必要はありません。

ここから先は筆者(渡邊)の主観が入りますが、たとえば、Forward secrecy まで考えた鍵交換プロトコルを考えると、このためには公開鍵は長い時間 「ウソ」 をつかなければなりません。利便性を犠牲にしてでも、公開鍵(PQC)が長い「ウソ」をつくことの方が重要です。

もっと言えば、PQC の適用分野を広げる必要はありません。IoT のためには軽い PQC が必要だと仮定してみると、このような考え方が邪魔をして絞り込みが上手く行かなくなります。

というのは、筆者(渡邊)は IoT のための優れたプロトコルを知っており、それはもちろん量子耐性、かつ公開鍵と独立なプロトコルです。

以上、PQC の絞り込みの参考になれば幸いです。

May 30, 2019

EIJI WATANABE

※本稿は、開発者渡邊(弊社代表)が2019年に NIST へ提供した記事の日本語訳です