【ウェブで】開成中学入試２０１９年問題３解答解説【学ぼう】

空間内または平面上にひかれた道を進んで、点Aから点Bまで移動するとき、その移動経路が何通りあるかを考えます。 


（１） 

《図１》は一辺の長さが１の立方体を４個組み合わせて、横幅(よこはば)２、高さ２、奥行(おくゆき)１の直方体をつくり、その直方体と点Aと点Bを結ぶ道をつけたものです。

図の中で点Aと点Bを結ぶ太線が、通ることのできる道です。 

《図２》は一辺の長さが１の立方体を４個組み合わせて、横幅(よこはば)４、高さ１、奥行(おくゆき)１の直方体をつくり、その直方体と点Aと点Bを結ぶ道をつけたものです。
《図１》と同じく太線で表された道を通ることができます。 

これらの道を、右、上または奥のいずれかの方向に進むことで、点Aから点Bまで移動するとき、考えられる移動経路は、《図1》、《図2》のそれぞれについて何通りありますか。

解答

(１)　
《図１》　１０通り
《図２》　１８通り

解説

単元：中学受験算数　道順　立体図形　平面図形

対策：平面図形の分野から、道順の単元が出題されています。道順は、標準的な解法では、ただ数えていくだけです。注意深い受験生であれば、正答できます。

しかし開成中学では、図形を平面から立体に置きかえたり、途中で道順を戻れるように条件設定をしています。解法を丸暗記するのではなく、条件設定が変えられた場合でも、対応できる思考力が求められています。いいかえれば、自分の頭で考えられる受験生を求めています。

分析：
（１）は空間図形の問題に見えますが、平面図形に直して考えると、簡単です。

【道順　解法：交差点に本数を書いていく】

《図１》の立体図形は、右移動と奥移動は、平面図形の場合と同じように考えることができます。平面図形の場合と同じように、交差点に道順の本数を書いていきます。
 

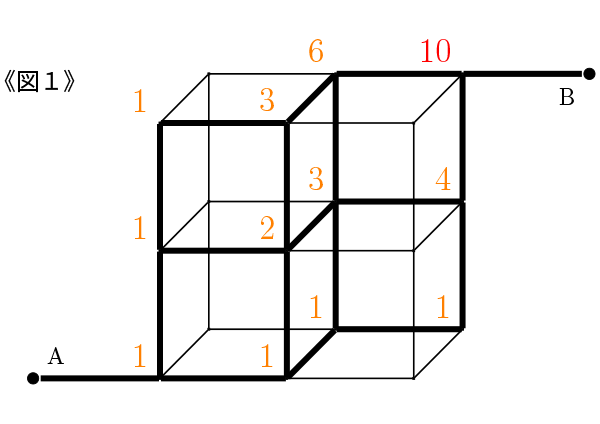
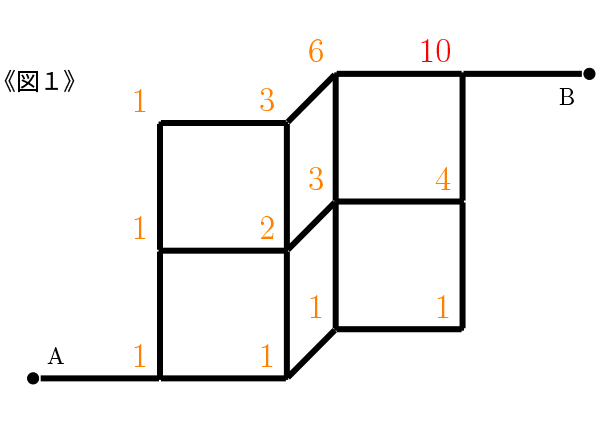
答えは　　《図１》　１０通りです。

【道順　解法：交差点に本数を書いていく　立体図形版】　

《図２》の立体図形は、３本の直線が集まっている交差点があるので、数え方に注意しましょう。

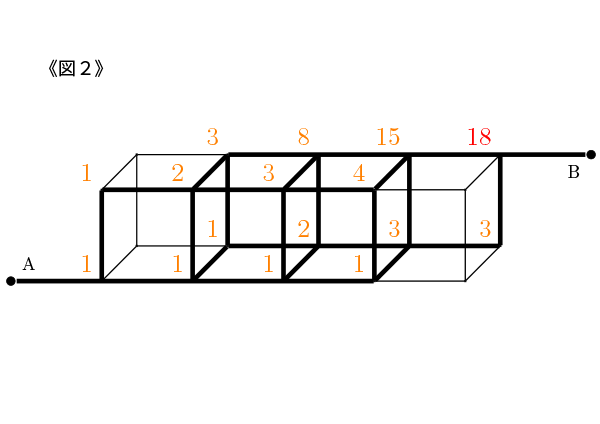
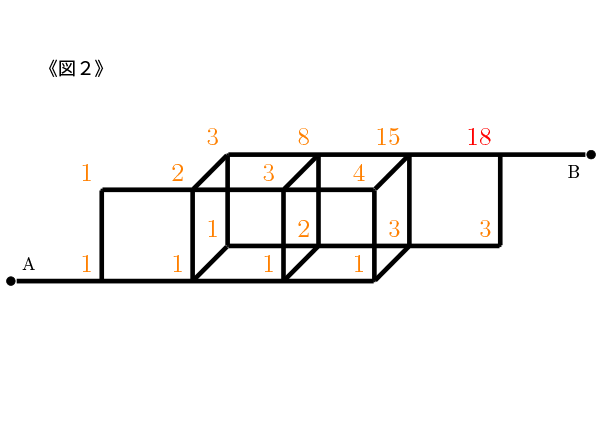
答えは　　《図２》　１８通りです。

【解説続き　原記事】