自然という書物は数学の言葉で書かれている。目に見える自然、目に見えない数学。虚数単位iは共感力。

５月５日（水）

ご覧いただきありがとうございます(^O^)
高校教師（宮城県）を退職し、全国のデモクラティックスクール、

北欧デンマークの教育を学んだ後、仙台から教育革命をしている伊藤真結です。

公式ホームページはこちら≪ Mayu Academia ≫
２０２０年４月からAKIU SCHOLĒ（アキウスコレー）という
新しい学校🏫を仙台市秋保町に創っています。

全日制の学校に行っていても、通信制高校に行っていても、不登校でも。
全ての中高生が、自分の選択で自分の人生を切り拓く力を育みます。
伊藤真結の応援はこちらから≪🎪 MAYU’s SCHOLĒ 🎪≫

詳細はページ下へ。

【社会起業家育成プログラムTOHOKU SOCIAL INNOVATION Acceleratorプログラム2019】
「共感賞受賞」最終プレゼン動画：https://www.youtube.com/watch?v=ieW27hLim5c

聴くブログはこちらから→聴くブログ

今日は朝から、

もはや家族みたいな大親友と久しぶりに会って、

その子どもたち、一番上の子はもう小学５年生、

とたわむれて、

最高に癒された１日です。

母と松島にドライブに行って黄昏たり、

有難く平和なゴールデンウィークも終わりを迎えようとしています。

ゴールデンウィークと言えど

仕事と休みの境目のない感じです。

今日は数学の勉強をしていました。

特に虚数単位 i の勉強が面白くて、

私の高校の時には教科書に入っていなかった「複素数平面」が数学Ⅲに入ってきて、

数学Ⅱで虚数を学んだなら、是非数学Ⅲで複素数平面まで学ぶと良いなあ、

なんて思っています。

大学でフルで数学を学べなかったことは事実で、

だからこそ、まだまだ、数学は知らないことだらけで、

日々、勉強しています。

学ぼうと思ったら、

ゼロ円で一生学び続けられる現代に感謝です。

▽

虚数単位 i のことを、

「ああ、そんなのあったね！」

「今もばりばり使っています」

という人が日本にどれだけ居るのかは分かりませんが、

将来何の役に立つのかと言われる数学という学問は、

それこそ人工的なものではなくて、

人間が手を加えてきたものでは無くて、

自然の中に成り立つものです。

有名なガリレオ・ガリレイさんが残した言葉の中には、

「自然という書物は数学の言葉で書かれている」

というものがあります。（かっこいい・・・。）

だからそこには、

難しさや、役に立つとか立たないとか、

そういうものを越えて本質的に大事な真理が、

たくさん詰まっていると、いつも感じます。

▽

例えば、

フィボナッチ数列、というとっても有名な数列があります。

自然界に多くみられる数列～フィボナッチ数列～
イタリアの数学者フィボナッチ(1170~1259年頃)が紹介した数列を「フィボナッチ数列」と言います。

１、１、２、３、５、８、１３、２１、３４、５５、８９、１４４、２３３、３７７…

「どの数字も前２つの数字を足した数字」という規則の数列です。

自然界と人体の神秘 ～フィボナッチ数列、黄金比から垣間見える～

１，１，

１＋１＝２

１＋２＝３

２＋３＝５

３＋５＝８

５＋８＝１３・・・・

といった風に、数が紡がれていきます。

自然界には、フィボナッチ数列がたくさんあります。

数学者のフィボナッチは「ウサギの増える」様子をみて、この数列を見つけたそうです。

子ウサギを観察し、

1か月には大人(１つがい)になり、

2か月後には子ウサギを産んで2つがいになりました。

3か月目には３つがい、4ヶ月目には５つがい、

5か月目には８つがい、

ウサギは「１、１、２、３、５、８．１３、…」と増えることを観察しました。

フィボナッチさんすごいです( ˘•ω•˘ )。

他にも、

ほとんどの木はフィボナッチ数列によって「枝分かれ」していくそうです。

よくよく見ると人体の「気管支の枝分かれ」や「肝臓の血管の枝分かれ」も同様に分岐しています。

まさに、

「自然という書物は数学の言葉で書かれている」

ということで、

自然界に起きていることを、

数で解いています。

で、

すごいのが、

この数列の、一般項（第ｎ番目に、どんな数が来るのかをｎで表すこと）なんです。

▽

フィボナッチ数列は少し複雑なので、

一般項の説明をここで簡単にさせて頂きます。

例えば

２，４，６，８，１６，３２，・・・・・

という数列があったとします。

１番目は２．

２番目は４．

３番目は６，

４番目は８，

・・・・

では、１０番目は何になると思いますか？

この時、１０番目まで数を書き上げるのもひとつですが、

これが、じゃあ１６２番目は？

となると、

書き上げるのはちょっと面倒です。

ここで出てくるのが、一般項です。

この場合偶数の数列という簡単な数列なので、

１０番目は、２×１０＝１０

１６２番目は、２×１６２＝３２４。

と簡単に出せたと思います。

「〇番目の数」と、〇との関係が、一般項です。

〇番目の数は、

２×〇

になります。

よって、

２，４，６，８，１６，３２，・・・・・

の第ｎ番目の数は、２ｎと表されます。

一般項は、２ｎです。

▽

フィボナッチ数列の話に戻ります。

１、１、２、３、５、８、１３、２１、３４、５５、８９・・・・

前二つの数を足し合わせて出来るフィボナッチ数列は、

正の整数の足し算なので、

１００番目でも、１０００番目でも、その数は、整数になります。

でも、

目に見えている

正の整数の数列の第ｎ番目を表すためには、

正の整数だけでは、

表せないんです。

なんと、

正の整数の数列の第ｎ番目を表すと、

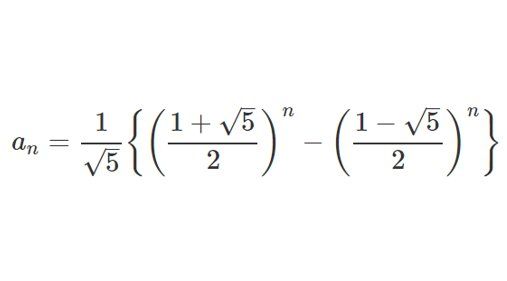
こうなるんです。

そうです、

みんな知ってる√ルートす。

無理数

です。

無理数とは、分数に表すことのできない数（実数）です。

正の整数の数列の、第ｎ番目を表すのに、

正の整数では事足りないんです。

無理数、√が無ければ、

表現できないんですね。

目に見える「数」を表すのに、

目には見えない「数」が必要なんです。

▽

更にこれと似た、

トリボナッチ数列っていうのもあって、

トリボナッチ数列はもっとぶっ飛んでます。

トリボナッチ数列は、

 

０，０，１，１，２，４，７，１３，２４，４４，８１，１４９，２７４，５０４，９２７，１７０５，・・・

 

といった整数の数列で、

前3つの数字を足した数列です。

このトリボナッチ数列もまた、

整数の数列ですが、

この数列の一般項には、

なんと、

虚数 i が出てくるんです・・・・・・・。

トリボナッチ数列の一般項は、

ちょっとここに記載するのが大変なので割愛します。(笑)

https://mathlog.info/articles/291

虚数単位 i って、

イマジナリーナンバーと言って、

空想上の、想像上の数と言われています。

それくらい、

妄想みたいな数なんだけど、

妄想と言われようが、空想上のと言われようが、どこまで行ってもそれは、

自然という書物は数学の言葉で書かれていて、

人が作ったのではなく、人が、見つけたものであり、

その数が“ある”から、表現できることが存在するのは、確かだという、

ドキドキするお話です。

目に見えているものを表すのに、

目には見えない無限に広がった数学の世界で考える必要があるんです。

▽

数学だけでなく、

人とのコミュニケーションでも、なんでもそうかもしれないです。

目に見えているものを理解するためには、

目に見えている事だけでは足りなくて、

その他に色んなことを考える必要があります。

これが、人間に備わっている「共感力」だったりするなああ、

と私は思っていて、

これがまさに、

虚数単位 i と似ているなあ、と感じました。

虚数単位 i は、「共感力」みたいなものです。

複素数平面では、この i の動きがとても面白くて、

 i が共感力であるならば、複素数平面は心理学みたいなものかな、

なんて考えていました。

▽

そんなゴールデンウィーク最終日でした。(笑)

数学、もっと勉強します。がんばります。