FomoJP。数学的な側面からの分析②～詳細版～

はじめに

この記事は第1部で分析した内容をより興味のある人のために、数式などを用いてどのような方法で分析を行ったのかを解説していく。

そのため、第１部の内容の補足説明を主な目的としているため、計算過程などを詳しく知りたい人向けの記事となる。

ゲーム性についての分析結果のみを確認したい場合は第１部の記事を参照されること。

この第２部では特別に新しい情報を追加しているわけではない。

第1部はこちら

目次

・おさらい

・n本目のkeyの値段

・n本目からm本目までのkeyの値段

・n本目のkeyが購入されたときの所有key１本当たりの配当

・n本目からm本目のkeyが購入されたときの所有key１本当たりの配当

・m本目までkeyが購入されたときn本目のkeyの資金回収率

おさらい

前回の記事のおさらいとして、この先計算していくのに必要な情報をもう１度まとめておく。

・1本目のkeyの値段：0.000075 ETH/本

・n番目のkeyの値段：0.000075 + (1.5625E-10 x (n-1)) ETH/本

・配当に回る金額はkeyの値段の56%

・配当はkeyの保有比率に応じて均等に分配される

全ての計算はこの４つの情報からのみ考えていく。

また、この4つの条件はスマートコントラクトのコード内から確認した内容であるため、最初から与えられている情報である。

では、この情報を利用して目次の順番に沿って解説していく。

n本目のkeyの値段

keyは１本購入される度に約1.5625E-10 ETHだけ値段が上昇するため直線の式

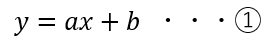
で表すことができる。

このとき、１本目のkeyの値段と上昇する値段がわかっているため

y = 0.000075

x = 1

a = 1.5625E-10

をそれぞれ①に代入してbを求めることができる。

そのときのbの値は

b = 7.499984E-5

となる。

したがって、n本目のkeyの値段は

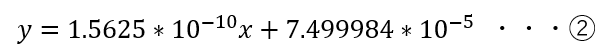
で表せる。

ここで係数aおよびbは毎回数値を代入すると見づらくなるため、以降は代入せずに文字で表す。

②の式をグラフにすると第1部の記事でも紹介した下のグラフが描ける。

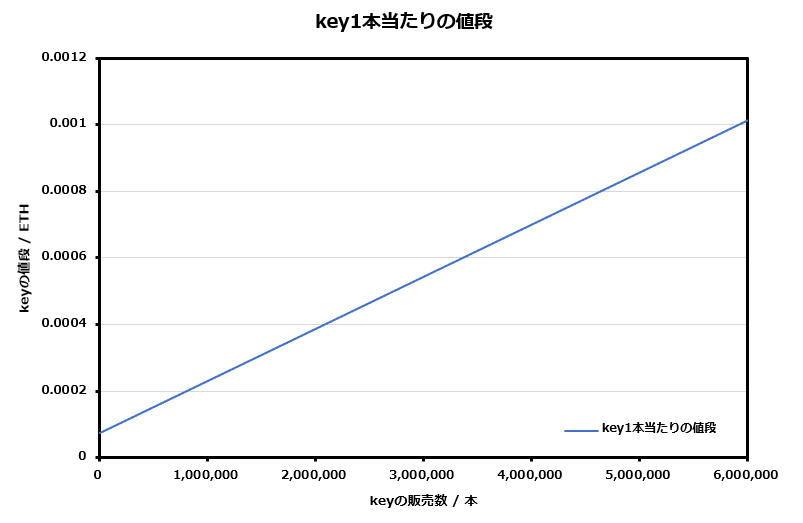
n本目からm本目までのkeyの値段

次に複数のkeyをまとめて買うときの値段を考える。

これは既にkey1本当たりの値段がわかっているため、②の式を積分することで求めることができる。

積分すると、式③が得られる。

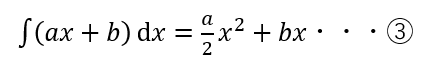
今回はn本目からm本目のkeyの値段を知りたいので③の式から

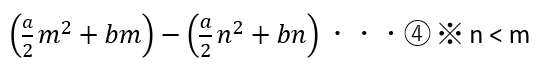
④が計算できる。

これを解くと、n本目からm本目までのkeyをまとめて購入した金額となる。

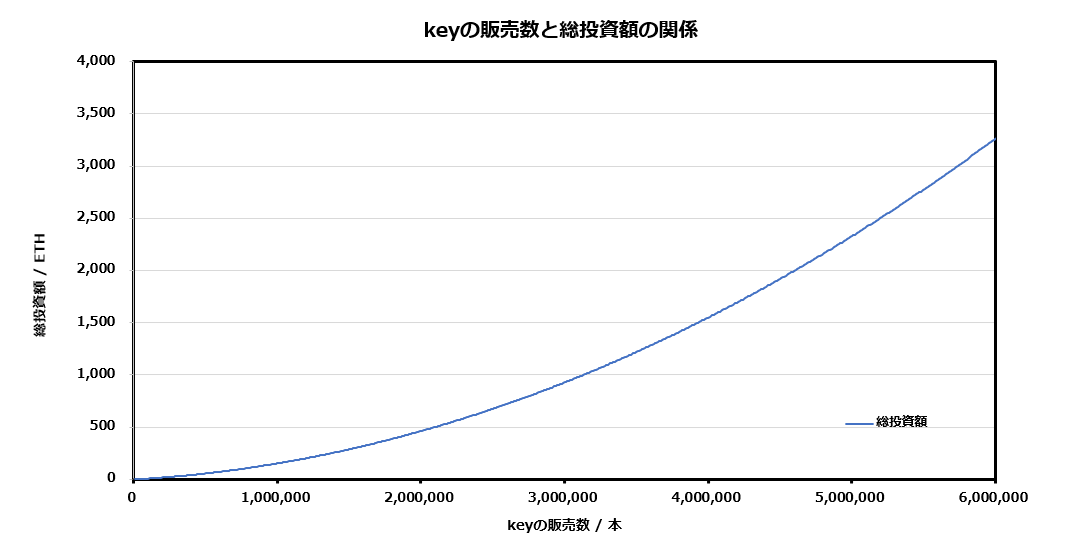
また、このときにn＝0とするとm本目までの総投資額を求めることができ、下のようなグラフを得る。

n本目のkeyが購入されたときの所有key１本当たりの配当

１本当たりのkeyの配当は

0.56　*（購入されたkeyの値段　/ 販売済みのkeyの本数）

で求めることができる。

ここでn本目にkeyを購入したと考えると、購入されたkeyの値段は式①となり、販売済みのkeyの本数は(n-1)本となる。

したがって、n本目のkeyが購入されたときの所有key1本当たりの配当は

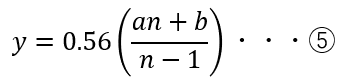
で表される。

ここで、nが十分大きいとき

1/(n-1) ≒ 1/n

となるため、式⑥に近似することができる。

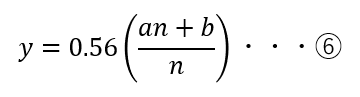
しかし、nが小さいときは誤差が発生してしまうが、ここではこれ以降の計算を簡単にすることを優先する。

この式⑥を変形することで

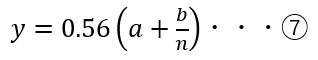
key1本当たりの配当を表す式⑦が得られる。

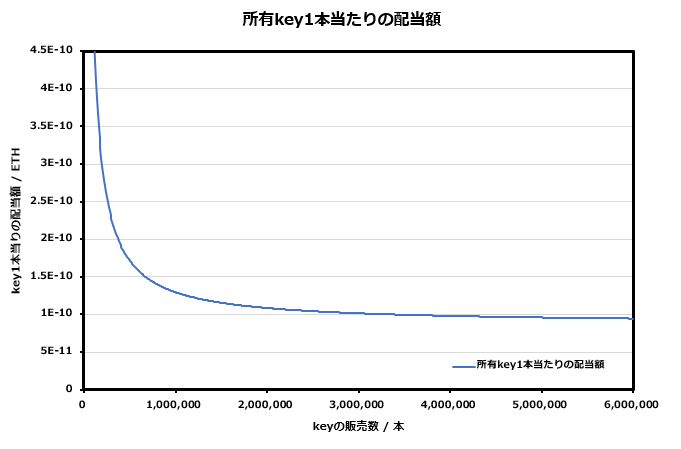
式⑦を見てわかるように、nが非常に大きくなると

b/nが限りなく0に近づくため、配当は限りなく0.56aに近づいていく。

これが先行者優位を加速させている重要な仕組みである。

グラフで表すと前回の記事でも紹介した下のグラフが得られる。

n本目からm本目のkeyが購入されたときの所有key１本当たりの配当

これはn本目からm本目までの複数のkeyを買うときと同様の考え方で計算することができる。keyが1本購入されたときの配当を表す式⑦をすでに求めているので、これを積分すればよい。

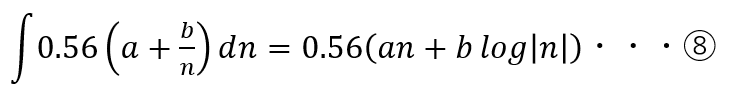
したがって、n本目からm本目のkeyが購入されたときの配当は次式で表される。

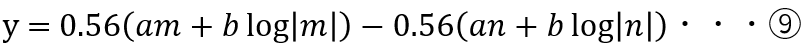
このとき、1≦n<mの関係性がある。

さらに、この⑨式を使うことで、n本目に買ったkeyがいつ原資回収できるかを簡単に求めることができる。

⑨式の左辺のyをn本目のkeyの値段である①式を代入して式変形すると、

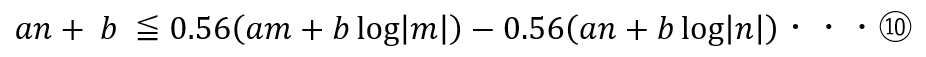
⑩式が得られる。

この式を満たすmがn本目に買ったkeyの原資を回収している状態を示す。

m本目までkeyが購入されたときのn本目のkeyの資金回収率

この資金回収率も式⑨を用いれば、簡単に求めることができる。

まず、n本目に買ったkeyがm本目までに貰える配当は式⑨そのものであり、その配当額をn本目のkeyの値段で割れば良い。

ここで、資金の回収率をLとおくと、次式で表される。

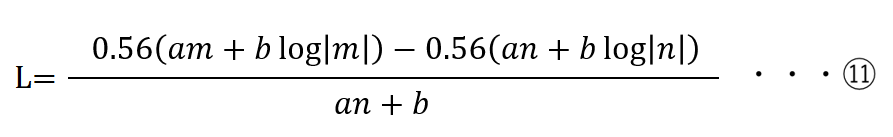
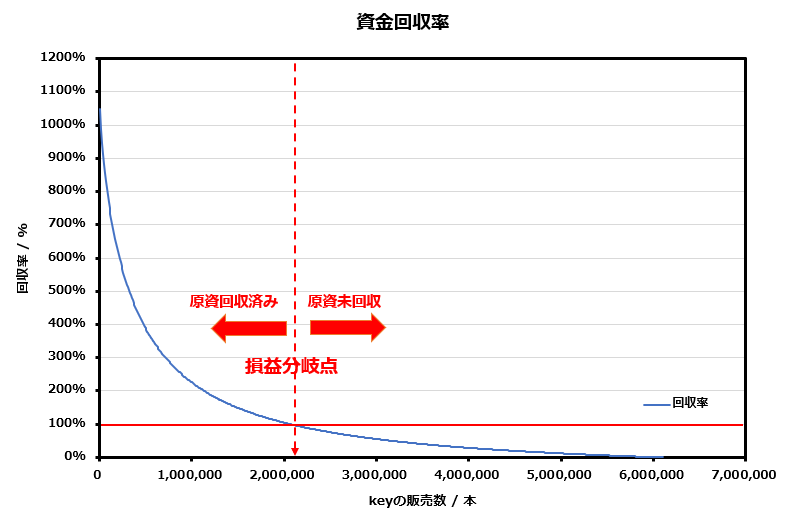
この式を用いて、m = 610万としてn = 1, 2, 3・・・と順に計算していくことで、前回の記事で紹介した下のグラフを描くことができる。

おわりに

以上が今回の記事で計算に用いた代表的な数式となる。

ゲーム性が乏しく大量の資金が投入されるような多くの投機系のイベントは、このように特殊な構造を持ちどこかの層に集中的に資金が集まるような設計になっているものを見かけることが多い。

このようなイベントに参加するのは個人の意志に委ねられているが、その特殊な構造を理解せずにリスクを甘くみて参加すると予想以上のお金や時間を失うことがある。

この記事によって、１人でも多くの人のそのようなお金や時間を無駄に失う機会を減らすことができれば幸いである。

おまけ

普段はLINE＠を利用して、このようなdAppsゲームの情報を中心に不定期配信を行っています。

興味のある方はご登録をお願い致します。

https://line.me/R/ti/p/%40lgj4004p

また記事が参考になった方は「いいね」あるいは「ETH」の投げ銭をしていただけるとモチベーションアップになりますのでよろしくお願い致します。

投げ銭用アドレス

0x757448a6e4BDBF280b21e042Eb86501E2dCbDB5d