FomoJP。数学的な側面からの分析① ~簡易版～

はじめに

本記事は最近話題になっているFomoJPのゲーム性を数学的な側面から分析することによって、どのような性質のゲームかをよりわかりやすくし、先行者優位が強調されているが実際はどうなのかを調べることを目的としている。

この記事では単に分析した事実をまとめているだけであり、FomoJPのような仕組みを推奨するわけでもなく、批判するわけでもない。

記事は二部構成を予定しており、まずはこの第一部の記事を簡易版としてできるだけ数式を使わずにゲーム構成が大まかにイメージできるようなザックリとしたまとめを用意した。

第二部の記事でより興味のある人のために数式などを用いて詳細な解説を用意しようと考えている。しかし、数式を用いた説明は思っていたよりもかなりの労力がかかりそうであるため第二部の記事は書くかどうかは検討中である。

それでは、最低限の前提条件から説明していく。

前提条件

できるだけ複雑な計算を避けるために、いくつかの前提条件を設けることで本質的なゲーム性を崩さずにシンプルなモデルを考えた。

以下が前提条件である。

・ジャックポットは発生しない

・第2ラウンドはやってこない

・チームはスネークのみ

この条件に加えて、計算途中の値の丸め込みや数式の近似によって実際と比べて多少の誤差が発生するがゲーム性を理解する上では無視できる範囲で収まるように計算は実施している。

具体的な計算式などは第二部で解説予定であり、第一部では特に説明しない。

基本情報と現在の状態（8月24日現在）

ここではゲームのイメージを掴みやすくするために、基本情報と現在のゲームの進行状態をまとめる。

・参加プレイヤー数：1272 ウォレット

・販売key数：6,106,685 本

・総投資額：3371.4 ETH

・現在のkeyの値段：0.001029 ETH/本

・1個目のkeyの値段：0.000075 ETH/本

・n番目のkeyの値段：0.000075 + (1.56E-10 ☓ n) ETH/本

・配当に回る金額はkeyの値段の56%

・配当はkeyの保有比率に応じて均等に分配される

では早速、分析結果に移っていく。

①key1本の値段について

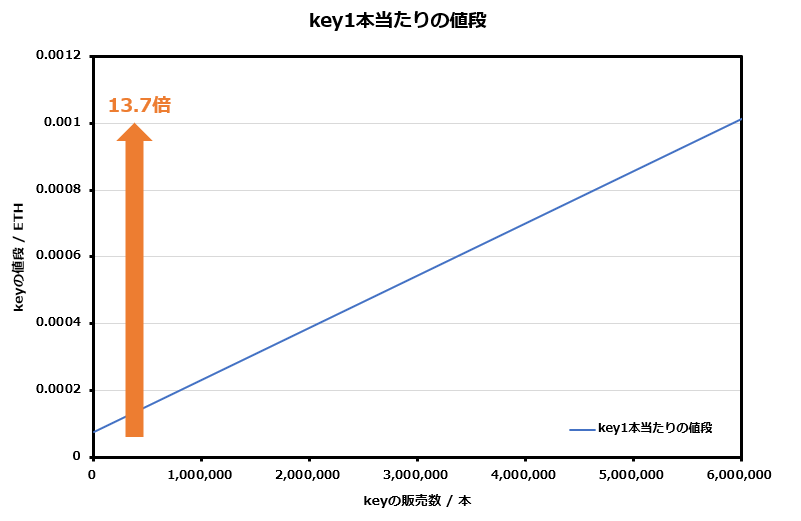
key1本当たりの値段は販売される度にグラフのように直線的に価格が上昇する。

1本目のkeyの値段は0.000075 ETHで、keyが1本売れるごとに

約0.000000000156 ETH価格が上昇する。

現在は約600万本のkeyが販売されているため、その販売値段は

約0.001029 ETHである。

これは初期価格の約13.7倍の値段が付いていることになる。

この時点で単純に考えても、初期の頃にゲームに参加した場合と今からゲームに参加した場合で投資効果が13.7倍近く違うと考えることができる。

つまり、key1本当たりの値段を考えただけでも、かなり先行者優位が働くであろうことがわかる。

また、自分が何本目に販売されたkeyを購入したのかは購入金額から、ここに示されているグラフを利用して概算すると楽に求められる。

②key一本当たりの配当

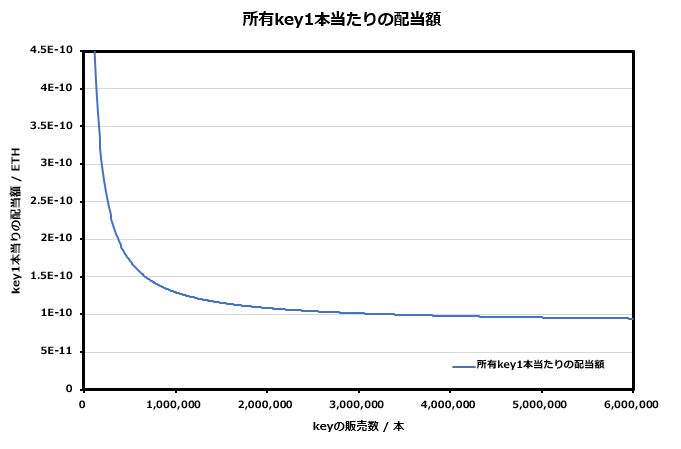
次は配当について。

グラフは所有key1本当たり何個目のkeyが売れたときに、どのぐらいの配当が手に入るかを表している。

縦軸の目盛りは先程のグラフよりもかなり小さいので注意。

配当に関してはkeyの値段のような直線的なグラフではなく、曲線で推移する。

これはkeyが購入され配当が発生した際に、すでに販売されたkeyが大量にあるとその分だけ配当が分割されるため、販売数が増えると配当が貰えにくくなるためである。

ちなみに、現在のkeyの販売数は約600万本なので1本購入される度に、所有key1本につき

約0.0000000001ETHの配当が得られる。

またグラフからkeyの販売数が100万本付近を目安に、これよりも販売数が少ないときは今と比べて高い配当が貰えていたことがわかる。

このグラフには縦軸の関係でkeyの販売数が12万本を超えたところからしか描かれていないが、特にkeyの販売数が10万本よりも少ないときはkey１本当たりから得られる配当の額は今とは比較にならないことがグラフからも想像できる。

もちろん配当額が一定であったと考えた場合であっても、keyを早く購入することはそれだけ配当を得られる機会が増えるので先行者優位が働く。

今回のこのグラフは100万本よりも少ない段階でkeyを購入しておくことで、その配当が貰える機会の増加に加えて配当額そのものも非常に大きかったことを表している。

これは①で考えたkeyの値段の上昇と合わせることで、とてつもないほどの先行者優位が働くことが容易に推測できる。

ちなみに、keyの販売数が100万本に到達するのは総投資額が約153ETHのときであり、10万本に至っては総投資額約8.3ETHで到達する。

今の総投資額3371ETHから考えると、全体の0.25%に当たる最初の8.3ETHが驚くほどの先行者優位を獲得し、全体の4.5%に当たる最初の153ETHの投資が先行者優位の恩恵を十分に受けたと考えられる。

③回収率について

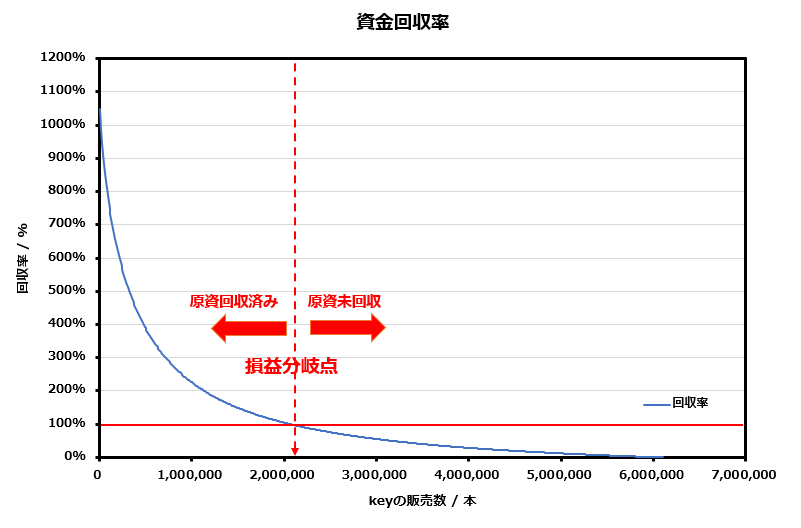
こちらは想定される現時点での実際の回収率について。

グラフを見てわかる通り、損益分岐点よりも前でkeyを購入していれば利益が出ている。

そして、②の配当の項目で述べたように購入が早ければ早いほど驚くほどの先行者優位を獲得するので、回収率のグラフも曲線を描く。

このグラフについては特に説明することはないだろう。

この記事の目的である先行者優位の実際そのものをグラフに表したようなものだからである。

では、続いて実際にいくつかのシミュレーションを想定することによってもう少し深くゲームを理解することを試みる。

シミュレーション①

610万本のkeyが販売されたとき、配当だけで利益を出すためには何本目までのkeyを購入しておく必要があるのか。

ここでは詳細な解説を省くが、答えは約205万本目までである。

これは総投資額にして約482ETHのときに到達する。

つまり、現在の総投資額3371ETHから考えると全体の約14.3%で利益が出ていることになる。

したがって、この結果からジャックポットを無視した場合、現時点では全体の14.3%が先行者優位があるといえる。

また、その先行者優位の度合いは早く参加すればするほどとてつもなく大きくなる。

シミュレーション②

では、その先行者優位の度合いを感覚的に掴むために２パターンの先行者の利益について計算する。

パターン１：150万本目から1ETH分のkeyを購入した場合

この場合だとkeyは約3200本購入することができる。

そして現在と同じ610万本目までkeyが販売されたときの配当を求める。

配当金額は約1.48ETHになり、回収率は148%となる。

パターン２：10万本目から１ETH分のkeyを購入した場合

この場合だとkeyは約11000本購入することができる。

パターン1と比べてkeyの値段が安いため同じ資金で3倍以上購入できる。

そして、パターン１と同様に配当額を求めると

配当金額は約7.67ETHになり、回収率は767%となる。

この２つのパターンからわかるように先行者でも、その恩恵の受け方は大きく異なりより早くゲームに参加した方が圧倒的な恩恵が受けられることがわかる。

結論

先行者優位が強調され話題になったFomoJPであったが、その先行者とは全体の約15%程度のことを指しており、その優位性はより早く参加すればするほど曲線的に増加するといえる。

ただし、この結果はジャックポットなどの一部の条件を無視して分析しているため配当による利益のみを目指したときにのみ適用される。

第2部はこちら

おまけ

普段はLINE＠を利用して、このようなdAppsゲームの情報を中心に不定期配信を行っています。

興味のある方はご登録をお願い致します。

また記事が参考になった方は「いいね」あるいは「ETH」の投げ銭をしていただけるとモチベーションアップになりますのでよろしくお願い致します。

投げ銭用アドレス

0x757448a6e4BDBF280b21e042Eb86501E2dCbDB5d