完全に理解したのsupporting information

前の記事から

7) までの式を抽象度を高めるため, depositするときの相場価格Piに対して, 現在価格P=rPiと置き、変動率rとILの関係曲線を示す。気が向いたら各自rおよびPmax=MPi, Pmin=mPiと置いたときのM, mを使って7)の式を変形してみてほしい.

実際にやってみた(形はそんなに簡単にはなりません, 価格Pが消えてそれぞれの倍率で表現できるようになる程度です)

7-1) depositするときの価格がレンジの下限より小さいとき(1<m)のIL

7-1-1) 1<m, 現在価格もレンジの下限以下(r<m)のとき

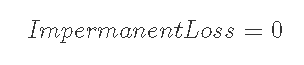
7-1-2) 1<m, 現在価格がレンジの上限以上(M<r)のとき

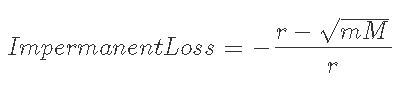
7-1-3) 1<m, 現在価格がレンジ内(m<r<M)のとき

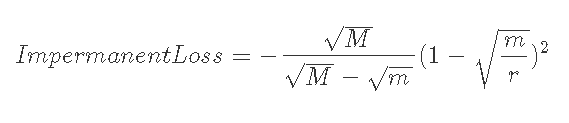
いずれにおいてもIL≦0

7-2) depositするときの価格がレンジの上限より大きいとき(M<1)のIL

7-2-1) M<1, 現在価格がレンジの下限以下(r<m)のとき

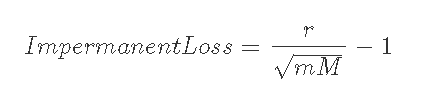
7-2-2) M<1, 現在価格がレンジの上限以上(M<r)のとき

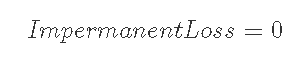
7-2-3) M<1, 現在価格がレンジ内(m<r<M)のとき

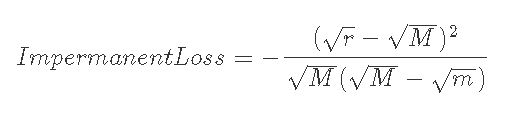
いずれにおいてもIL≦0

7-3) depositするときの価格がレンジ内(m<1<M)のとき

7-3-1) m<1<M, 現在価格がレンジの下限以下(r<m)のとき

7-3-2) m<1<M, 現在価格がレンジの上限以上(M<r)のとき

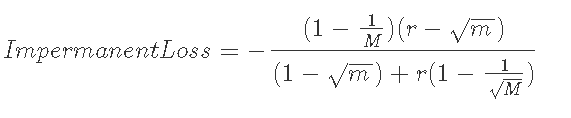
7-3-3) m<1<M, 現在価格がレンジ内(m<r<M)のとき

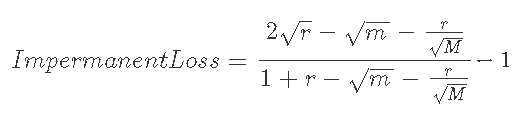
m→0, M→∞, 1/M→0とすると、見慣れたILの式になる

いずれにおいてもIL≦0

こっちの方がPriceを使わないので概念的に理解しやすいかもしれない。