算数 de アルゴリズム －つるかめ算－

初めに

小学校にプログラミング教育が導入される時代である。

そこで、受験算数とプログラミングを合わせたカリキュラムを提案していこう。

と、いうことを考えてみた。

受験算数は方程式を使わないで解くという暗黙の了解があるため、アルゴリズムについて考えることと親和性がある、・・・ような気がする。

さらに、受験算数もアルゴリズムも、大人が趣味で考えるのに程よく面白い、と僕は思っているので、是非興味を持ってもらえればと思う。

そんな訳で、第１回は「つるかめ算」を扱ってみよう。

問題：

ツルとカメがいます。頭の数は合わせて60、足の数は合わせて192本です。
 

ツルは何羽いますか？

①　ごり押しアルゴリズム

全く何も考えないで、１羽から順番に計算して解こうということだ。

ツルが１羽なら、1×2+59×4＝238

ツルが２羽なら、2×2+58×4＝236

ツルが３羽なら、3×2+57×4＝234

　　　　・　　　　　　・
　　　　・　　　　　　・
　　　　・　　　　　　・

ツルが24羽なら、24×2+36×4＝192

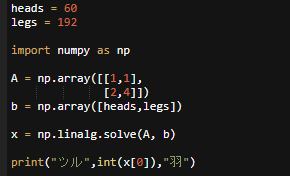
　　　　　　　　　　　　　　　　　　　　　A　ツル 24 羽

まあ、繰り返せばそのうち答えは出る。

プログラムにしてみよう。

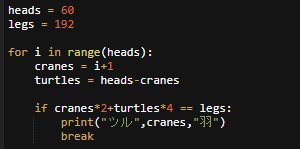
わかりやすさを優先して、やや冗長に書いている。

②　つるかめアルゴリズム

つるかめ算にはちゃんと解法があるので、それを使ってみる。

60匹全てカメだったと仮定すると足の数は、60×4＝240本

実際は192本なので、240-192＝48本、足が多い。

ここで、カメを１匹取り出し、代わりにツル１羽を加えることを考えると、

足の数が、４➡２、となり２本減る。

よって、48÷2＝24、カメを24匹取り出し、ツルを24羽加えれば良い。

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　A　ツル 24 羽

受験算数的には、ツルは？と聞かれたら、逆の全部カメから始めるというところがポイントだ。全部ツルで始めても解けるが、カメが求まってしまうので、最後に１回引き算を余計にすることになり時間が無駄だ。

プログラムにしてみる。

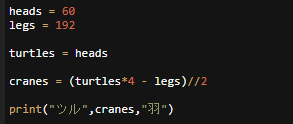
わかりやすさを無視すれば、

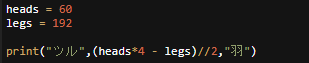
１行で良い。

さて、どう考えても②の方が計算が楽なのは確かだが、実行時間を比べてみよう。

コンピュータ君は非常に計算が早いから60匹程度では差が出ないので、

ツルとカメがいます。頭の数は合わせて6000000(600万)、
足の数は合わせて192000000本(1920万本)です。
ツルは何羽いますか？

こいつを計算させてみる、

①

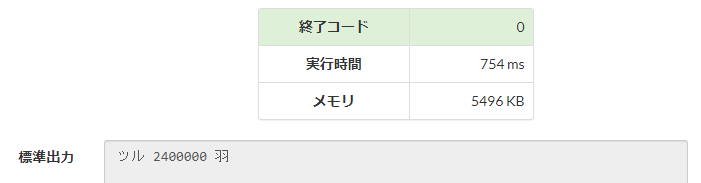
②

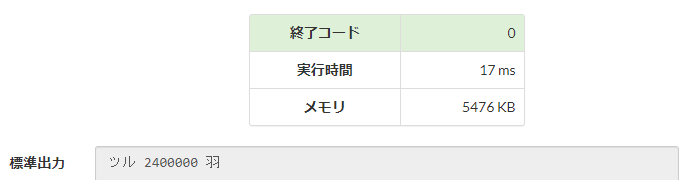
②の方が44倍速い、これがアルゴリズムを考える意義だ。

③　ごり押しアルゴリズム×二分探索

つるかめアルゴリズムは簡単なのですぐに思い浮かぶが、仮に思い浮かばなかったとしよう。良いアルゴリズムは思いつかないが、ごり押しよりは早く計算したい。

そんなときの為に二分探索というアルゴリズムがある。

ちなみにこれは算数の世界ではなくプログラムの世界で使われるアルゴリズムだ。

前から順番に計算するのではなく、真ん中を計算していくというもので、

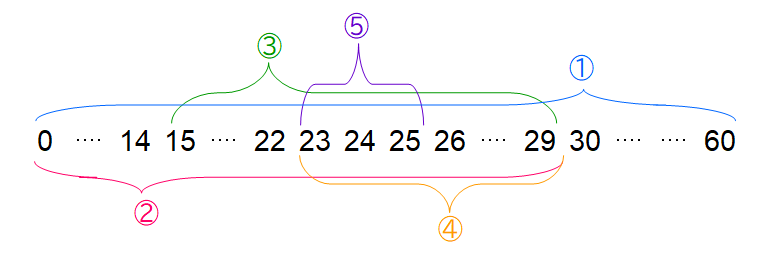
１、0～60の真ん中、30羽を計算する、30×2+30×4＝180本

　　足が192本より少ないということはツルの数は30羽より少ないはずだ。

２、0～29の真ん中、14羽を計算する、14×2+46×4＝212本

　　足が192本より多いということはツルの数は14羽より多いはずだ。

３、15～29の真ん中、22羽を計算する、22×2+38×4＝196本

　　足が192本より多いということはツルの数は22羽より多いはずだ。

４、23～29の真ん中、26羽を計算する、26×2+34×4＝188本

　　足が192本より少ないということはツルの数は26羽より少ないはずだ。

５、23～25の真ん中、24羽を計算する、24×2+36×4＝192本

　　足が192本、これが答えだ。

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　A　ツル 24 羽

１から順番に計算した場合24回の繰り返しが必要なところ、５回の繰り返しで答えを求めることが出来た。

プログラムにしてみる。

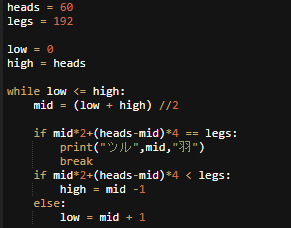
600万匹の実行時間は、

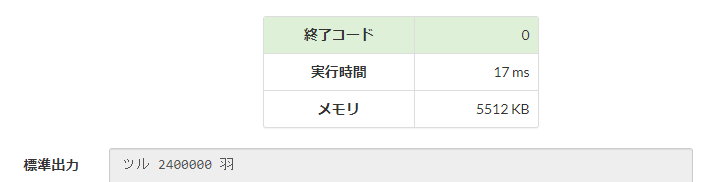
なんと、つるかめアルゴリズムと同等の速さになった。

もっと多くなれば遅くなるかと思ったが、600億匹になっても同じ時間で出せる。

つまり、つるかめ算の解法を知らなくても二分探索を使えればゴリ押しで勝負を挑めるということだ、まあ手計算の勝負なら完敗するに違いないが。

④　おまけ　連立方程式

つるかめ算は中学生なら連立方程式を使って解くことも出来る。

ツルを x 羽、カメを y 匹とする、

　　x+y=60
　　2x+4y=192

            　x=24

　　　　　　　　　　　　　　　　　　　　　A　ツル 24 羽

プログラムにしてみる。

600万匹の実行時間は、

なんと遅い、

ごり押しよりは早いが、つるかめアルゴリズムや二分探索よりは遅い。

これ実は手計算でも同じことが言えて、つるかめアルゴリズムを極めている小学生に大人が連立方程式で勝負を挑んだ場合、まず勝てない。

その辺が受験算数の面白いところでもある。

最後に

さて、受験算数とアルゴリズムとプログラミング、興味を持って頂けただろうか。

これ書くのにめちゃめちゃ時間掛かっているので少しでも面白いと思ってもらえると嬉しいのだが、この手のものはどうなのか微妙なところだ。

ちなみに、つるかめ算は特殊算と呼ばれるもので、他にも有名なところで植木算、旅人算なんかがある。ということは、他のものも書けるのだが、後は誰が読んでくれるのかという問題だ。

宿題

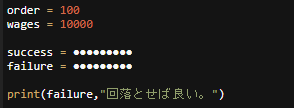
貴方はドジっ子メイドカフェでアルバイトをしています。

ご主人様にコーヒーを１杯運ぶと200円もらえます、しかし貴方はドジっ子メイドなので数回に一度は運んでいる途中で落とさなければなりません。

運んでいる途中で落としてしまうと200円がもらえないばかりでなく、店長さんに800円を支払わなければなりません。

コーヒーを落とさなければ稼ぎは多くなりますが、ドジっ子メイドのキャラが立たないので、可能な範囲でなるべくたくさん落とさなければなりません。

貴方がコーヒーを100回運んで10000円稼ぎたいと思っている場合、100回のうち最大で何回コーヒーを落とすキャラを演じれば良いでしょう。

細かい分類だと弁償算と呼ばれることもあるが、つるかめ算の一種だ。

もちろん①～④どの解法でも解くことが出来る。

１、　答えを求めよ。

２、　success、failure に入るものを答えよ。
 　　　ただしsuccessはちゃんと運ぶ回数、failureは落とす回数を表すものとする。