


katakotoさん から依頼を受けたので考えてみた。

依頼内容をまとめると
「ハッシュ関数の強衝突耐性を皮膚感覚で実感したい。」
ということのようだ。
「面白おかしく」
の部分は見なかったことにする、この話題でそれは無茶振り過ぎる。
これは非常に難しい、大きな数というのは往々にして皮膚感覚で実感しにくい、例えば 233,280 ㎡ と言われてもよくわからないので、東京ドーム5個分と言われるような感じだ。しかし今回の話はそんなレベルではない、2の256乗という話だ。
途中で面倒になって放棄しようかとも思ったのだが、かなり頑張って皮膚感覚に沿うような例えを考えてみた。ハッシュ関数などについての説明は間違っているかもしれないが、その辺の厳密な話は今回は置いておくことにする、その辺を知りたい方は別のところで調べてもらった方が良い。
問題:
ここに本が1冊ある、適当にページをめくって、そのページの一番初めに書いてある文字をメモするものとする。
(これがハッシュ関数。何の本の何ページ目か言えば初めの一文字を出せるが、
初めの一文字から何の本の何ページか逆引きするのは無理だ。)
このとき初めの1文字が同じであるページの組を見つけるには何回ページをめくれば良いだろうか。(同じハッシュ値を返すページを見つけようとしている。)
(ただし文字は全てひらがなで、ひらがなは50種類あるとする。)
答え:
9回適当にページをめくれば初めの1文字が同じ組が見つかる確率が50%を超える。
17回めくれば97%の確率で初めの1文字が同じページの組が見つかる。
50種類もあるのに意外と早く同じ文字が2回出てくるな、と思っただろうか。試しにその辺にある本でやってみて欲しい、僕は4回目で出てくる文字が被った。
これを「誕生日のパラドックス」というそうだ、この意外と早く同じ文字を返すページの組が見つかることを利用したハッシュ関数への攻撃を「誕生日攻撃」という。
そして、誕生日攻撃に耐えられるかどうかを強衝突耐性というらしい。
ちなみに答えを出すための確率の計算はこうなる、
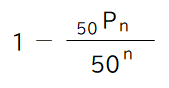
何でこうなるかは省略、数Aの教科書を見て欲しい。
ちなみに予め探す文字を指定し、その文字と一致するページを探すとなると、各段に大変になる。こちらの方法での攻撃に耐えられるかどうかを弱衝突耐性という。
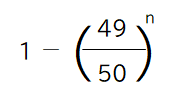
計算法はこうで、
35回で、その中に探したい文字で始まるページを含んでいる確率が50%を超える。
180回で97%になる。
これは上とは逆に思ったより見つからないものだ。
話を戻して、この場合たった17回ページをめくっただけで、同じ文字で始まるページ1組を 97%の確率で特定されてしまう、強衝突耐性は全くないと言って良いだろう。
では、初めの2文字にしたらどうだろうか、
問題:
初めの2文字が一致するページの組を見つけるには何回ページをめくれば良いだろう。初めの2文字は 50×50 で2500パターンある。
計算は上の式の50の部分を2500にすれば良い。
答え:
60回ページをめくれば50%の確率で見つかる。
140回で98%見つかる。
2500パターンもあるのに?という感じだ、そりゃ誕生日攻撃流行るわ。
ではさらに、
問題:
初めの3文字が一致するページの組を探すならどうなる。初めの3文字は50×50×50で125000パターンある。
もう電卓を使っても計算するのが嫌だろう。
答え:
417回で50%を超える。
1000回なら98%だ。
人間が手動で探しているならこの辺でかなり厳しいが、コンピュータにやらせているのだ、これでもすぐに発見されてしまうだろう。秘密鍵は大丈夫なのか。大丈夫である。なにしろ実際は125000パターンどころではない、2の256乗パターンあるのだ。
文字のパターンが2の256乗になるように問題を書き直すとこうなる。
問題:
初めの45文字が一致するページの組を見つけるためには、何回ページをめくれば良いか。45文字は50の45乗 ≒ 2の256乗パターンある。だいたい 256 bit のハッシュ関数と同じだ。
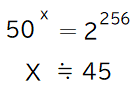
指数方程式(数Ⅱ)
試しに適当に机に積んである本をめくってみよう。

京極夏彦ー塗仏の宴ー
「つまりおよそこうとうむけいなりゆうきなのたかそれたけにわたいせいはあるものとみえてさいきん」
ひらがなにして50音の範囲に丸めているが、これで45文字だ。こういうことを何ページやれば同じ45字で始まるページの組が見つけられるかということだ。
いやいやいやいや無理でしょ、と思っただろうか。そう、無理なのである。これが誕生日攻撃に耐え得る256 bit ハッシュ関数の強衝突耐性なのだ。
計算すると、同じ45字で始まるページの組が50%の確率で見つかる試行回数は、
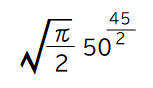
で、2.11 ×10の38乗 回となる。
これだけの回数ページをめくりまくって見つかるか見つからないか半々だ、これはもう無理だと言って良いだろう。
実際の256 bit ハッシュ関数の方も計算しておこう、
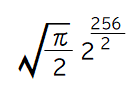
となるので、4.26×10の38乗 回の試行で同じハッシュ値を出す組が見つかる。
4.26×10の38乗 = 426澗 回だ、澗というのは億、兆、京、垓、秭、穰、溝、澗だ。
そして、これは強衝突耐性の話だ、自分の持っている秘密鍵をハッカーが特定するのは弱衝突耐性の話になるので、上で書いた通り、これよりも遥かに多い試行回数が必要となる。これはもう無理だと思わざるを得ないのではないだろうか。
自分の秘密鍵がたまたまハッカーの作った乱数と一致する可能性を考える場合、部屋の本棚を見て欲しい、そこから適当に本を取り出してページをめくり始めの45文字をメモしよう、次に同じ本でも別の本でも適当に開いて、そのページの初めの45文字がたまたまさっきメモしたものと同じである確率を考えてみる。
こんなものたまたまだろうが必死に探し回ろうが見つかる訳がない、というのが現在の話だが、近い未来では量子コンピュータがこれを見つけられるようになるらしい。
如何でしょうか、僕もこれを書き始める前は、たまたま何となくで被っちゃうことあるんじゃないの、無いとは言い切れないでしょ、と思っていたのだが、今は、無い無い、それは無い、と意見を変えている。僕の皮膚感覚ではなかなか良い例え話が作れたと思っているのだが、katakotoさんはどうだろうか、皆さんはどうだろうか。
意味わかんねーー、と言われたらどうしようか。
参考:
せっかくなので何回で50%を超えるかを Python に計算させてみた。
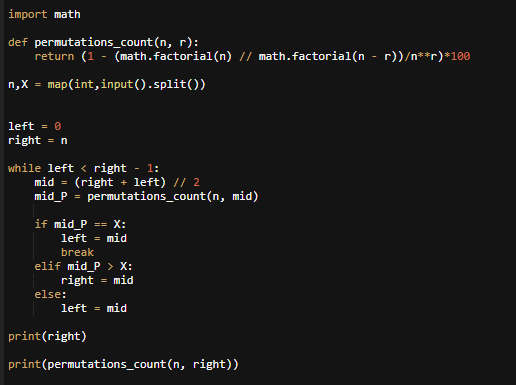
for文で回して探さずに二分探索を使っているところが勉強の成果だ。未だに何も作れないが着実にアルゴリズムには強くなっていっている気がする。
しかしこれでも125000パターンあると Python では通らなかった、PyPy でギリギリだ、AtCoder の PyPy を借りてしまったので自分の環境で PyPy も使えるようにしておかないと。
なんだろう、終わってみれば大学のレポートみたいになった、なんかすんません。
投稿者の人気記事




Bitcoin史 〜0.00076ドルから6万ドルへの歩み〜

梅雨の京都八瀬・瑠璃光院はしっとり濃い新緑の世界

京都のきーひん、神戸のこーへん

ジョークコインとして出発したDogecoin(ドージコイン)の誕生から現在まで。注目される非証券性🐶

無料案内所という職業

わら人形を釘で打ち呪う 丑の刻参りは今も存在するのか? 京都最恐の貴船神社奥宮を調べた

警察官が一人で戦ったらどのくらいの強さなの?『柔道編』 【元警察官が本音で回答】

警察官が一人で戦ったらどのくらいの強さなの?『柔道編』 【元警察官が本音で回答】

Bitcoinの価値の源泉は、PoWによる電気代ではなくて"競争原理"だった。

NFT解体新書・デジタルデータをNFTで販売するときのすべて【実証実験・共有レポート】

機械学習を体験してみよう!(難易度低)
