【Uniswap v3】集中流動性 (2)

シリーズでお送りしています。(1)はこちら。

前の記事で解説したのは、価格レンジ[Pmin, Pmax]を指定すると、sqrt(Pmax*Pmin)を中心価格とした集中流動性が実現されるということでした。

ところで集中流動性提供を始めるときの価格が中心価格ではなかったらどうなるでしょう?色々非対称になりますよね。アセット比重やImpermanent lossを見ていきましょう。

アセット比重

中心価格以外で流動性提供を始める様子を図にしてみました。

パラメータの定義は以下の通りです:

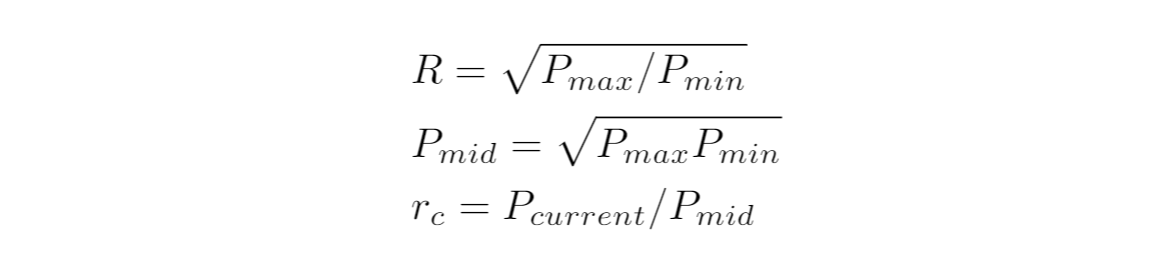
色々Pmidで規格化して考えると楽になります。

バーチャルプールではオレンジ点線とグリーン点線が正しい比率ですが、リアルプールではそれがオレンジ実線とグリーン実線になっています。グリーン実線の短くなっている様子がバーチャルプールよりも極端ですよね。

それぞれの線の長さを考えれば、リアルプールの在庫量は以下のように表せます:

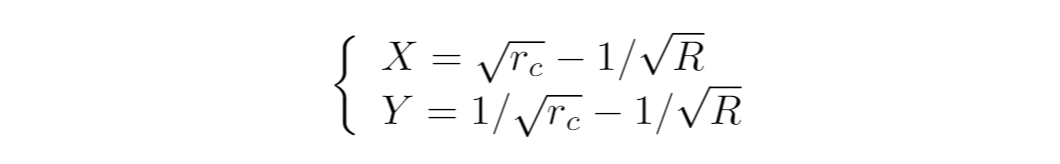
比重はこれらをもとに以下のようになります(Yには"価格"をかけることに注意):

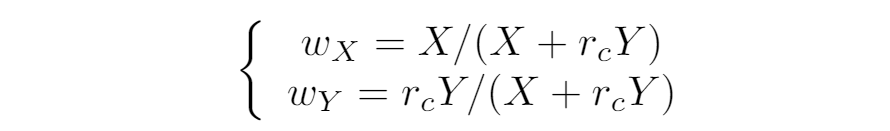
Impermanent loss

任意の価格におけるリアルプールの在庫量を定式化できたので、入場時価格(Pin)と退場時価格(Pout)を使ってImpermanent lossを計算することができます。

PinとPoutはPmidで規格化しておきます:

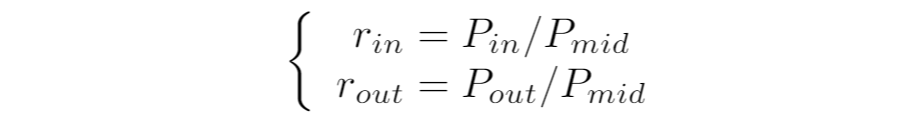
退場時のリアルプールの価値

退場時のリアルプール価値(Vout)をXの量で表すには、Yに価格をかけてXと足せばよいです:

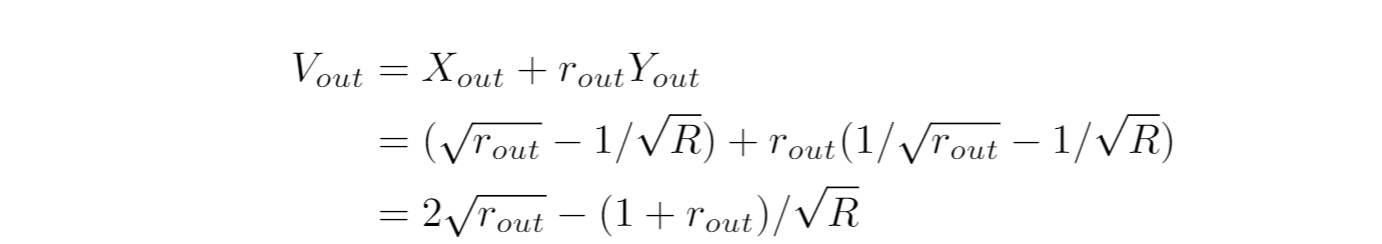
HODLしていた場合の価値

HODLしていた場合の価値(Vhodl)は、入場時のXの量と入場時のYの量と退場時の価格で表せます:

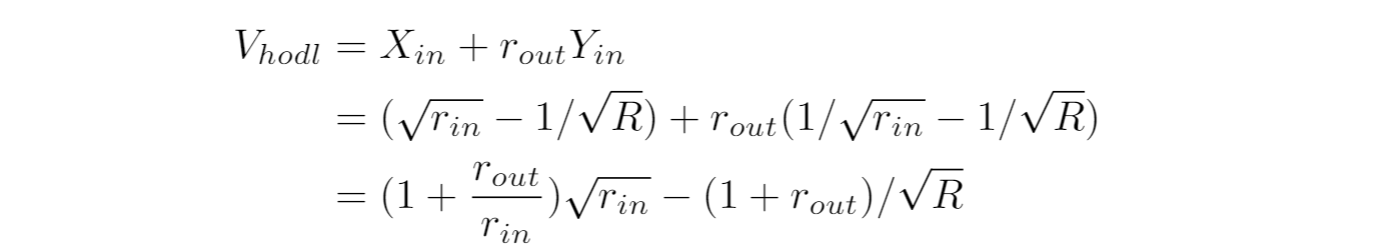
ということで、Impermanent lossは次のようになります:

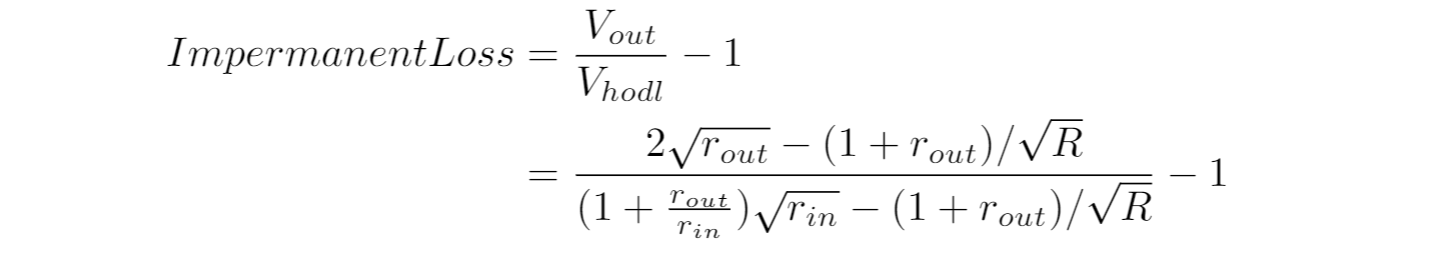
r_{out}/r_{in} = rが慣れ親しんだ価格変動率です。あえて分けて書いてみました。

ここまではPmidを基準に考えてみましたが、Pinを基準にパラメータを置き換えることもできます:

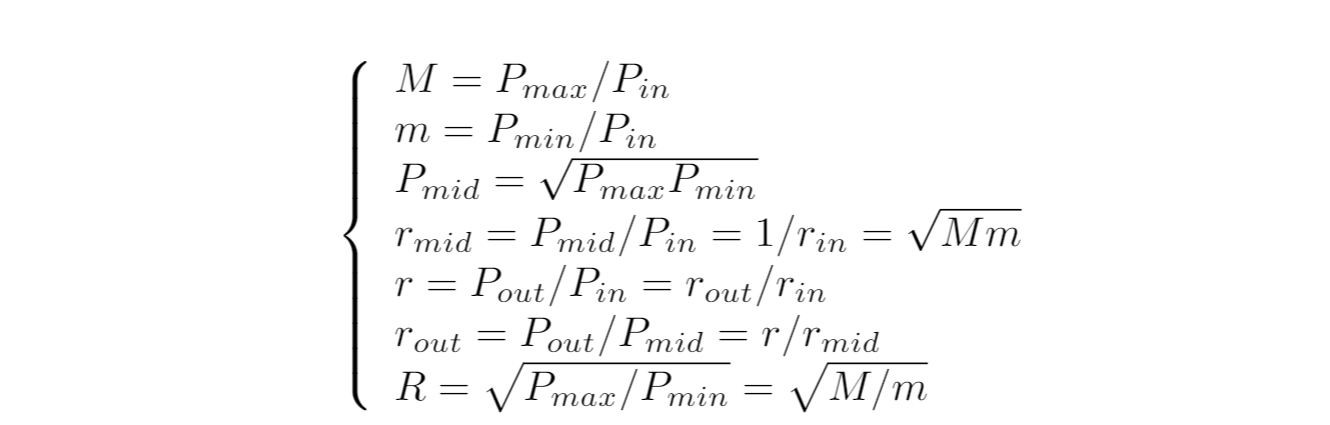
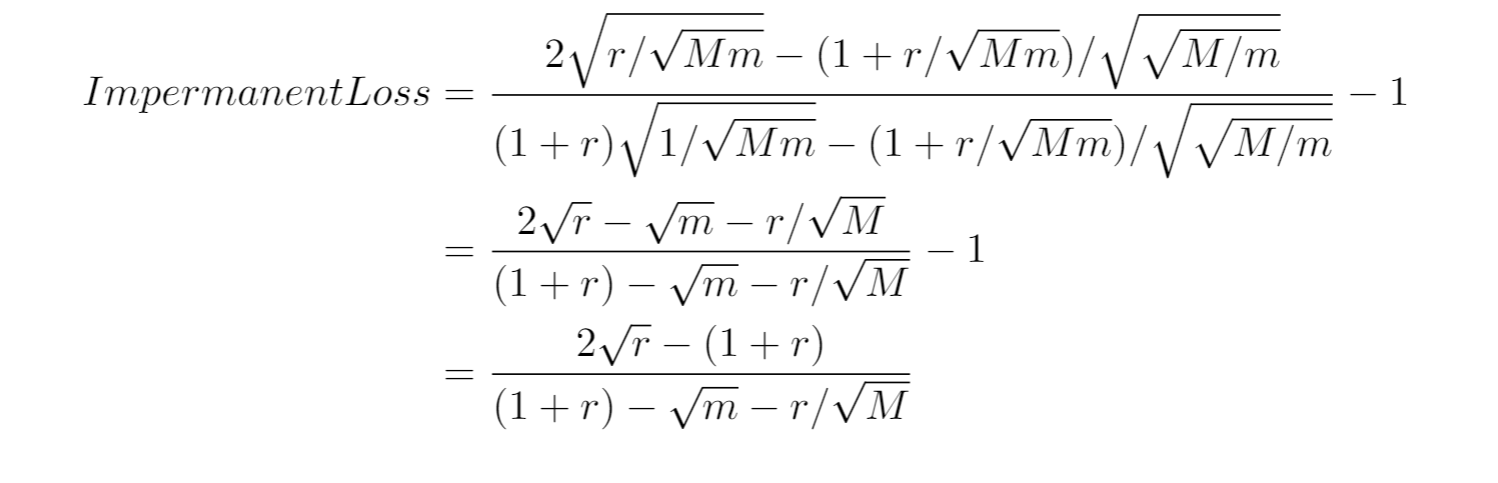
こちらの記事の7-3-3の場合に一致します。

さて、導出した式を使って、いくつかの場合を見てみましょう。

中心価格で入場する場合

以下のような条件です:

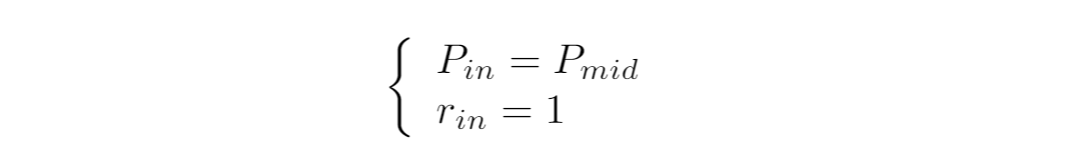
つまり、現在の価格を中心に1/RからR倍の範囲で集中流動性提供をしようという場合です。先の式に代入してみましょう:

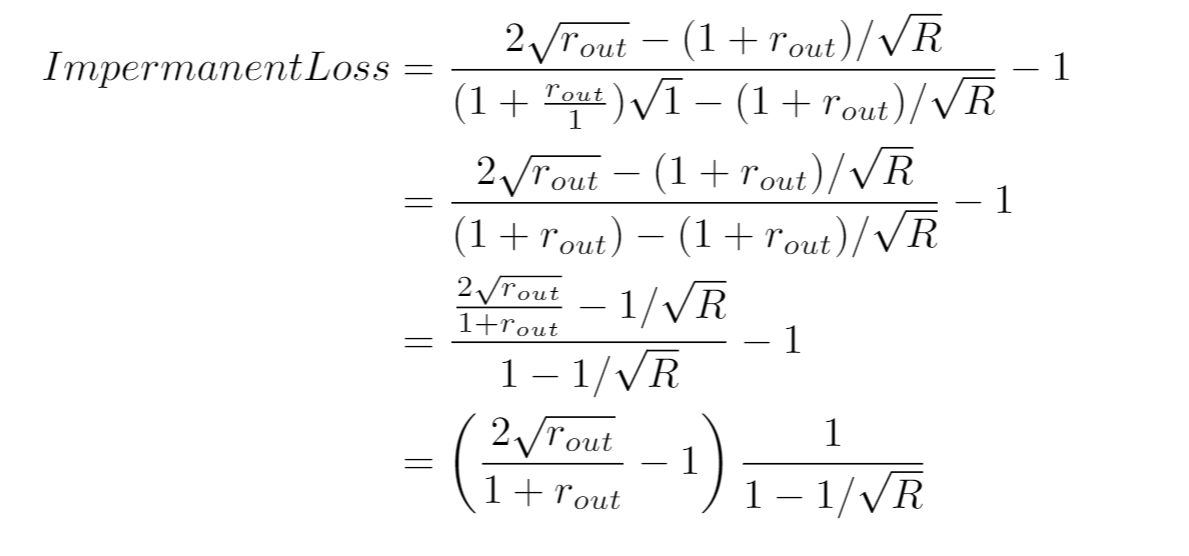
通常の範囲指定のない場合のImpermanent lossを、前回の記事で紹介した集中度倍した形になりました。

片面流動性提供

Pmin(あるいはPmax)から流動性提供を始める場合は"片面流動性提供"になります。パラメータの条件にすると以下の通りです:

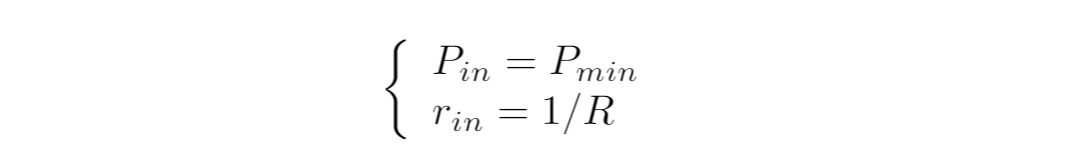
Impermanent lossは次のようになりますが、どのあたりまで整理すれば良いか迷っています:

レンジリミットオーダー

上記で退場価格がPmaxなら、それはレンジリミットオーダーです:

Impermanent lossと呼ぶのはもはや不適かもしれません:

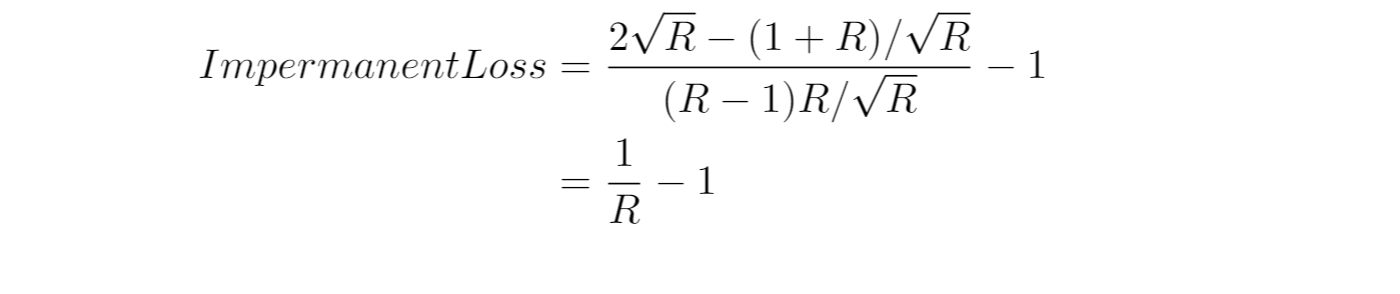
検討ポイント:集中度を取るか、損失を減らすか

片面流動性提供で検討項目になりそうなことを考えてみましょう。例えば今ETH価格が$1000であるとして価格$4000まで流動性提供するときに次の2通りを考えてみましょう:

- 端から中心: [$1000, $16000]の集中流動性提供をして$4000で退場する

- 端から端: [$1000, $4000]の集中流動性提供をして$4000で退場する

(端から中心の場合)

退場価格が中心価格なのでr_{out}=1と思えば良いです。

R=4、 集中度=2、 Impermanent loss=-33%。

(端から端の場合)

実質レンジリミットオーダーです。

R=2、集中度=3.4、Impermanent loss=-50%。

集中度の比は3.4/2=1.7

Impermanent lossの比は50/33=1.5

です。集中度を上げるとImpermanent lossが増えるのは確かですが、それは集中度の比率ほどは増幅されないことが分かりました。つまり、端から中心で途中退場しようというときに手数料がImpermanent lossを上回っている状況なら、(後からの結果論で)その価格をレンジ上限に設定できていたほうがもっと手数料を稼げていた、ということです。すなわち、もともと手数料が上回る見込みで流動性提供をするのなら、上限価格は退場予定価格にしておきましょう、という自然な結論が得られます。ただし逆も然りで、手数料が上回らなかった場合の損失は大きくなります。

まとめ

集中流動性提供を行う際のアセット比重とImpermanent lossを価格レンジ、入場価格、退場価格を使って定式化しました。Impermanent lossについてはいくつかの特殊ケースを見てみました。その結果、現在価格を中心価格とする場合には、レンジ指定のない慣れ親しんだ流動性提供の場合のImpermanent lossが集中度倍されることが確認できました。また片面流動性提供の考察もしてみました。

本記事では中心価格を基準に、曲線を固定して仮想プール軸をずらす考え方で色々導出を行いました。Uniswap v3のwhitepaperでは軸を固定して仮想プール曲線を記述しています。それに則った各要素の導出は@iketalike_max さんの記事で行われています:

また、うどんさんが計算機を作られています:

著者: kyoronut