基本情報技術者試験のお勉強 ～n進数➁

さて、昨日に引き続きほぼ自分向けのアウトプットです。笑

3人も、「いいね」(？)をいただいたようで、ありがとうございます。

今日はPythonで簡単に10進数→n進数に変換をする方法と、n進数における符号の表し方・補数について書いていきたいと思います。

1．Pythonで10進数をn進数に変換する方法

え？昨日関数作っていたじゃん？って話ですが、実はPythonにはいとも簡単にn進数に変換可能なコードがあるのですwww

でも、まずは原理を理解しないとってことで学ぶために自分で昨日のコードを書いたんですね～。意外と「まじめ」ですね、飯田さん。

では、10進数から2進数・8進数・16進数への変換について、以下に表します。

1行で良いんですよね(笑)

実際に実行すると・・・

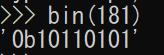
となります。昨日のコードで求めた結果と同じですね。

頭についている'0b'は2進数であることを示していて、2進数の英語「binary」の頭文字です。ちなみに、8進数は「octal」、16進数は「hexadecimal」です。

では、ついでにn進数から10進数に変換する方法も見ていきましょう。

10進数への変換は昨日も書いた通り、以下のように桁毎の重みを足し合わせる感じですね。

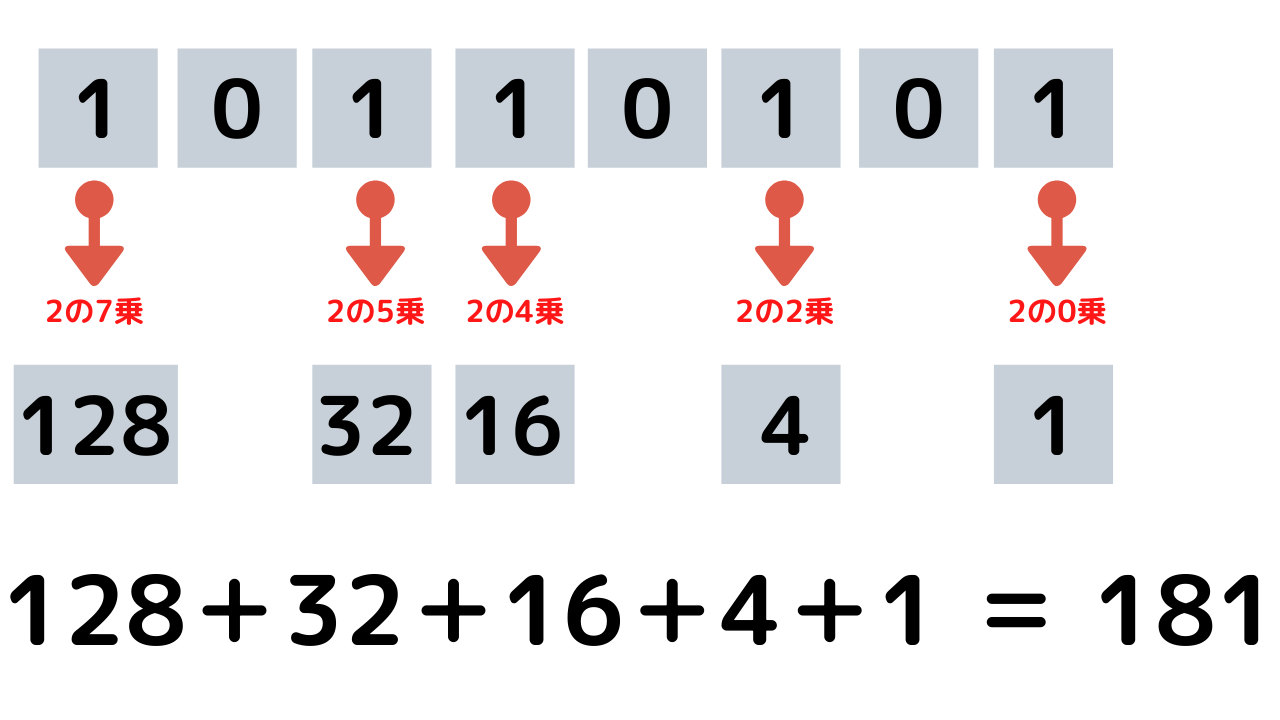
では、これをPythonで簡単に書くと・・・

たったこれだけです。

では、16進数で実験してみると・・・

大丈夫ですね。

では、次に再びPythonのコードを離れて、正負の数をn進数で表す方法について見ていきましょう。

2．n進数で正負を表す方法

10進数に符号をつける場合は、+181や－181といったように、先頭に「＋」か「－」をつけて表しますよね。

しかし、コンピューター内の計算において「＋」や「－」は利用できません。

そこで、符号ビットといい、符号を表す桁を１つ使うのです。

プラスの場合は「0」、マイナスの場合は「1」でこれを表します。

前回ご説明した通り、例えば1バイト(8ビット)で数字を表す場合、左端の1ビットを「符号ビット」にして、残りの7ビットで数字を表します。

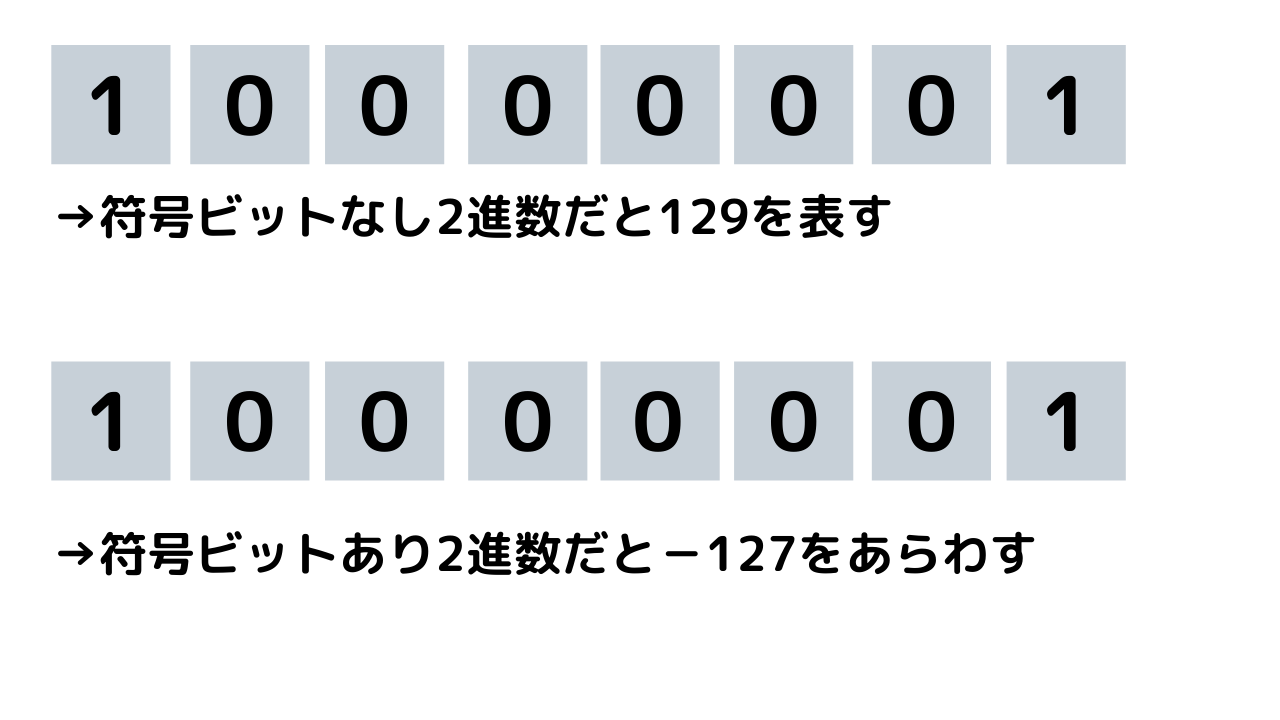
ふーん、くらいに思った方はそのままでもいいですが、ちょっとこんがらがってしまいますよね。疑問としては、何故同じ2進数なのに「符号あり」か「符号なし」で表す数が違うのか？コンピューターはどのように、「符号あり」か「符号なし」を見分けるのか？？？

まず、8ビット中の1桁を符号に使ってしまっているので、「符号あり」の場合、当然表せる範囲が変わってきます。

「符号なし」の場合、8ビットで0～255を表せますが、「符号あり」の場合、数字部分は7ビットとなるため、‐128～127までの256個しか表せなくなります。

次に、負の2進数については、マイナスを使わずに引き算を行うために「2の補数」のが必要となってきます。

3．2の補数とは？

補数についてちゃんと書くとめちゃくちゃ長くなってしまうので、2の補数が必要となる理由についてポイントを絞ってしっかり書こうと思います。

まず、補数とは何かですが・・・

補数（ほすう、complement）とは、ある基数法において、ある自然数 a に足したとき桁が1つ上がる（桁が1つ増える）数のうち最も小さい数をいう。応用の一例としては、計算機械において、「ある数から、xを引く」という操作を、加算する機械（加算器）で「ある数にxの補数を足す（ただし最も上の桁からの繰り上がりを無視する）」という操作でおこなうことができる、というものがある。

『ウィキペディア（Wikipedia）補数より』

じゃあ基数法って何？？？とかなっちゃいますよね(笑)

簡単に言うと、ある数に足したときに桁が1つ上がる最小の数が補数です。

例えば、10進数で考えた場合に桁があがる最小は10のべき乗です。

以下に何個か例を挙げてみます。

まだここまででピンと来た人もいるかもしれません。

実は補数というのは、「引き算」を「足し算」で表すことができるようになるのです。まずは分かりやすく、10進数を使って、800‐567を考えてみましょう。

結論から言うと、2の補数に符号ビット「1」を付けたものが負の2進数となります。

では2進数の計算を見てましょう。

どうでしょうか？　引き算を足し算で表現するために、2の補数を使ってコンピューター上では計算しているということを理解しました。（私が）

浮動小数点についても、書こうと思ってましたが、ちょっと疲れてしまったので（笑）、それは次回にします。