順列と組み合わせ

nonstop-iida
2020/03/05 10:02

さあ、お待ちかねの基本情報技術者試験のお勉強の時間です。(というより、自分の知識定着のためのアウトプット)

1．場合の数

順列や組み合わせに入る前に、まずは場合の数について書きます。～した場合に、何通りのパターンがあるか？これが場合の数です。

(1) 積の法則

2つの事象A・Bがある場合に、Aがx通り、Bがy通りである場合、場合の数は「x×y通り」となります。

例えば、トランプ(ジョーカー抜き)から2枚引いた場合の組み合わせは何通りか？

とすると、1枚目を引く時は52枚が選ばれる可能性があります。しかし、2枚目を引く時は1枚目を覗いた51枚が選ばれる可能性があります。トランプはマーク毎に13個の数字があり、かぶることはないため、52×51通り(2,652通り)が場合の数となります。

(2) 和の法則

次に事象Cとして、トランプから1枚も引かないという選択肢が有り得たとします。事象C単体の場合の数は1通りですが、事象A・B・C全体で見た時には、2,652通り＋1通り＝2,653通りです。

これは、事象A(1枚引く)・事象B(もう一枚引く)に対して、事象C(一枚も引かない)事は同時に起こり得ないからです。

なので2枚引く場合は、2,652通りあるが引かない1通りもあるので、場合の数としては2,653通りとなるわけです。

2．順列

(1) 順列の考え方

順列は、先ほどのトランプのように全体から何個かを順番に場合の数を求めるものです。順番に選んでいくので、1枚目・2枚目と選べる母数が減っていきます。このように選定場面が区別されるものは順列としてとらえます。(重複を排除しなくていい）

反対に2枚選ぶだけの場合、例えば♦のAと♠のAを選ぶのと、♠のAと♦のAを選ぶのは、結果として同一であるため組み合わせとしてとらえます。(重複を排除する必要あり）

例えば1枚目に♡のA・2枚目に♧のJを選んだ場合と、1枚目に♧のJ・2枚目に♡のAを選んだ場合、組み合わせでは重複としてカウントしませんが、順列ではカウントします。

1度選んだものは再度選べないことから、以下の通りとなります。

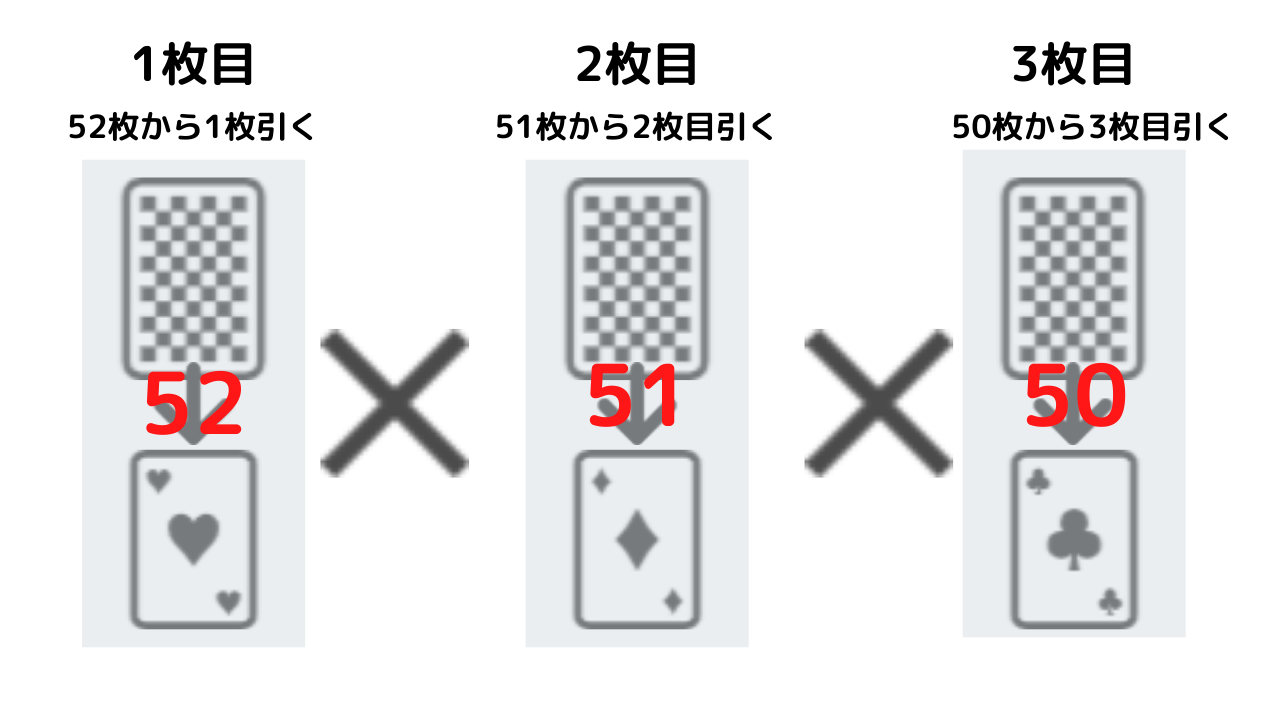
(2) 公式

公式ではnPr = n × (n-1)×(n-2)・・・×(n-r+1)となります。

(トランプの例の場合、52×(52－1)×(52‐3＋1)ですね）

(3) Pythonで順列を求める

Pythonで順列を求める計算をしてみましょう。順列を求める場合は、イテレータ生成ツールitertoolsを使います。

import itertools

card = []
mark = {1:'♥',2:'♦',3:'♧',4:'♠'}
numbers = [n for n in range(1,14)]

for i, m in mark.items():
   for num in numbers:
       card.append(str(m) + str(num))

permutations_  = set(itertools.permutations(card, 3))

print(len(permutations_)) #132600

for p in permutations_:
   print(p)

＜大まかな解説＞

➀ cardという空のリストを作成し、トランプのマークを格納したmarkという辞書と、1～13までの数字を格納したnumbersリストを用意して、2重ループで52枚のトランプカードを作成。

➁ 集合を作るsetを使い、itertools.permutations()の引数にcardリストと3枚選ぶので3を設定する。ちなみに、permutationsは英語で順列のことです。

print(len(permutations))で要素数を出力すると、132,600となります。(52×51×50)

更にforループで組み合わせを出力していますが、132,600通りなので、大変なことになります。飽きたら、ctrl + cでプログラムを止めてください(笑)

こんな感じになります(笑)

※ itertoolsについてのドキュメント

3．組み合わせ

次に組み合わせです。

(1) 考え方

先ほど、順列の説明で書いたように、全体から特に順番等を決めずに選ぶだけの場合、組み合わせが重複する可能性があり、これは排除する必要があります。

例えば、先ほどのトランプの例でいうと、順番を考えずに3枚選んだ場合の組み合わせは何通りでしょうか？という問題になりますね。

この場合、以下図の通りカードの並びを考慮しないので、発声する重複分を排除する必要があるんですね。

上の図のとおり、3枚の組み合わせには6パターンが存在するわけです。つまり、選べる全てのパターン(これは順列ですね）を、この重複パターンで割ると、重複を排除した組合せが出てくるわけです。

トランプだと数が大きすぎてイメージがわかないと思うので、1～5までの数字カードから3枚選んだ場合を考えてみましょう。

総数(順列)は5×4×3で6０通りですね。これを6パターンで割ると・・・

10通りとなります。

1始まりのパターンが・・・

{1・2・3} {1・2・4} {1・2・5} {1・3・4} {1・3・5} {1・4・5} 6パターン

2始まりのパターンが・・・

{2・3・4} {2・3・5} {2・4・5} 3パターン

3始まりのパターンが・・・

{3・4・5} 1パターン

これ以外のパターンは全て並び順が違うだけの重複なので10通りですね。

(2) 公式

組み合わせの公式はnCr = nPr/r! = n!/r!(n-r)! です。

!がついているのは階乗(5×4×3×2×1と階段状に乗算するもの)です。

nPr/r!はまさに60/3×2×1と、上でやった解き方です。

n!/r!(n-r)!が個人的には理解し辛かったのですが、nのr個目以下の階乗をさせる分、

分母に(n-r)!を加えたと考えたら理解できました。

(間違ってたらご指摘くださいm(_ _)m)

(3) Pythonで組み合わせを求める

順列で利用したitertoolsで組み合わせも対応可能です。

なんと、permutationsのところを、combinationsに書き換えるだけでOKです。(combinationsは組合せという意味です)

import itertools
card = []
mark = {1:'♥',2:'♦',3:'♧',4:'♠'}
numbers = [n for n in range(1,14)]

for i, m in mark.items():
   for num in numbers:
       card.append(str(m) + str(num))

permutations_  = set(itertools.combinations(card, 3))

print(len(permutations_))

for p in permutations_:
   print(p)

実行してみると・・・

22,100通りとなりました。

公式にあてはめると・・・52C3 = 52×51×50・・・・1×1 ÷ 3×2×1(49×48…×1)となります。

重複するところを端折ると、132,000÷6で22,100ですね。

4．最後に

おまけです。順列の場合に、仮に同じカードを複数回選んでよいという条件が加わったらどうでしょうか？

これを重複順列と言いますが、実はこれもitertoolsで対応可能です。productという処理が可能です。

import itertools
card = []
mark = {1:'♥',2:'♦',3:'♧',4:'♠'}
numbers = [n for n in range(1,14)]

for i, m in mark.items():
   for num in numbers:
       card.append(str(m) + str(num))

permutations_  = set(itertools.product(card, card, card))

print(len(permutations_))

for p in permutations_:
   print(p)