🍎グラフ理論のすすめ３🍎

sphiarno-88
2022/01/19 13:09

🍌はじめに

最近、私はCOBOLのプログラミング学習をしています。というのも、近年の金融機関などのトラブルから、そこのメインフレームで使われているCOBOLというのはどういう言語なのか、ということと、Fortranと同様な古代兵器？が現代の環境にどうのような影響をあたえるのか、ということが気になったからです。

ちなみにFortranについては、今でこそ例えば「Python！Python!」と言われてますが、それを支える基幹パッケージであるNumPyやSciPyは、実質のC++またはFortranであり、したがってそれらを利用するPandas、SkLearnなど、機械学習やデータサイエンスを支えるフレームワークにおいてもなお、Fortranは無視できない存在になっています。

Termuxで利用していたPythonのSklearnは、おそらくRool化不要のためにFortranの変形して使用できるようにされていたもので、自分でFortranやSklearnをビルドできるならば直接リポジトリから利用できるのでしょうが、そのような知識もなく、またTermuxがローリング環境であるために、Pythonが早早に3.10に移行した関係で参照不能になり、利用できなくなりました。

またCOBOLについては、現在においても世界で動作している言語のランキングに入る、と影響力が大きい状況もあるようです。なんでも昔あった2000年問題は、この言語の「ACCEPT データ項目 FROM DATE」による方法が、YYMMDDというフォーマットを持っていたことに起因するようです。

しかし、よく言われているように、COBOL自体はそもそも問題なのだろうか？BCD（バイト１０進数）以外のメリット、例えば速度などのメリットはあるのだろうか？疑問がわいてきます。そこで、言語のベンチマークとして、昨年懸賞金がついて話題になったコラッツ予想に関するページがあったので、自身へのCOBOLテストとしてやってみました。

コラッツ予想が、主としてではないものの、グラフ理論と関わりがあることは明白であるので、今回、グラフ理論の応用？として取り上げてみます。こちらはPythonですが、今回はベンチマークもかねたのでNetworkXは使用しませんでした。「やり方を忘れただけだろ」なんて言わないでね。

なお、こちらを参考にしました。

🍈学習中のCOBOLで

COBOLは高級言語（予約語や定形処理が多い）と言われてますが、やってみた感じは、環境宣言やデータ宣言が必要なあたり、むしろシステム的な感じがしました。CASLⅡ（アセンブラ）を以前やっていたからかもしれません。不思議なのは、なにか間違えているようでもぬるぬる動く、ということでしょうか。がちがちな環境定義に思えて、意外にゆるいのはかえって危険かもしれません。クラスの普段図書館にいてほどんど喋らないおとなしい子が、実は…みたいな、完全な偏見と希望的妄想ですが…

ちゃんとできているかは不明ですが、COBOLでのコラッツ予想です。使用したのはGNU-COBOLで、記述方式はフリーモードです。

IDENTIFICATION   DIVISION.
PROGRAM-ID.   COLLATZ.
ENVIRONMENT   DIVISION.
DATA    DIVISION.
WORKING-STORAGE   SECTION.
 01 WK-COL.
   03 WK-COL-N PIC 9(22) VALUE ZERO.
   03 WK-CIF PIC 9(1) VALUE ZERO.
   03 WK-CNT PIC 9(22) VALUE ZERO.
 01 WK-MAIN.
   03 WK-N PIC 9(22) VALUE ZERO.
   03 WK-I PIC 9(22) VALUE ZERO.
   03 WK-ANS PIC 9(22) VALUE ZERO.
 01 WK-FUGA.
   03 WK-HOGE PIC 9(22) VALUE ZERO.
PROCEDURE   DIVISION.
MAIN.
 DISPLAY "N?: " WITH NO ADVANCING.
 ACCEPT WK-N FROM CONSOLE.
 PERFORM VARYING WK-I FROM 1 BY 1
 UNTIL WK-I &gt; WK-N
&gt;&gt;D    DISPLAY "WK-COL-N: " WK-I
   COMPUTE WK-COL-N = WK-I
   MOVE ZERO TO WK-CNT
&gt;&gt;D    DISPLAY "WK-CNT: " WK-CNT
   PERFORM WITH TEST BEFORE UNTIL WK-COL-N = 1
     ADD 1 TO WK-CNT
     DIVIDE 2 INTO WK-COL-N GIVING WK-HOGE REMAINDER WK-CIF
     IF (WK-CIF = 0) THEN
       COMPUTE WK-COL-N = WK-HOGE
&gt;&gt;D        DISPLAY "WK-COL-N: " WK-COL-N
     ELSE
       COMPUTE WK-COL-N = WK-COL-N * 3
       COMPUTE WK-COL-N = WK-COL-N + 1
&gt;&gt;D        DISPLAY "WK-COL-N: " WK-COL-N
     END-IF
   END-PERFORM
&gt;&gt;D    DISPLAY WK-I ": " WK-CNT
   ADD WK-CNT TO WK-ANS
   DIVIDE 1000000007 INTO WK-ANS GIVING WK-HOGE REMAINDER WK-ANS
 END-PERFORM.
 DISPLAY WK-ANS.
 STOP RUN.
END PROGRAM COLLATZ.

ベンチマークの結果は、のちほど、のちほど。

🍓遅いのはPythonのせい？

参考先のコラッツ予想プログラムで言われていたのは、Pythonはビリクラスの速度の言語であった、ということです。確かに、直線的にただただ解を求めて行くようなアルゴリズムの場合には、基本的にすべてがオブジェクト型であるようなPythonでは不利な感じもします。しかし、コラッツ予想の場合にはグラフ構造があり、必要時にノードを参照し、今後参照すべき必要がなくなったら消す、という方法によれば、ガーベジコレクションを備えるPythonには、一定の有利面があるようにも思います。

１）

１と２と４はループになって都合が悪いので、ここの部分だけ調整して３から開始し、ノード（データ）生成および消滅させるように作ります。が、まずはテストです。ここでは期待どおりのノードが生成・消去できるかテストします。

データは辞書型にします。呼び出し番号をインデックスにし、（距離、（×３＋１からの呼び出しがあったか、自分自身からの呼び出しはあったか、÷２からの呼び出しはあったか））を納め、全て呼び出された場合にそのデータを消去（POPで取り出して再登録しない）します。入力、出力を多くしているのがポイントです。

collatz_dict ={
    4: (2, (True, False, bool(input("test no4 hi bool(Not None): ")))),
}
print(collatz_dict[4])

call_n = int(input("test call_no(4): "))
call_mt = (0, 1, 2)[int(input("test call_method 0:2(2): "))]  # =(lo, slf, hi)

result = collatz_dict.pop(call_n, False)
if result:
    (itr_n, (lo, slf, hi)) = result
    n_crt = 0
    n_del = 0
else:
    (itr_n, n_crt, n_del) = (10, 10, 10)  # dummy call function
    lo = (False, True)[0]  # dummy function
    slf = False
    hi = False
    itr_n = itr_n + 1
    n_crt = n_crt + 1

print(call_n, ":", itr_n, "(", lo, slf, hi, ")")
print("curent n_crt, n_del:", n_crt, n_del)

if (call_mt//2):
    hi = True
elif (call_mt//1):
    slf = True
else:
    lo = True

if hi and slf and lo:
    print(call_n, "is deleted.")
    n_del = n_del + 1
    # print(collatz_dict[call_n])  # &lt;&lt; error-check
else:
    collatz_dict[call_n] = (itr_n, (lo, slf, hi))
    print("renew", call_n, ":", collatz_dict[call_n])

print("return: ", itr_n, n_crt, n_del)

（実行例）

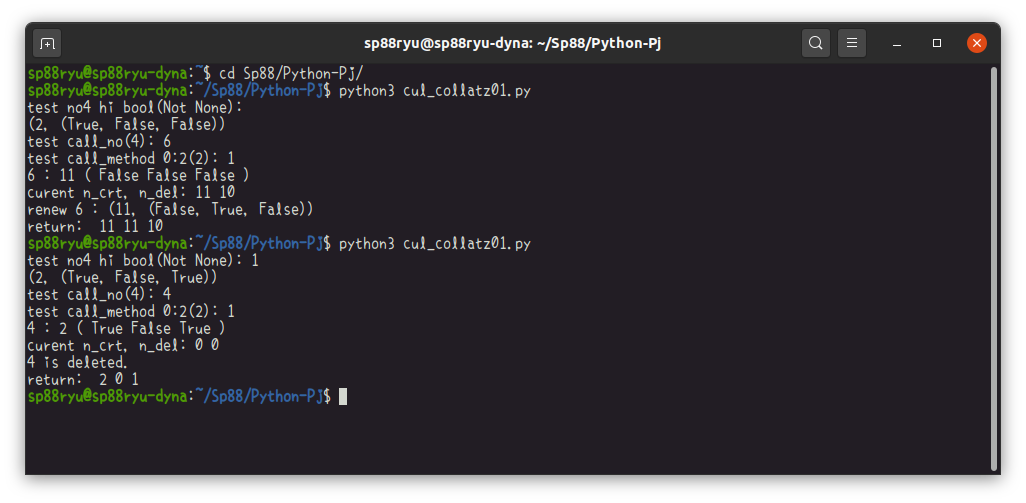
ダミーの辞書が登録できたこと、４が自身を参照して辞書を消去したことが確認できます。

２）

次に、テストを関数化します。こんどは３のコラッツ予想をしたとき、うまく関数が機能するか確認します。先程述べたように、１，２，４はループになっていろいろ都合が悪いので、１，２はすでに終わって、登録辞書にはなぜか４だけある状態｛４：（２、（True、False、False）｝を仮定させます。３は４を参照するはずなので、４の８からの参照（一番最後）がTrueになればOkでしょう。

def call_collatz(x: int, method: int) -&gt; (int, int, int):
   result = collatz_dict.pop(x, False)
   if result:
       (_itr_n, (_lo, _slf, _hi)) = result
       _n_crt = 0
       _n_del = 0
   else:
       # _call_n, _call_mt
       if not(x%2):
           _call_n = x // 2
           _call_mt = 2
       else:
           _call_n = x * 3 + 1
           _call_mt = 0
       (_itr_n, _n_crt, _n_del) = call_collatz(_call_n, _call_mt)
       _lo = bool((x-4)%6)
       _slf = False
       _hi = False
       _itr_n = _itr_n + 1
       _n_crt = _n_crt + 1

   print(x, ":", _itr_n, "(", _lo, _slf, _hi, ")")
   print("curent n_crt, n_del:", _n_crt, _n_del)

   if (method//2):
       _hi = True
   elif (method//1):
       _slf = True
   else:
       _lo = True

   if _hi and _slf and _lo:
       print(call_n, "is deleted.")
       _n_del = _n_del + 1
       # print(collatz_dict[x])  # &lt;&lt; error-check
   else:
       collatz_dict[x] = (_itr_n, (_lo, _slf, _hi))
       print("renew", x, ":", collatz_dict[x])

   print("return: ", _itr_n, _n_crt, _n_del)
   return (_itr_n, _n_crt, _n_del)


# --- test procedure ---
collatz_dict ={
   4: (2, (True, False, False)),  # del test
}
print(collatz_dict[4])

# ref
call_n = int(input("test call_no(3): "))
call_mt = (0, 1, 2)[int(input("test call_method 0:2(1): "))]  # =(lo, slf, hi)

result = collatz_dict.pop(call_n, False)
if result:
   (itr_n, (lo, slf, hi)) = result
   n_crt = 0
   n_del = 0
else:
   # call_n, call_mt
   if not(call_n%2):
       dm_call_n = call_n // 2
       dm_call_mt = 2
   else:
       dm_call_n = call_n * 3 + 1
       dm_call_mt = 0
   (itr_n, n_crt, n_del) = call_collatz(dm_call_n, dm_call_mt)
   #----
   lo = bool((call_n-4)%6)
   #----
   slf = False
   hi = False
   itr_n = itr_n + 1
   n_crt = n_crt + 1

print(call_n, ":", itr_n, "(", lo, slf, hi, ")")
print("curent n_crt, n_del:", n_crt, n_del)

if (call_mt//2):
   hi = True
elif (call_mt//1):
   slf = True
else:
   lo = True

if hi and slf and lo:
   print(call_n, "is deleted.")
   n_del = n_del + 1
   # print(collatz_dict[call_n])  # &lt;&lt; error-check
else:
   collatz_dict[call_n] = (itr_n, (lo, slf, hi))
   print("renew", call_n, ":", collatz_dict[call_n])

print("return: ", itr_n, n_crt, n_del)

（実行例）

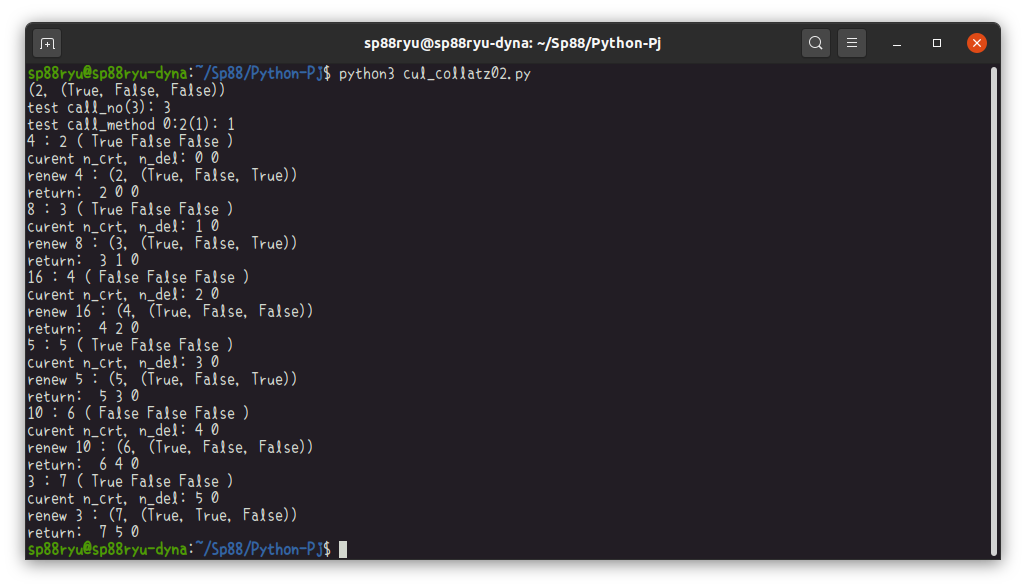
経路を出力しているので、小さい値を入力すれば確認できます。また、４にいった帰りで５つの要素を作成していることもわかります。

３）

最後にこれらをまとめます。最大値を入力して、コラッツ距離を３から最大値まで計算するようにします、なお返却値として（それまでの距離、作成したノードの合計、消去したノードの合計）を返します。そして、作成・消去のノード計を最大値の繰り返しまで合計し、最後に出力します。

# data difinition
collatz_dict = {
   4: (2, (True, False, False)),
}

def call_collatz(x: int, method: int) -&gt; (int, int, int):
   global collatz_dict
   result = collatz_dict.pop(x, False)
   if result:
       (_itr_n, (_lo, _slf, _hi)) = result
       _n_crt = 0
       _n_del = 0
   else:
       if not(x%2):
           _call_n = x // 2
           _call_mt = 2
       else:
           _call_n = x * 3 + 1
           _call_mt = 0
       (_itr_n, _n_crt, _n_del) = call_collatz(_call_n, _call_mt)
       _lo = bool((x-4)%6)
       _slf = False
       _hi = False
       _itr_n = _itr_n + 1
       _n_crt = _n_crt + 1

   # print(x, ":", _itr_n, "(", _lo, _slf, _hi, ")")
   # print("curent n_crt, n_del:", _n_crt, _n_del)

   if (method//2):
       _hi = True
   elif (method//1):
       _slf = True
   else:
       _lo = True

   if _hi and _slf and _lo:
       # print(x, "is deleted.")
       _n_del = _n_del + 1
   else:
       collatz_dict[x] = (_itr_n, (_lo, _slf, _hi))
       # print("renew", x, ":", collatz_dict[x])

   # print("return: ", _itr_n, _n_crt, _n_del)
   return (_itr_n, _n_crt, _n_del)

def main():
   statistics = []
   hash = 0
   sum_crt = 0
   sum_del = 0
   max = input("max: ")
   for i in range(3, int(max)+1):
       (_res, _crt, _del) = call_collatz(i, 1)
       # print(i, "(res, crt, del):", _res, _crt, _del)
       sum_crt += _crt
       sum_del += _del
   print("sum(crt, del):", sum_crt, sum_del)


if __name__ == '__main__':
   main()

（実行例）

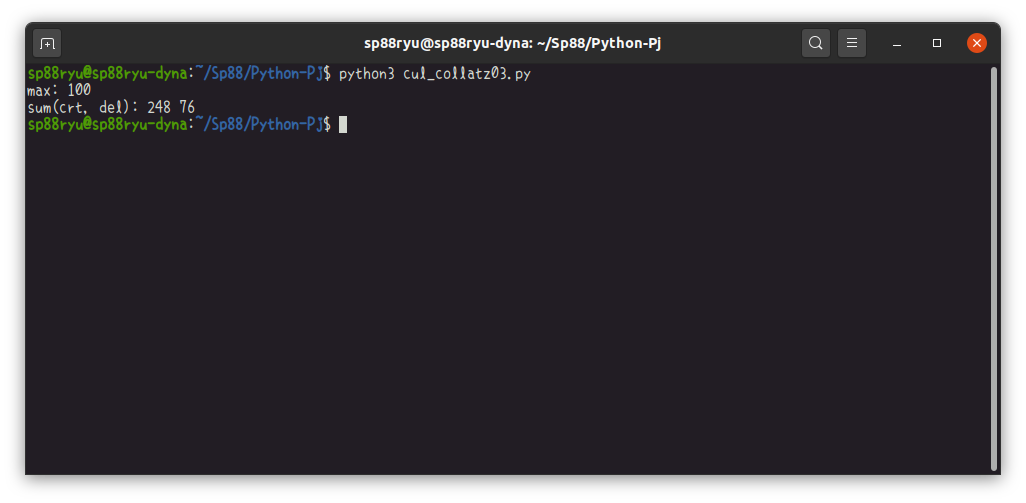
できました。へいへい！

🍇統計もとってみる

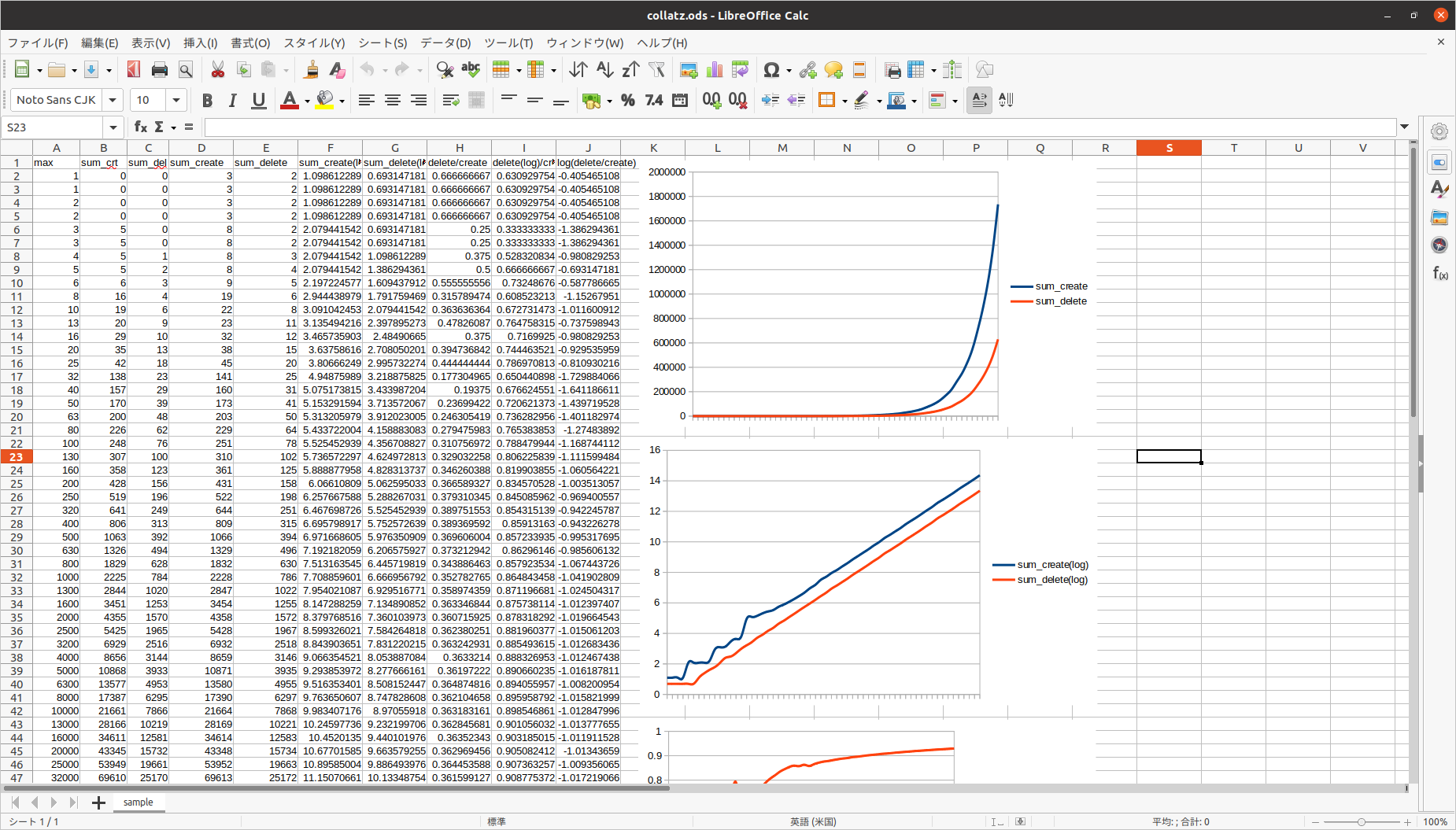
ここでベンチマークに行きたいところですが、お楽しみは最後にとっておいていただくとして、せっかくなので統計もとってみます。グラフ化したいので、まずPythonコードの入力をコマンドラインのargvからとるように変更します。

#python change section
import sys
#...
def main():
    #...
    max = sys.argv[1]
    #...
    print("%s, %s" % (sum_crt, sum_del))

#...

そして、BashからPython実行し、出力先をCSVファイルに追加するように変更します。その中で、指数リスト化された最大値を入力として繰り返すようにします。

#!/bin/bash

array=(
   1 1 2 2 3 3 4 5 6 8
   10 13 16 20 25 32 40 50 63 80
   100 130 160 200 250 320 400 500 630 800
   1000 1300 1600 2000 2500 3200 4000 5000 6300 8000
   10000 13000 16000 20000 25000 32000 40000 50000 63000 80000
   100000 130000 160000 200000 250000 320000 400000 500000 630000 800000
)

for e in ${array[@]}; do
   python3 collatz_args.py ${e} &gt;&gt; sample.csv
done

おや、どこかで見たことのある数列でしょうか。そんなあなたは「グライコ・マニア」ですね。

では、結果をグラフにしてみます。ただし、１と２を入力したときはプログラムが（０、０）をかえしてきて、これまた計算上都合が悪いので、１と２と４の辞書を作ったけど１と２の辞書はすでに消した、ということにして、作成数には３のバイアスを、消去数には２のバイアスを、全体にかけます。

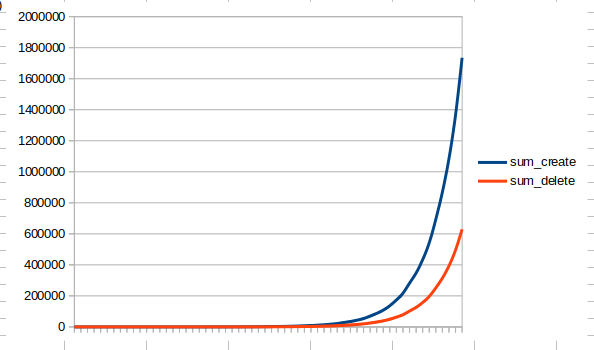
横軸を指数的にとっていることもありますが、これでは急増加しているだけで、なんのことかわかりません。縦軸も指数化してみましょう。自然対数に変更します。

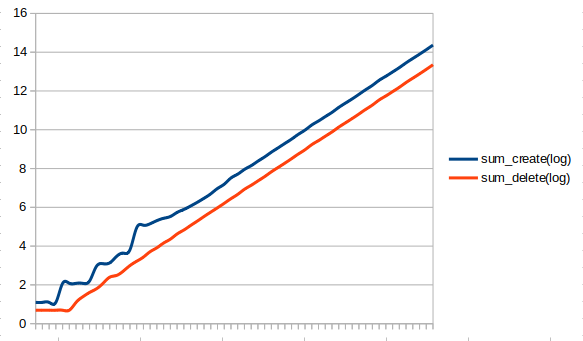
なんとも気持ちの悪いグラフが出てきました。普通そうなるのでしょうか？よくわかりませんが、平行線になってしまいました。まるで、君と僕の距離みたいな関係です。消去数を作成数で割ってみます。

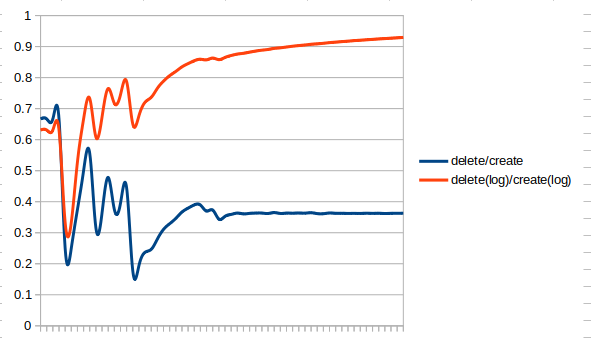
こちらも不気味なグラフになりました。それぞれのログから計算した赤いほうは、１に近づいているのでしょうか？また、それぞれの純粋な合計で計算した青い方については、一定値におちついているようにも見えます。しかも、なにか気持ちの悪い固定値です。そのログをとってみます。

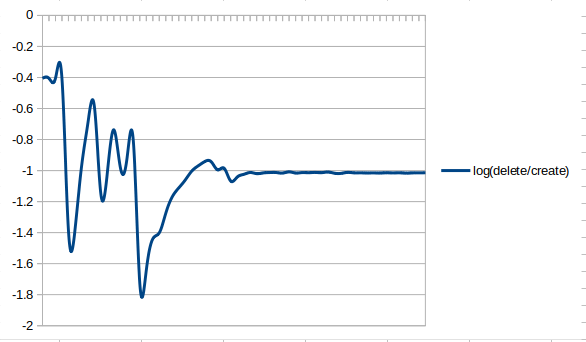
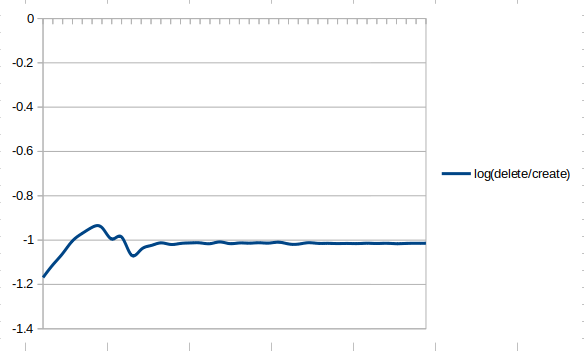
はい、でました。（消去合計÷作成合計）が、自然対数の超越数といわれるｅと、いかにも関係があるかのようなグラフです。ただの偶然でしょうか？それとも、そうなるように計算しただけの必然なのでしょうか？さらに気持ちの悪いのは、近づいているような縮まってないような、ー１よりわずかに低い値をキープしていることです。まだ計算余力はあるものの、試してみるには少々自分の頭のほうが能力不足であるようにも感じます。

「この解がそこに収束するならコラッツ予想は正しい」と言えるなら、少しは期待してもいいかもですが、そもそもこのグラフがなにを意味するかは、よくわかってません…言えることがあるとすれば、この方法で計算効率性はかせげたとしても、ガーベジコレクションがあったところで、いつかはメモリ効率面で限界を迎えるであろうということでしょう。

Goなどの並列系で、時間効率性と計算効率性を競合させるようなものを作れば、また面白いのかもですが…例えば、こんな感じです。

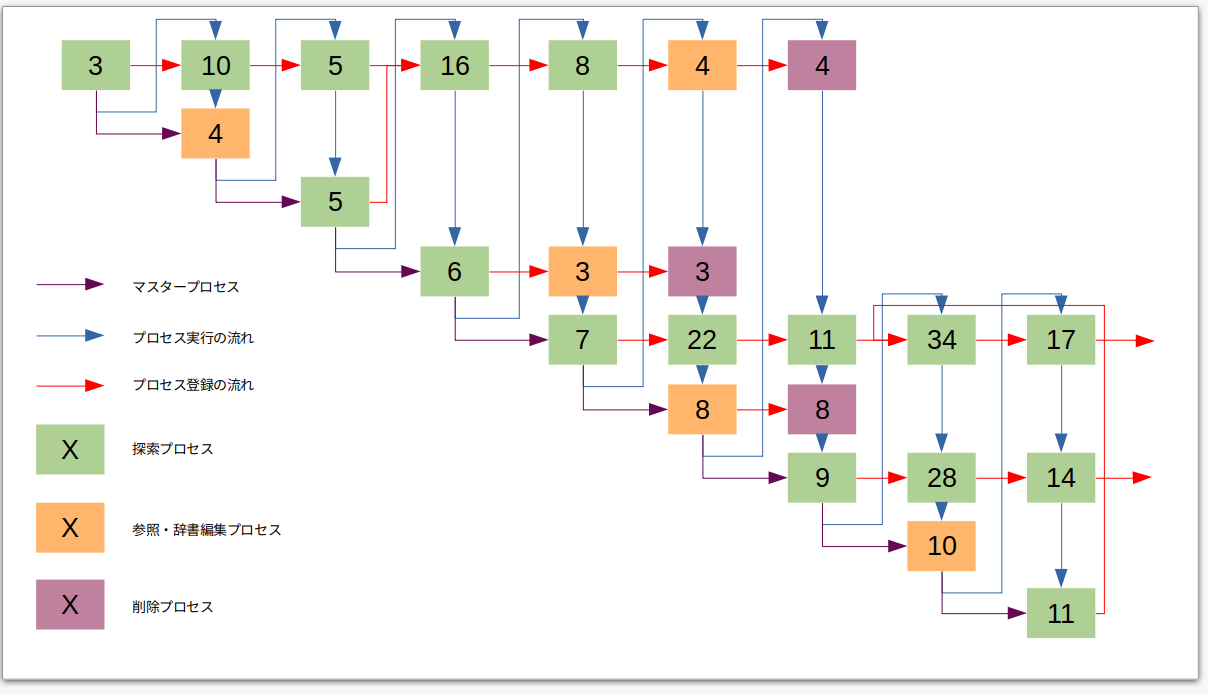
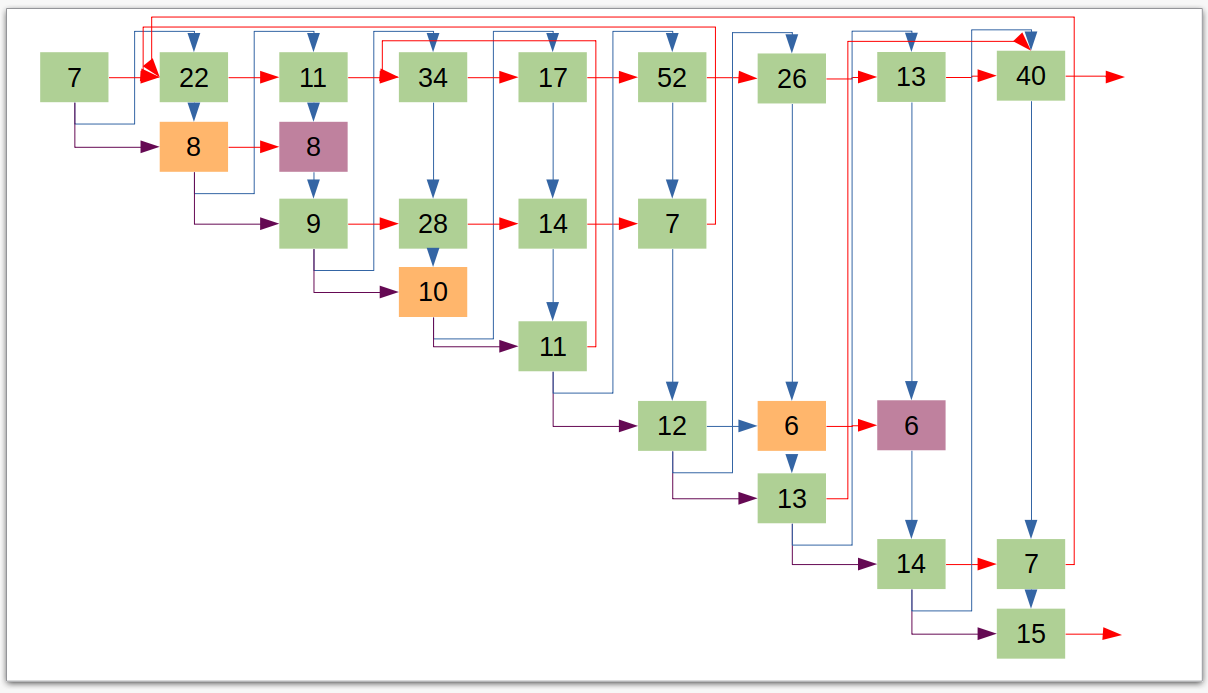
いっておいてなんなのですが、これでは今のところ美味しい感じはしません。工夫が必要そうですが、これはまた今度かなあ…

🎉結果発表

それでは結果発表です。

まずこの環境での能力がわかるように、Ｃ系で実行したときの結果です。

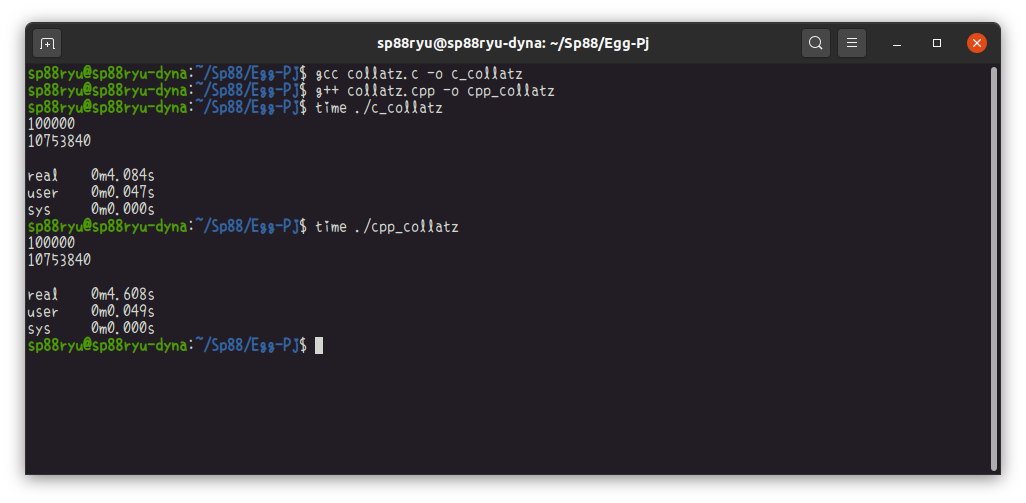
さすがＣです。コンパイラは怪物のLLVMではなくGCCです。が、とにかく速いです。あとで、他ものと比べるとよくわかります。

次はグラフ辞書？を利用しない場合のPythonです。

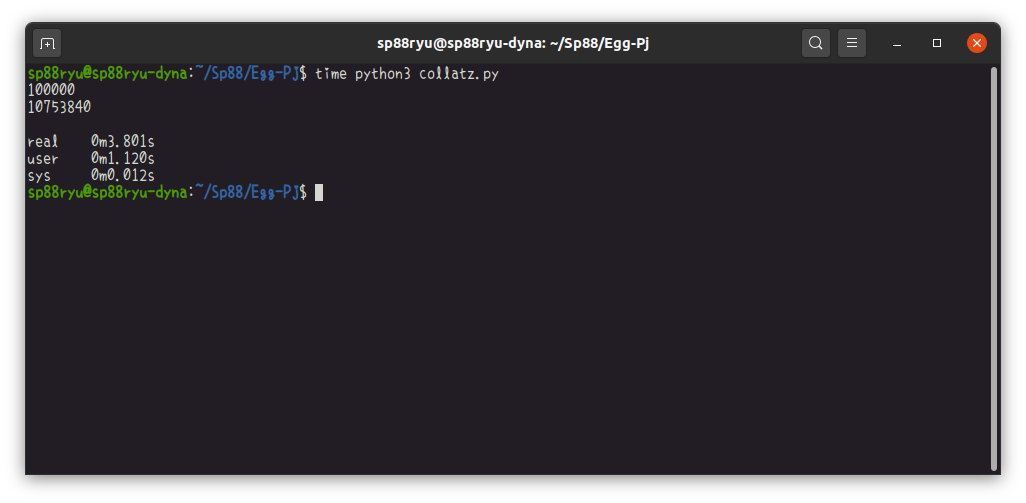
比較してＣより随分遅いです。が、最近のコンピュータはとにかく速いので、どうにも使えないというようなスピードではないように思います。

次はグラフ辞書を利用した場合のPythonです。グラフ理論というより、ある意味ただのカンニングです。

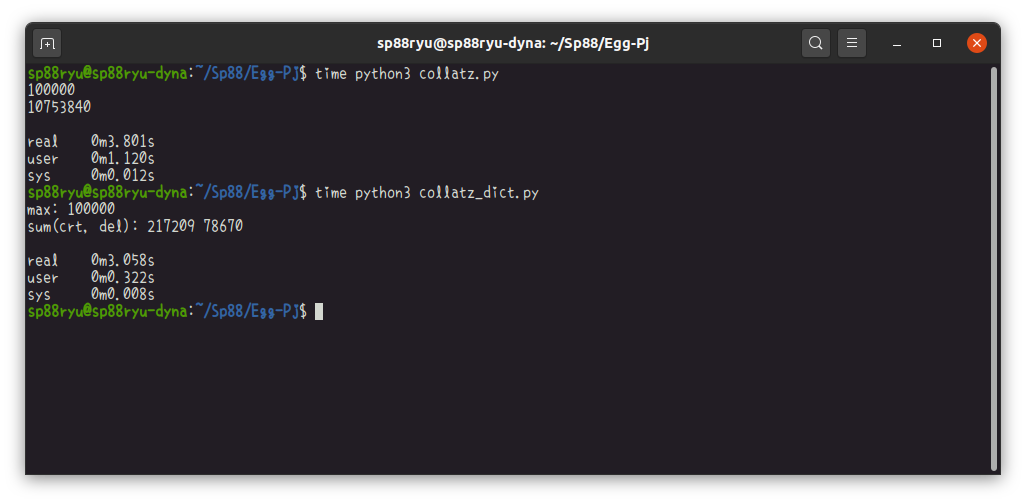
ズルをしているからかわかりませんが、ややこしいことをしている割には、何もしないPythonに比べて３倍くらい速くなりました。答え合わせのためのハッシュ計算はしてないですが、あってもなくても速度面ではほとんど差がありませんでしたので、考慮してません。アルゴリズムの勝利ですね、やったぜベイベー。

最後に、われらがクラッシャー、COBOLです。

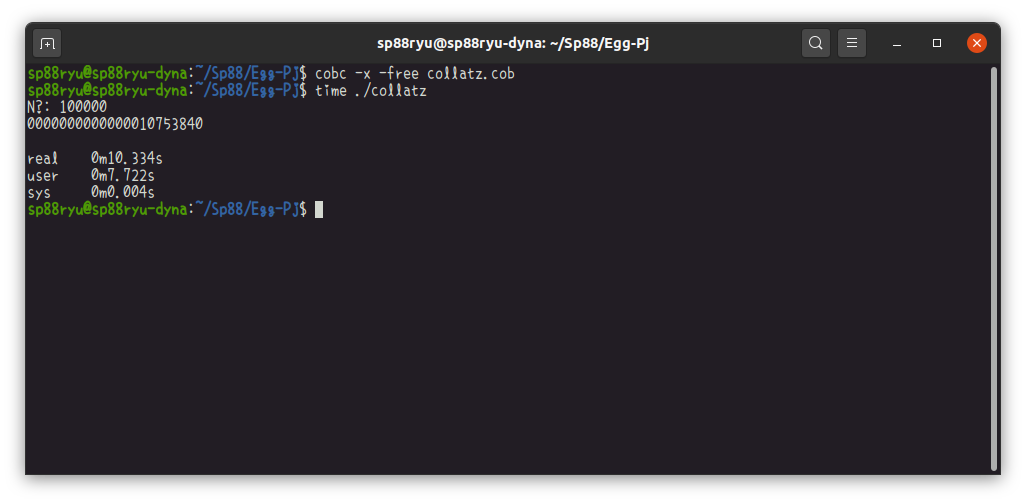
速度面では期待していたのですが…やり方が悪いのか「おい！」とツッコミたくなる結果です。２で割るというのと、バイト１０進数の相性が悪い（逆に他の言語で相性がいい）関係かもしれません。

⛵終わりに…

ということで、グラフ理論をコラッツ予想にかけあわせてコーディングして、ベンチマークしてみました。伝説の？プログラミング言語：COBOLの結果には残念でしたが、Pythonの統計・ベンチマークテストからはたいへん良い結果が得られたように思います。まあ、間違いはいろいろあるかもですが…

コラッツ予想の計算だけなら、アセンブラのシフト演算を利用した方法などもおもしろそうです。そして、これが実はコラッツ予想の決定的証明に…とかなって「懸賞金贈呈です」となってもおもしろいですが、自分の実力ならせいぜい、超越コボラーとなって全世界の金融システムを破壊し相対的金持ちになる、くらいが関の山でしょう。まあ、それさえ全然不可能ですが…なんて、ちゃんちゃん。

☕〜　おしまい　〜☕