🌀　螺旋の螺旋　🌀

（記事作成日：2020年6月18日）

◇　螺旋の連続をパイソンで作ってみようプロジェクト

螺旋の螺旋の…というものがどんなものか見たかったので、作ってみました。

螺旋上の螺旋上の…の螺旋というのは構成方法にもよりますが、無限次元の無限序数の位相空間を三次元内に表現することができます。

そう言うと、なにか凄いコンパクト性に思えてきますが、一次元内にも理論上は表現可能です。

（wikipediaより、チューリングマシン）

一次元上では想像するのにあまり面白みを感じなかったので、ネットで三次元の画像を探してたのですが見つかりませんでした。

いろいろモチベーションになるものもあり、ちょっと難しかったのですが頑張りました。ですが、間違いはあるかもです。

◇　螺旋の螺旋

まずは簡単なものからのチャレンジです。簡単とはいっても、平面空間のベクトル遷移を考えないといけないので意外に面倒です。

考え方としましては、

①XY平面で円を描くが、その半径が小さい三角関数で伸び縮みする。

②Z軸は大きくは一定速度で上昇するが、小さくは三角関数で上下する。

という感じでしょうか。

下のものができました。

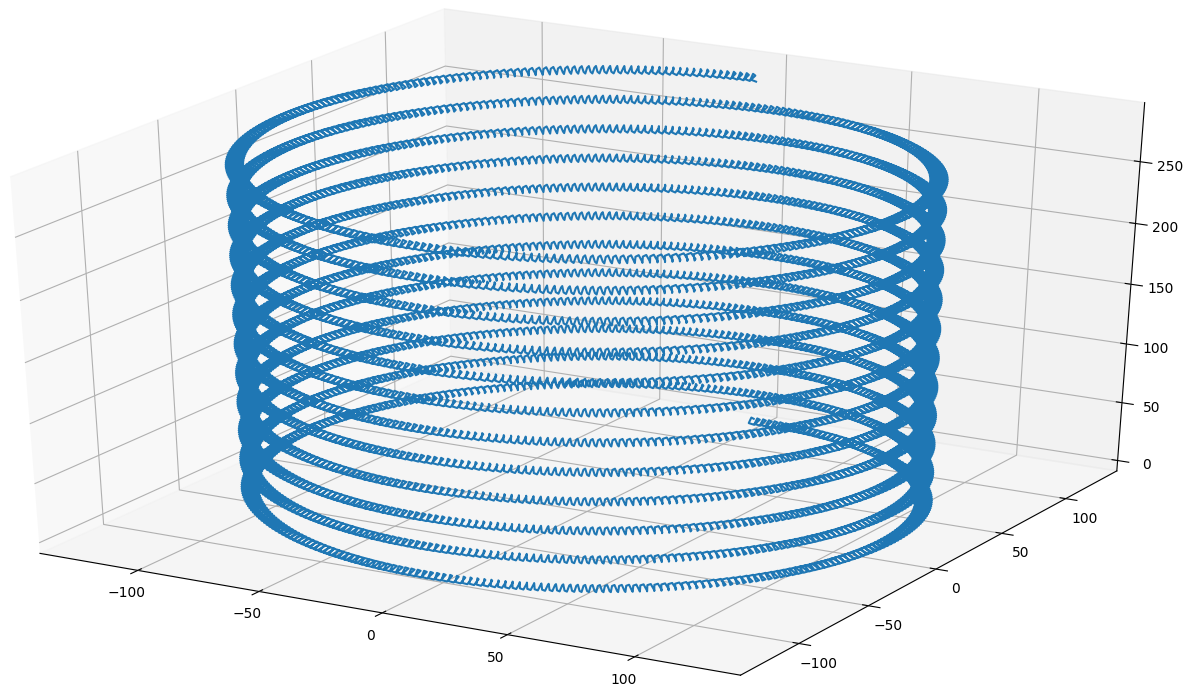
Python プログラムです。

import matplotlib as mpl
import numpy as np
import math
import matplotlib.pyplot as plt


# create
r1 = 3
x = []
y = []
z = []
for i in range(14400):
    dec = math.radians(i)
    deg = (i / 600) * np.pi
    r0 = 120 + r1 * np.cos(300 * deg)
    x.append(r0 * np.sin(deg))
    y.append(r0 * np.cos(deg))
    z.append(r1 * np.sin(300 * deg) + i / 50)


# plot
mpl.rcParams['legend.fontsize'] = 10

fig = plt.figure()
ax = fig.gca(projection='3d')
ax.plot(x, y, z, label='signal')
ax.legend()

plt.show()

なお数式以外は、ほぼパク…参考にして作成したものです。。。😅

◇　螺旋の螺旋の…

今度は可能な限り内部に螺旋を発生できるようにしてみました。

下のものができました。

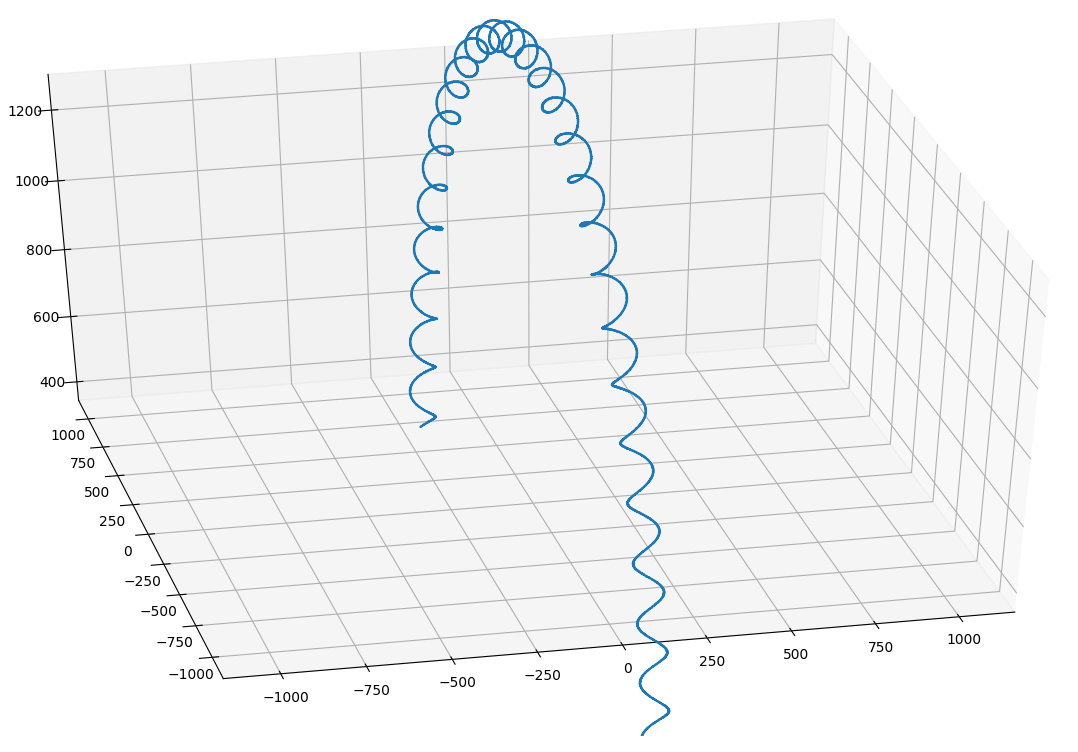
K：「なあ…なんか今までより小さくなってたいしたことないんじゃ…」

P：「…見た目を参考にするなといういい見本だ。今までのほうがよほど可愛かったぜ…」

計算も面倒でした。

考え方としましては、

①「螺旋の螺旋」で作ったものを、頑張ってもう一段だけ進化させる。

②進化させたものについて「なぜそのように進化させたのか」を考える。

　（ダブルループ学習）

本当は、四元数や行列計算でなんとかしたかったんですけども、直行平面が…とか、空間を回転させたら…とか考えてたら、どうも頭の中が螺旋状にねじくりかえってしまいました。

Python プログラムです。

import matplotlib as mpl
import numpy as np
import matplotlib.pyplot as plt
# import random
# import math
# from mpl_toolkits.mplot3d import Axes3D


def tr(xb, yb, zb, rb, dgb, t):
    dga = dgb / 60
    ra = rb / 40
    if dga > 12:
        r_st = tr(xb, yb, zb, ra, dga, t)
        xa = r_st['xa']
        ya = r_st['ya']
        za = r_st['za']
    else:
        xa = 0
        ya = 0
        za = 0
    rz = rb + ya
    d = (t / dgb) * np.pi
    zb = xa
    xb = rz * np.sin(d + za / rz)
    yb = rz * np.cos(d + za / rz)
    r_st = {'xa': xb, 'ya': yb, 'za': zb, 'ra': rb, 'dga': dgb, 't': t}
    return r_st


def main():
    dg = pow(60, 3) * 18
    r = pow(40, 2)
    x = []
    y = []
    z = []
    for t in range(dg):
        r_st = tr(0, 0, 0, r, dg, t)
        x.append(r_st['za'])
        y.append(r_st['ya'])
        z.append(r_st['xa'])
    # plot
    mpl.rcParams['legend.fontsize'] = 10
    fig = plt.figure()
    ax = fig.gca(projection='3d')
    ax.plot(x, y, z, label='ra-ra-ra')
    ax.legend()
    plt.xlim(-2000, 2000)
    plt.ylim(-2000, 2000)
    plt.show()


main()

再帰的処理を行えるよう関数型にしました。

if で再帰を制限してますが、外すことでほぼ乱数になるものの更に内部に螺旋を書けます。

「三角関数」と「三次元」と「配列」が揃って、ヘビー級に重くなりました。

最後でXとZを入れ替えたのは、そのままだと螺旋が横になってしまって、なんだか勢いがなくなって面白くなくなったからです。勢いは大事です。

なお、横にしたらなんとなくわかりますが上記は「完全な下ネタ🚀」です。

以下は、更に近づいた図です。

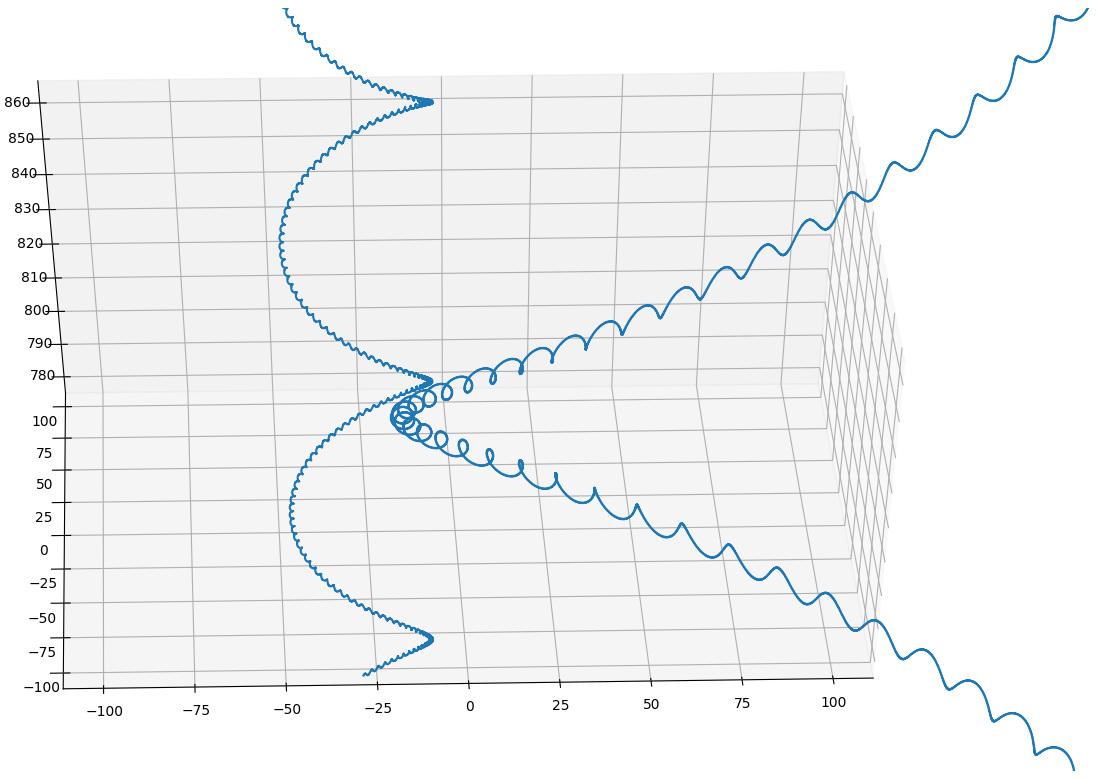
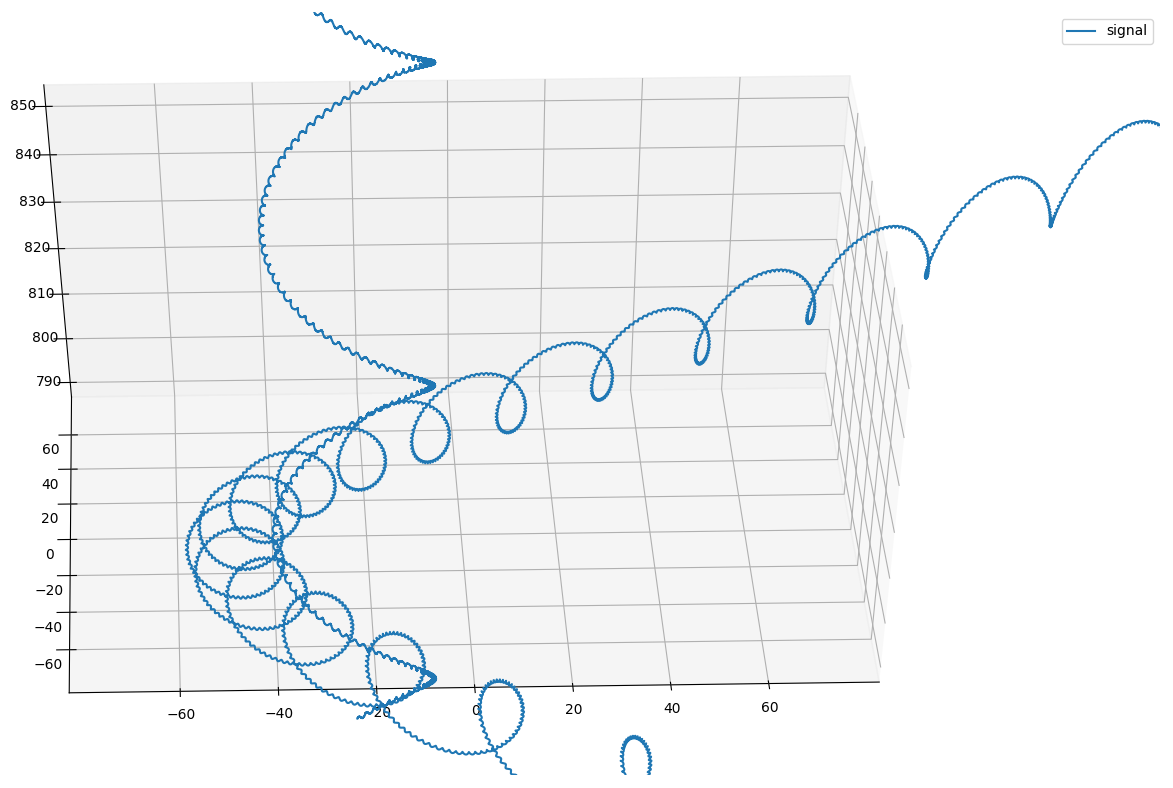
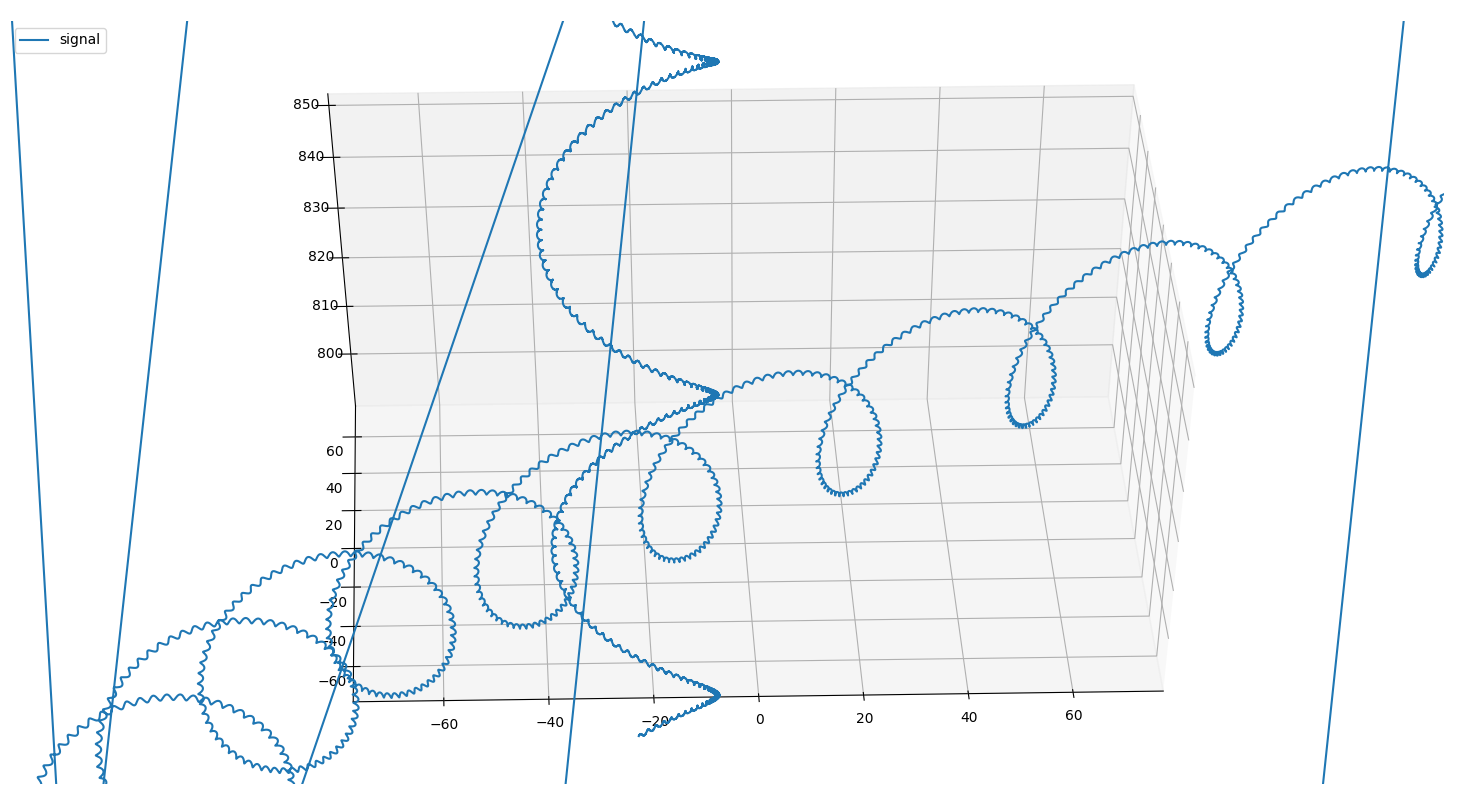
なんとかやっとで、螺旋の螺旋の螺旋のそのまた螺旋まで表示することができました。

◇　終わりに…

期待していたものと違ってたので、あまり面白みはなかったのですが、勉強にはなりました。三次元を扱う人は色々大変そうです。

それはそうと、これを電線と見立ててこれに高電圧⚡をかけたらどうなるんでしょうね。

コイルなので磁界が発生して、磁界が渦を巻いているので電界が発生して、電界によって電気が怒って…ええと…む、むむむむむ…（ゴゴゴゴ…）

「わからーーーん!!!!!（🌋ドッカーン!!!!!🌋）」

って大爆発したらいいですよね。

こんな難しいことは、頭のなかこんな螺旋でねじくりかえっているエキセレントな物理学者👽におまかせしたいですね。

💎おしまい💎