ずっと変わらないでいてほしい

昔、ファミ通で連載されていたユウジローの4コマ漫画だったかに、こういうのがあった。

小学生2人が、「殺す」ってどう書くんだっけ？と話していて、紙に「こうじゃない？」「いやこうだ」と、自分が思う「殺す」を書いていく。

途中で「あーもう分かんねー遊びにいこうぜ！」となって、机の上には微妙に間違った字で「殺す」といっぱい書かれた紙が残される。

最後のコマで、何も事情を知らない大人の人が通りかかって、その紙を見て「えー……どゆこと？俺を？」と戸惑う。

ただそれだけだ。

これが載ったのはおそらく1998年から2001年のどこかだったと思うが、時期についてはかなりうろ覚えなので、もうちょっと幅を広くとって、1997年から2005年のどこか、としておこう。

そもそも本当にファミ通だったのか、作者がユウジローだったのかも、うろ覚えだ。

やっぱり自分の記憶はあてにならない。

最近自分の記憶のあやふやさに驚いたのは『クラインの壺』(1989年発表) という小説についてである。

これを読んだのは1998年ごろ、つまり20年くらい前だ。今年 (2018年) の8月か9月になって内容をもう一度確認したくなって文庫版を買い直した。

この小説の中で、自分が乗っている車が本当に「同一」であるかどうかを確認するために、主人公がこっそり車内に10円玉でキズを付ける、というシーンがあったはずだと強く記憶していたのに、今回読み返してみるとそんなシーンはなかった。

まあ、似たシーンは、あるにはある。でも同一性の確認で重要なのは硬貨で付けたキズではなくピアスだった。

絶対あると思っていたシーンが無かったことに加えて、文庫版解説でさらに驚いた。解説を拾い読みしていたら突然「無線LAN」という言葉が目に飛び込んできたのだ。1998年当時、無線LANは一般的ではなかった。俺が今年になって買ったのは講談社文庫版 (2005年刊) で、20年前に読んだのは新潮文庫版だったのだ。「無線LAN」という言葉を目にするまで、俺はずっと20年前と「同一」の本を読んでいたと思っていたが、思わぬところに違いがあった。

ちなみにこの小説の後半のヒロインは『不思議の国のアリス』が好きだ。そういうわけで、バーチャル・リアリティとアリスを絡めるのは、『マトリックス』が最初ではない。

ところで、ある一つの行動が違う解釈をされることによる悲劇、というのは、アニメ史的には『伝説巨神イデオン』が有名なのだろう。

イデオンでは、白い旗が地球では「戦闘の意志がない」ことの表明だったが、地球とよく似た別の星では「相手を一人残らず殲滅する」という宣言であるという、異文化においてまったく別の解釈がなされることが原因で悲惨なことになった。

ただし俺はイデオンをいまだに観ていない。

さて、今回、俺はどうしても数学の話をしなければならない。

といっても難解な数式や論理式は出てこない。

「9800 × 1.08」という掛け算が分かれば十分だ。

重要なのは、この掛け算の数式とは一体なんなのか、ということだ。

いつの時代でも、掛け算が意味することは「同一」のはずだ。

消費税が8％から10％に変わるなら、上記の掛け算が持つ意味合いが変化するのではなく、単に「1.08」の部分が「1.1」になるだけだ。

消費税が変わろうが変わるまいが、「9800 × 1.08」が何を意味するかは不変である……ということになっている。

これは重大なことだ。法律は自然言語で記述されるが、時代によって言葉の意味が微妙に変わったり、社会通念が変化する。

数式の場合は、時代によって記号の意味が変わったり、社会通念によって解釈が変化したりはしない……ということになっている。

ちなみに、ホーキングは『ホーキング、宇宙を語る』(原著1988年刊) で、「数式を1つ登場させるごとに読者が半減する」と脅されて、「e = mc^2」だけを登場させたらしい。

ここでは、「^2」は2乗を表すと思っていてほしい。

加藤和也の『数論への招待』(2012年刊) のP.14には、以下のようなエピソードが紹介されている。

話は脱線しますが, 素数とx^2 + y^2 の関係について私的な経験を述べます. 私は大学院生の頃, 類体論を研究テーマにしていました. 歴史をやっている友人がいて, その友人を含め何人かで会った時, ある女性がその友人にどんな研究をしているかたずねますと, 友人は明治維新のことを話すのでした. 明治維新は黒船が来てから始まったのではなく, 江戸時代の農村にそのきざしがあった. 先日, 山梨県の旧家の屋根裏で古文書を調べてみると…, その家のおやじさんはおもしろい人で…」こういう話は誰でもフンフンと興味深く聞き入ってしまいます. そのあとその女性の「ではあなたはどんな研究を…」の声に, 私が「素数を x^2 + y^2 の形にあらわしてみたいのですが」と答えると, 「全然あらわしてみたくないんですけど」と言われてしまうのでした.

「同一」のエピソードを、別の視点 (加藤和也本人ではなく、教え子) から記述したものが以下にある。

http://www1.tmtv.ne.jp/~koyama/j_public.html

ところで今回、この本を紹介するつもりはなかった。

今回の記事を書いている途中で、この本に直接言及しないことが、何か奇妙な障害物を巧妙に避けながら書くようなものにならざるをえない、そういう状況に追い込まれていることに気づいた。

この記事が完成するまでの間に、様々な奇妙な偶然の一致との遭遇、沖縄に来てからの6年間の煤をはらう作業、などいろんなことがあった。

この世界は驚きに満ちていて、思わぬことがらが、途方もないレベルでつながっている。

昔から、俺が数学の基礎論にはっきり言葉で言及しようとすると、いろいろ奇妙なことが起こりやすくなる。もしこの記事が無事にALISのサイトに表示されていたとしたら、宇宙が新しいステージに移行した可能性がある。

それはともかく『数論への招待』では、素数のある不思議な性質について、以下のように記述している。

人間の世界では, ふたりの心に映る相手の姿は, 互いに無関係のことが多いようです. (実際, 私は若い頃, 先に紹介したガウスのラブレターをまねた手紙を書きましたが, 何の効果もありませんでした.) しかし, ガウスの心に映ったヨハンナさんの姿と, ヨハンナさんの心に映ったガウスの姿は, どちらも好ましいものであり, それはまるでガウス自身が証明した平方剰余の相互法則のようでした.

素数たちもお互いを深くわかりあっているのでしょう.

Aさんの心の中のBさんと現実のBさんが同一ではない、そしてBさんの心の中のAさんと現実のAさんが同一ではない。

あなたが想像していた「3つめの記事」と、実際のこの記事とはどれくらい「同一」だろうか。

構想段階での5月15日あたりの俺の心の中の「3つめの記事」と、実際のこの記事とはどれくらい「同一」だろうか。

書くのに5ヶ月もかかることになるなんて夢にも思わなかったので、少なくとも構想段階の時に描いていた完成までの道のりと実際の完成までの道のりの間には、とてつもないギャップがあったのは確かだ。

まあ、5ヶ月とはいっても、5ヶ月以上もの間ずっと推敲していたわけではなく、6月のはじめにほぼ書き上がってから何度も放置状態になっていただけなのだが。

さて、俺のALISの2つめの記事の内容を口頭で話すとしたら、

「インターネットはアメリカの軍事技術から生まれたって言われることがあるだろ？でもほんとは違うんだ」

みたいに始めることもできそうである。

今回の記事はというと、

「ブロックチェーンによってあらためて注目される『コードは法である』というアイディアについて、離散的かつ形式的な記述とは何かという観点から迫ってみたいのですが」

ということになるだろうか。でもこんな言い方をすれば、ほとんどの人には「全然迫ってみたくないんですけど」と言われてしまうだろう。

でもきっと今回の記事は、この言い方から想起されるほど味気ない内容にはなっていない……はずである。

さて、2018年になってからの日本では、政権与党やスポーツにおけるスキャンダルで「言った」「言わない」「そういう意図で言ったんじゃない」が問題になった。

ブロックチェーンはこういう問題を解決できるのではないかと見られている。

「言った」のか「言わない」のか、あるいは「何を言った」のか、はチェーンに何が書き込まれていたかを見ればいいわけである。

また、ハッシュ値だけを保存するようにすれば、発言の内容そのものを公開する必要はない。

2014年のSTAP細胞の騒動の時も、どの段階でどのデータが得られていたかが問題になった。

こういった生物学の研究でも、生データの画像のハッシュ値をチェーンに書き込んでおけば、「どんなに遅くてもこの頃にこういうデータが得られていたんだな」ということがあとから確認できる。

論文の体裁を整えるために画像を加工していたとしても、いざという時になれば「撮影当時の生データはこれこれで、ハッシュ値を何月何日にチェーンに書き込んでいました」と宣言できる。

もちろん、1ビットたがわず同じものを提示しないと、ハッシュ値による同一性の確認はできない。通常、データの中身が1ビットでも違うとハッシュ値はまったく違う値になるからだ。

「写真はあるんだけど、電気代の支払いの用紙が写り込んじゃっていたのでオリジナルのデータは公開できません」では話にならない。

これは写真のような「人間の意図」とは無関係の単なるデータについての話だが、「そういう意図で言ったんじゃない」のような、時と場合によってころころ解釈が変わるような発言についても、スマートコントラクトによって解決できるのではないかと言われている。

そもそも、ブロックチェーンはビザンチン将軍問題を解決するという触れ込みだった。ビザンチン将軍問題は、まさにこの「意図」が問題になる。

スマートコントラクトによって、約束事自体をコード (プログラミング言語による記述) として表現して、しかるべきタイミングで自動的に実行することが可能になる。

スマートコントラクトの基盤となるチェーンが、しかるべきタイミングでも「同一」であり続けさえすれば、期待した「約束」が自動的に実行される。

約束した時の本人と相手の両方が、その「しかるべきタイミング」の時点では死亡していたとしても、実行される。

これは凄いことだ。

約束を自動実行する、というのは別にブロックチェーンでないとできないことではない。

でもこれは、改竄が事実上不可能であるという性質と組み合わさった時に、強力な効果を生む。改竄が不可能であるということは、誰がいつどんなコード (約束) をチェーンに書き込んだかということを、例え当事者たちが死亡したあとであってもあとから確認できるということが凄いことなのである。

やろうと思えば、実行されるまでは約束事を公開したくない、というのも可能ではある。コードのハッシュ値だけを書き込んでおいて、実行するタイミングになってはじめてコードを公開する、というようなシステムも可能だからだ。ただしハッシュ値を書き込んでからコードの公開まで、バグ修正は一切できない。

これは遺言において有効かもしれない。「どんなに遅くてもこの時点でこういう意志を持っていた」と証明できると同時に、死亡時に何が実行されるかは実際に死ぬまでは公開したくない、というわけだ。でも遺言コードのチェーンへの自動書き込みが失敗して、残された人々も遺言コードの手動での書き込みを拒否したり遺言コードを紛失してしまったという場合には、遺言コードは実行されないということになる。

また、戸籍がチェーンで管理される状況であれば、「40歳の時点でお互いに配偶者がいなければ、自動的に籍が入るようにしたい、でもその時が来るまでそのことを公開したくない」というようなものも可能になる。この場合も、「2人とも40歳を超えた」「2人とも配偶者がいない」「2人とも生存している」という3つの条件に加えて、「コードが公開された」というもう1つの条件が揃った時に結婚するということになるわけなので、あんまり自動的という感じはしない。

ちなみに、自動的にコードをチェーンに書き込むということは、外部のサーバーなどに自動的に書き込むシステムが必要になり、結局は中央集権的なシステムに依存することになる。そのサーバーの管理者は、コードの中身を確認したり自動書き込みを阻止したりできるわけである。もちろん、複数のサーバーを用意することによる「難読化」はやろうと思えばできる。

まあでも、こういう話題、つまり今後ブロックチェーンでどんな応用が可能になるのか、といったことについては俺が書かなくてもいろんな人が書いてくれるだろうから、ここではコードとは何かということについてじっくり考えてみたい。

それにしても、コードとはいったい何だろうか。

ここで言うコードとは、何よりもまず、コンピュータのプログラムのソースコードのことだ。

「コード」は文脈によって意味がまったく変わる。暗号を指す場合もある。電源コードもコードだ。

自然言語では、同じ単語が別の意味を持つことは多い。これはなかなか困る状況だ。

同じ日本国内でも、方角という極めて実用的な言葉において、同じ単語が別々の意味になる場合がある。

「ニシ」という言葉が沖縄ではかつて「北」を指していて、今でも地名には残っている。

これはとても不思議で想像力がかき立てられる。

ニシは「去にし」だったかもしれないが、よく分からない。

関西あたりから見て西の方角で沖縄から見て北の方角というと、朝鮮半島や中国、あるいは対馬や済州島などが連想される。

関西だけでなく、九州からみて西で沖縄からみて北、ということになると、特に気になるのは済州島だ。

済州島は韓国本土とまったく違う文化を持ち、沖縄とも類似点が多いといわれる。

貴族や官僚や何らかの技術者集団がそういった場所から渡ってきて、任務終了後や死亡後に故郷へ「帰っていく」ことが繰り返されていたとしたら。

事情をよく知らない人から見れば「何やら重要人物がやってきて、死んだらあの方角へ帰っていった」という印象が深く刻まれることになる。

もちろんこれはなんの証拠もない、まったくの想像だ。

5000年くらい前は朝鮮半島や中国よりも南方の影響が強かったから、この説が正しいとすると5000年くらい前にはこの「去っていく方角」という発想は無かったはずということになる。でもそれを証明するのは容易ではない。

「ニシ」は自然言語での例だが、人工言語でも同じことは起こる。

人工言語の1つにSchemeというプログラミング言語がある。以下は、Schemeのコードだ。

(cond-expand

  (gauche (display "I like natto.\n"))

  (else (display "I hate natto.\n"))

)

Schemeのプログラムを実行するためのプログラム (実装系) はたくさんあり、そのうちの1つにGauche (ゴーシュ) というものがある。

前述のプログラムは、実装系がGaucheかそうでないかによって、まったく違う結果になる。

以下は、Gauche 0.9.5で実行した場合の出力結果だ。

$ gosh scheme_natto.scm

I like natto.

ちなみに「$」で始まっている1行目は、出力結果ではなく、どんな風にコマンドを実行したのかを示すために載せているものだ。

つまり、先程のプログラムを「scheme_natto.scm」という名前で保存し、「gosh scheme_natto.scm」とコマンドを入力したら、「I like natto.」と返ってきた、ということを意味している。

以下は、Guile 2.2で実行した場合の出力結果だ。

$ guile scheme_natto.scm

I hate natto.

今度は「I hate natto.」と返ってきた。

Guileでは、最初に実行した時にはコンパイル時のメッセージも一緒にずらずらと出力されるかもしれない。2回目以降の実行では、出力結果だけが表示されるはずだ。

これは同じ1つのプログラムが、解釈するもの (プログラムを解釈するプログラム) によって実行結果が異なる、という例である。

しかも実行結果は英語の文章で、その文章はまったく正反対の意味になってしまった。

ちなみにこの例は、「Gaucheの場合だけこういう風に出力する」と明確に記述されているプログラムなので、方言の違いによって思わぬ解釈の違いが生じた、というものとはちょっと違う。

それはともかく、コードとは何だろうか。

さて今後、プログラムのソースコードが何度も登場するが、意味の分からないところは飛ばして読んでほしい。

コードとは何かを考えるには、20世紀後半のアメリカではなく18世紀から20世紀前半にかけてのヨーロッパで起こったことに目を向ける必要があり、場合によっては歴史の「床板」を踏み抜く必要がある。

まず、当然のことながら、少数の記号によって複雑な構造を厳密に記述するという発想は数学で育まれた。

世間的なイメージとしても、数学は「不変」で「絶対」というものがある。数式や数学の証明は、それが持つ意味は人類が続く限り永遠に同じであり続けると。

科学の他の分野と違って、どんなに環境が激変したとしても、数学だけはずっと同じであり続けると。

しかし厳密性を追求すると、「同じ」とは何を指すのかというのは大問題である。

西洋哲学では「テセウスのパラドックス」あるいは「テセウスの船」と言われる有名な問題がある。

船のすべての部品が新しいものに置き換えられた時に、それは以前の船と同じ船だといえるのか、という問題である。

人間の場合も、細胞が常に入れ替わっている。ただし神経細胞は別だ。

そしてもちろんインターネットもまた、構成要素は常に入れ替わっている。

1997年のインターネットと、2018年現在のインターネットははたして同じなのだろうか？

おそらく1997年当時からは、ほぼ全てのサーバーやルーターが物理的に入れ替わっている。

ちょうど今月、2018年10月12日午前1時 (日本時間) にも、インターネット (特にWeb) にとって重要なシステムであるDNSの重要なアップデートが行われた。

それにしても、1997年当時の俺と2018年現在の俺は本当に同一人物なのだろうか。少なくとも俺には「記憶」はある。

バロウズは「これを書いたというはっきりした記憶がない」などと書いて物議をかもした。

さてここで、数学の話題に入る前に、この記事が生まれるまでの話をしよう。

少なくとも俺は、1つめ記事「仮想通貨の乱高下について」を書いた時のALIS、2つめの記事「新しい技術を規制するということ」を書いた時のALIS、そしていま3つめの記事をアップしようとしているALISを「同じもの」として扱っている。

こういう時、漠然と「同じだろう」と考えているか、そもそもそういうことに疑問を持たないかのどちらかだ。

運営が発信してる情報をつぶさにチェックしてるわけでもないし、システム内部がどうなっているかを覗いたわけでもない。

それでも、同じだとみなしている。

そして、ALISというシステムに保存されている個々の記事についても、同一性をあまり疑わない。

俺がこの3つめの記事をアップしようとしている2018年10月25日と、1つめの記事をアップした直後 (2018年5月6日) のそれぞれのタイミングにおいて、1つめの記事「仮想通貨の乱高下について」は本当に同一なのだろうか。

ALISのβ版が始まる少し前、公開後の記事の修正についてALISがどういう扱いをするのかについては気になっていた。

でもこれについては、俺がこの3つめの記事において書こうとしていたことと同様の指摘が、ALIS内ですでに以下の記事 (2018年5月16日公開) においてなされていた。

実際のところ、ALISが今後もずっと続いて、公開から10年くらい経った記事に、5000くらい「いいね」が付いているようなものをみかけた時、俺だったら何を考えるだろう？

この記事はいったい何回くらい修正されたのだろう？5年前も5000くらい「いいね」があったのだろうか？ここ数日で急に4000くらい「いいね」が増えたなんてことはあるのだろうか？

たぶんいろんなことを考える。

そしてそれはたぶん俺だけではない。

Wikipediaが (かろうじて) 信用されているのは、修正履歴が見られるからというのがある。

あるブログのエントリでWikipediaの記事に言及していた時、そのエントリがアップされた時期などから、「ブログ主はだいたいこのバージョンを見てたんだな」とあとから確認できる。

もちろん、過去の特定のバージョンに直接リンクすることもできる。

例えば、以下のURLは、英語版Wikipediaの「Hush-A-Phone」の2017年1月2日05:08のバージョンのURLである。俺がALISの1つめの記事「仮想通貨の乱高下について」を書いた時は、以下のバージョンを参照していたわけだ。

https://en.wikipedia.org/w/index.php?title=Hush-A-Phone&oldid=757867188

もちろんこれはWikipediaが、特定のバージョンへの直リンク (permalink) でアクセスした場合には誰に対しても「同一」の内容を表示してくれるはずという漠然とした信頼に依存している。

技術的には、特定の条件下で違う内容を表示するサイトを開設することはとても簡単だ。

渡辺浩弐がファミ通で連載していた短編小説でこういうのがあった。あるサイトには細工がされていて、特定の条件下でアクセスすると、毒を持ったある危険な植物のことを「食べても安全」と誤った情報が表示されるようになっていた。そして、安全というサイトの記載を鵜呑みにしてその植物を食べた人が死亡した。そういう架空の事件が描かれていた。もしかしたら植物ではなくキノコだったかもしれないが、うろ覚えである。

ちなみにこの小説ではさらに、ショートショートらしいオチが付いていた。

ALISの今後の方針は知らないが、先ほど紹介したALIS内の記事にあった

ALISのいいねは投稿した内容ではなく、記事のURLについてるのかな？

については、現状のALISはおそらくそうなっているが、記事のバージョンごとにpermalinkが発行されてそれぞれのバージョンの時代にいくつ「いいね」が付いたのか、というのをあとから確認できるような機能はあってもいいかもしれない、とは思う。

さらに言えば、「いいね」が急増した時期などがグラフで知ることができるようになるといいかもしれない。

例えばNHKスペシャルでALISのある記事が取り上げられたりしたとして、放送中のタイミングで「いいね」が急増していたりしたら、放送を見て慌てて「いいね」した人がいるんだろうなと想像がつく。

しかも分単位で「いいね」の増加が分かるようになっていて、その記事がとうてい数分で読み終わるような分量ではなかったという場合、明らかに読まずに「いいね」しやがった奴がいるなあ、ということまで分かる。

つまり、グラフによる増加の「傾向」と、「同一性」が維持されていたそれぞれの期間における「集計」が分かるようになれば、評価のされ方があとから判断しやすくなりALIS全体の信頼性も増すのではないかということである。

ところで、おそらく俺は、よほどのことがない限り、ALISで公開した1つめの記事 (5月6日公開) と2つめの記事 (5月14日公開) を今後 (つまり10月25日以降に) 修正することはない。

すでに公開したものが自分のものではなくなる感覚が生まれるまでには、必ずしも長い年月を必要としない。

別に記事が独り歩きしたわけではないものの、2018年10月25日現在、もうすでに1つめの記事と2つめの記事は「現在の僕とは全く別人の」、「ひとりの若者の作品」になってしまっている。

ところで、2つめの記事で「6年前」と書くべきところを「5年前」と書いてしまったのは、予期していなかったミスだった。

だが1つめの記事では、あることを仕込んでおいた。

大きな問題とはならない範囲内である修正を行って、しかもその修正履歴をはっきりと追記などの形で明記していない。

明記はしていないが、あとでネタにするために写真には撮っていた。

ところで今回、著作権的にギリギリ問題のない範囲内で画像を使ってみることにする。

俺は 99bitcoins.com がどのように運営されているかは全く知らないが、俺が2つめの記事を公開してから3つめの記事を公開するまでの間に、当然ながら「死亡回数」が変わっているはずだという確信があった。

ある意味では、これも2つめの記事に仕込んでおいたことといえる。

2018年10月25日現在、ビットコインの死亡回数は315回であり、2つめの記事を書いた時点の288回から変化している。

そして、本当に5月14日の時点で 99bitcoins.com での記述が288回になっていたのかを、もはや容易には確認できない。

また、2つめの記事をアップする時に、前述のものとは別のミスもあった。

1つめの記事をアップする直前にいろいろ実験したあと非公開にしていた、中身が空っぽの記事が「下書き」のリストにあったので、「せっかくだから」と、その空っぽの記事を使い回すという形でアップしてしまったのだ。

使い回したため、実際に書き上げたのは5月14日だったのに公開日が「2018/05/06」だったか何かになってしまい、慌てて非公開にしてあらためて記事を新規作成した。記事 (のURL) が生成されたタイミング、あるいは最初に公開したタイミングか何かが公開日として表示される仕様になっていたということを知らなかったのだ。

つまり、2つめの記事は、短い時間 (たぶん数分間) ではあるが、最初は別のURLで公開されていたということだ。

幸い、すぐに引っ込めたから、間違ったURLのほうで「いいね」をした人はいなかった。

「せっかくだから」は廃墟の中だけにしておきたいものだ。

それから、2つめの記事で引用した『コモンズ』P.54だが、実はちょっとだけ「改変」をしている。ここの「1956年」は、日本語版の書籍では「一九五六年」だった。これはGoogleブックスでも確認可能だ。

もう一点、引用には「(中略)」の問題がある。これだけでは、これが俺が入れた「(中略)」なのか、それとも書籍の段階で記述されていた「(中略)」をそのまま引用したのかが分からないのである。

HTML5のblockquoteタグの仕様上、これはしょうがない。

もちろん、引用者が挿入した情報であることを示すために、

<span class="added_by_the_quoter">(中略)</span>

などのような表明は可能ではある。でも現状のALISはタグを自由に記述できない。

記号的なことに関してなら、二重鉤括弧、つまり『』の使い方が「同一」でなかった。

2つめの記事の中の『ALISは死んだ』『ALISは終わった』のところが二重鉤括弧になっている必然性があまりない。

これは特に意識したわけでなく、あとから気づいた。

そういうわけで、たった2つの記事だけでも、これだけの「同一性」の問題が抽出できる。

ところで、このあと取り上げることになる大数学者のアンリ・ポアンカレは、自分の論文の中に論文の結論を全否定することになる致命的な誤りを見つけ、その論文が載った雑誌を自費で回収したことがある。しかも、その論文で獲得した懸賞金よりも大きな金額が、雑誌の回収・再発行にかかってしまったそうである。しかもその修正されたほうの論文は、カオス理論の源流とみなされている。

大きく歴史が動く時には、いろいろ香ばしいエピソードがつきものである。

そういえば、ポアンカレが敵視したカントールは、シェイクスピアとフランシス・ベーコン (画家じゃないほう) が同一人物であるという説に熱中し、本まで出した。

このベーコンと同一人物という説は、妄想的な人を惹き付けやすい定番のネタだったようで、要するに20世紀後半における「アポロ11号の月面着陸はNASAのでっちあげ」と似たようなものである。

シェイクスピア別人説自体は学術的な研究がなされているが、他者による改変や補筆というまさに「同一性」の問題により、特定を困難にしている。

2018年現在、社会的に問題となる「同一性」の話題は、本当に本人かどうかの確認の問題、つまり別人によるなりすましだとか、偽情報の拡散、偶然の一致などによって無関係の人物をパブリック・エネミー認定してしまう問題だろう。

偽情報の拡散や無関係の人物がパブリック・エネミーに認定されるのは、新しい形の災害といえる。

当事者の支援においては、人災なのか (悪意やミスによって引き起こされたのか)、天災なのか (偶然がもたらしたものなのか)、ということを判断しようとすると、当事者も支援する側も迷宮に入り込むことになる場合があるため、まず「災害である」ことを前提にする必要がある。彼らは「被害者」である前に「被災者」なのである。

本人確認は技術的にも社会的にも永遠の課題で、たとえ相手のことをよく知っていたとしても、気軽に物理的に会えない場合は厳密な本人確認はかなり難しい。

音声通話はもちろん、映像ももはや信用できない。

ディープラーニングによって、本人にそっくりな声・そっくりなしゃべり方・そっくりな表情を簡単に生成できるようになった。

もう今となっては、遠隔においては、「あいつが魔法少女と魔女っ子をまったく同一のものとして扱うはずがない」といったことでしか判断できない時代になってしまったのだ。

また、たとえ物理的に会っていたとしても、会えない時間が長かったりすると、脳内で極端に美化されていて「あの人じゃない」と判断してしまうこともあるかもしれない。

一度も会ったことがないけどTwitterアカウントを以前から知っている、というような場合なら、目の前でツイートしてもらうという方法はありそうだ。

確認したい側が、「『薔薇』と『ミネソタ州』と『マウンテンデュー』の3つの単語を含むツイートをしてください」などと口頭でお題を出して、そのとおりのツイートを目の前でしてくれたら本人確認成功だ。

お題は、2人の共通の話題からできるだけ離れて、偶然に一致する可能性がほぼ皆無であるようなものがいい。

「3時間後にこうこうこういうツイートしますので」と相手の方から申告されたものは本人確認にならない。

目の前にいるのは、どういうツイートをするかという情報をあらかじめ入手していた偽物かもしれないからだ。

また、1日に100回以上ツイートする人だと、偽物が不正にログインして行われたツイートが1つだけ紛れ込んでもそのまま気づかずに放置してしまう、ということもあるかもしれない。

ところで「対戦ゲーム」は、「eスポーツ」として別の文脈が与えられるようになって久しい。

レトロゲームにおいては、ゲームそのものの「同一性」が大問題となる。

最初からショーとしてのeスポーツを意識して作られたようなゲームは頻繁に変更が加えられるのでとりあえず置いておいて、レトロゲームの場合は歴史があり、「同じプレイを30年前にしていれば、30年前も同じスコアが出せたはず」というのが大前提となる。

最近も、有名なプレイヤーの不正が見つかって話題になった。

ドンキーコングの伝説の世界最高得点は不正操作によるものだった | TechCrunch Japan

https://jp.techcrunch.com/2018/05/02/2018-04-12-arcade-fame-turns-to-infamy-as-billy-mitchells-record-setting-donkey-kong-score-is-invalidated/

上記記事には、俺のために残しておいてくれたのかというような奇妙な誤字がある。英語原文のほうは正しいスペルだ。

この記事にもあるように、基板だと改造基板なのかどうかが分からない。

皮肉なことだが、レトロゲームの競技性を厳密に追求しようとすると、エミュレータによるプレイで競技するしかなくなるのではないかと思う。

エミュレータなら、ROMデータのハッシュ値によって同一性を確認できる。

そしてエミュレータなら、プレイヤーの入力情報をログとして残すことができ、ログデータが公開されていないものはハイスコアとみなさない、というルールにすることもできる。

そのログデータをエミュレータに食わせれば、誰でもそのプレイを手元のマシンで再現でき、実際にそのスコアになることを誰でも確認できる、というわけだ。

実際には、入力の情報だけではなく疑似乱数がどのように取り扱われたかのデータも必要になる。

エミュレータとログデータの公開でも不正の余地は残る。例えば、ゲームパッドに細工をする、などである。

でもこれも今なら技術的に解決できるのではないかと思う。

というのは、プレイヤーの手元を8Kくらいの画素数のデジタルハイスピードカメラで撮影し、ディープラーニングで解析すれば、「この手の動きでこのログデータになることはありえない」といったことが検証できるのではないかと思うからだ。ただし、ディープラーニングによる解析は実質的にブラックボックス化されており、誰でも検証できるものではない。

また、プレイ時において物理的に現場にいる「審判」への信頼は依然として必要となる。というのは、その手の動きの動画が改ざんされたものかどうかが分からないからだ。先ほど紹介したように、ディープラーニングで本人そっくりの顔の表情の動きを生成できるということは、ログデータから手の動きの映像を生成することもまた、可能だからだ。

ところで、世間的によくある誤解として、数学的営みとプログラミングを「同一」のものとみなす、というのがある。

数学には実にいろいろな誤解がある。

進化論を擁護した、1825年生まれのトマス・ヘンリー・ハクスリーという人がいた。

「1870年までは科学といえばハクスリー教授であった」といえるくらい影響力があったらしい。

彼は確かに科学を愛していたようだが、数学についてはひどい誤解をしていた。

1854年、つまり20代の時に以下のように書いている。

数学者はいくつかの一般命題から演繹するのに忙しいが、生物学者はそれにも増して観察、比較、および一般命題へ導くような過程にこそこだわりを持つ。これに疑義を挟む余地はない。

(中略)

数学者は対象物の二つの特性、数と広がりしか扱わず、彼が求めて帰納することのすべては何年も以前に形成され、完成されてしまっている。彼は今日では演繹と検証に他ならないことばかりにかかりきっている。

1868年、つまり40代の時には以下のように書いている。

数学者は彼らが問題に向かうときに用いるxやyなどを現実の存在物であると思い込んでいるに違いないのだが、科学の人が数学者の水準に身を置くときは、数学者に比べて不利な状態に堕すことになる。というのは、数学者がへまをやらかしたとしても実際的な結果に直面することはないが、体系的な物質主義が犯す間違いは、活力を麻痺させて一個の生命の美しさを破壊してしまうからだ

1854年のほうは、教育において押し付けられる「数学」と数学者による数学的営みをごっちゃにしており、1868年のほうは、科学における数学的基礎付けについて軽視しすぎている。

引用はそれぞれ『数学10大論争』からだが、皮肉なことに、ハクスリーの誤解を紹介するこの本の中で、本の著者も誤りを犯している。

「数学者のへま」を軽視すべきでない例として、1962年のNASAによる無人探索機マリナー1号の打ち上げ失敗の原因になった、「ハイフン」が欠けていたという有名なバグを挙げているのである。

これは例としてはちょっとまずい。

例えば「この暗号はこういう理由で安全である」と数学的に安全性を証明した論文においてその証明に不備があることが分かり、その暗号の脆弱性が明らかになった、そしてその暗号はネット社会で幅広く使われている暗号だった、というような場合ならば、数学におけるミスが現実世界に重大な影響をおよぼしたということになる。

でもハイフンが欠けているかどうかというのは、数学ではない。

これは数式を手書きで書き写す際に発生したミスであって、数学者による数学的な営みにおけるミスではない。

日本の奈良時代にも写経の誤字脱字を見つける仕事があったらしいが、写経の誤字脱字と仏教の教学的誤りは同一視しないほうがいいだろう。

ついでに言うなら、欠けていたのはハイフンではなくオーバーラインである。

さらに、これまた俺が今回の記事を書くために残しておいてくれたのかと思うようなネタとして、翻訳の際の誤りとして「マリーナ1号」になってしまっている。

もっとも、「Mariner」を「マリーナ」と表記すること自体は必ずしも誤りとはいえない。

ちなみに俺が確認したのは日本語訳の「2009年12月12日 第1刷発行」のものである。

ハクスリーの誤解については、同じ本の中で、数学者のジェームス・ジョセフ・シルベスターによる活き活きとした反論が紹介されている。

数学は、表紙の間に挟まれて真鍮の留め金で封じ込まれ、その内容をすみずみまで覚えようとひたすら辛抱強く努めるほかない、といった書物ではない。それは、そのなかの宝物を手にするまでに長くかけて精錬しなければならないにもかかわらず、著しく限られた鉱脈や裂け目にしか含まれていないといった鉱石ではない。それは、その豊穣さが連作を続ければ失われてしまうような土壌ではない。それは、その領域が地図に描きとめられ、その輪郭が定められてしまうような大陸ないし海洋ではない。

それは際限がなく、その有り様は、あたかもその大いなる意欲が向かうには狭すぎるやも知れない空間のようである。その可能性たるや、宇宙飛行士が目を見開いて眺めるたびにいつまでも広がりつづけ、幾重にも増大しつづける世界のように果てしない。それは、指定された境界のうちに封じ込まれてしまうことも、永遠に有効ないくつかの定義に帰着されてしまうこともあり得ない。あたかも、おのおのの単子 (モナド) のなかに、物質の各原子のなかに、葉やつぼみや細胞のひとつひとつのなかにまどろんでいながら、時あらば野菜や動物といった新しい形態へと発生していくために絶えず備えつづけている意志、すなわち、生命のごとくである。

ちなみに、『数学10大論争』の原著 (英語版) では「あたかも、」以降は省かれて引用されていたらしい。

形式的記述は「生命のごとく」の数学の中で育まれ、19世紀の基礎論の勃興によってもう一度練り上げられ、現代のコンピュータのプログラミング環境に強い影響を与えた。影響を与えたというか、母体になったといってもいい。

以下は、2の平方根、つまり√2を1桁ずつ泥臭く計算するRubyのプログラムである。

#!/usr/bin/ruby

require 'bigdecimal'

original_num = 2

# integer part

integer_part = 0

loop do

  candidate = integer_part + 1

  break if (candidate ** 2) > original_num

  integer_part = candidate

end

sqrt_str = "#{integer_part}."

# decimal part

loop do

  last_digit = 0

  9.times do

    candidate = "#{sqrt_str}#{last_digit + 1}"

    break if (BigDecimal(candidate) ** 2) > original_num

    last_digit = last_digit + 1

  end

  sqrt_str = "#{sqrt_str}#{last_digit}"

  puts sqrt_str

  sleep 0.2

end

実行すると、以下のように、0.2秒ごとに1桁ずつ増えたバージョンを強制終了されるまでひたすら出力し続ける。

$ ./sqrt2.rb

1.4

1.41

1.414

1.4142

1.41421

1.414213

1.4142135

1.41421356

1.414213562

1.4142135623

ここで注目してほしいのは、ループを使うことにより、有限個の文字で2の平方根という無理数を「表現」していることだ。

理論上、無限回計算すれば「正確な」平方根が出力される日が来る、とみなすことができる。

つまり、有限個の記号で表現されたプログラムによって、√2が定義できているとみなすこともできる。

ただし、あるメソッドが可能な限り正確な値を返そうとしていたとしても、そのメソッドを呼び出す側のコードも含めて考えてみると、有限時間内に計算し終わらないのでシステム全体としてはやっぱり定義できていないことになる。

ちなみに上記プログラムの「original_num = 2」を「original_num = 9」に書き換えると、2の平方根ではなく9の平方根を求めるプログラムになる。

書き換えてから実行してみると、以下のように出力される。

$ ./sqrt9.rb

3.0

3.00

3.000

3.0000

3.00000

3.000000

3.0000000

3.00000000

3.000000000

3.0000000000

3 × 3 = 9 なので、当然何回計算してもずっと0が続くだろう。

でもそれは本当なのだろうか？

本当にこのままずっとずっと永遠に0が続くのか？

もしかして10億桁目に突然「5」が現れて我々の度肝を抜いたりしないのか？

少なくとも俺は実際に実行して確認したりはしていない。

エンジニア的な発想では、もし突然「5」が現れたりしたら、メモリ残量が逼迫してきた時にRubyのBigDecimalの挙動が不安定になるのではないか、ということをまず疑うことになるだろう。

このコードはものすごく泥臭く計算しているので、平方根にまつわる数学的知見というものをほぼまったく使っていない。「2乗すると元の数 (original_num) になる」ということしか使ってないともいえる。

3 × 3 = 9 であることを「証明不要」であるとみなしたとしても、3 × 3 = 9 であるということと、このプログラムが本当に「0」を出力し続けるかどうかということとは、数学的にもエンジニアリング的にもそれなりの隔たりがある。

ところで、先ほどは同じコードが同じ言語でも処理系が違うと違う結果を出力するという例を挙げたが、今度は、まったく「同一」のコードなのに、まったく別のプログラミング言語としても解釈できるものを書いてみる。

しかも、単に解釈できるというだけでなく、別のプログラミング言語として解釈しても、同じ結果を出力する。

例えば以下のコードは、Rubyとして解釈しても、JavaScriptとして解釈しても、同じ結果を出力する。

"#{class Console; def log(s) puts s end; end}"

"#{console = Console.new}"

console.log("hello, ALIS");

実際に動かしてみる。

Ruby2.5.1で動かした場合。

$ ruby cheshire_code1.txt

hello, ALIS

JavaScript (Node.js 8.10.0) で動かした場合。

$ nodejs cheshire_code1.txt

hello, ALIS

上記の場合は、実行する時にどのプログラミング言語で実行するかを手動で指定している。

では、以下のようなシェルスクリプトを用意してみよう。

#!/bin/sh -

second=`date +%S`

if [ `expr $second % 2` -eq 0 ]; then

  /usr/bin/env ruby "$@"

else

  /usr/bin/env nodejs "$@"

fi

このコードは、偶数秒の時は「cheshire_code1.txt」をRubyで実行し、奇数秒の時は「cheshire_code1.txt」をJavaScript (Node.js) で実行する。

このシェルスクリプトのファイル名を「cheshire.sh」にし、実行権限を付与し、先ほどの「cheshire_code1.txt」と同じディレクトリに置いてみる。

実行すると、やはり「hello, ALIS」と出力する。

$ ./cheshire.sh cheshire_code1.txt

hello, ALIS

でも出力だけを見る限り、Rubyとして解釈された出力結果なのかJavaScriptとして解釈された出力結果なのかを知ることはできない。

「プログラムを解釈するプログラム」が、RubyだったのかNode.jsだったのかを知ることができない。

RubyとJavaScriptは関数型言語が再注目される中でその言語的特性が再評価・再解釈されるようになった。

でもRubyとJavaScriptは決して似ているわけではない。

この2つは進化の過程も文法もまったく異なる言語だ。それでもこの「cheshire_code1.txt」のように、どちらの言語としても解釈できるプログラムが書ける。

しかも自然言語にありがちな「解釈できなくはない」というものではなく、どちらの言語だと解釈しても「厳密に」文法的に正しい。

それでも古今東西のあらゆるプログラミング言語を思い浮かべてみれば、RubyとJavaScriptはとても似ているということになってしまうかもしれない。

アメーバ、ピパピパ、ダツ、ラフレシア、犬、猫、の6つの生物を並べてみれば、犬と猫はほとんど同じ生物だ、といえるのと似たようなものだ。

というわけで、RubyとJavaScriptだけでなく、さらにScheme (Gauche 0.9.5 や Guile 2.2.3) として解釈しても同じ出力をするバージョンを書いてみた。

;"#{class Console; def log(s) puts s; end; end}";

;"#{console = Console.new}";

;s = `

exit

(display "hello, ALIS\n")

;`

;console.log("hello, ALIS");

実行してみる。

$ ruby cheshire_code2.txt

hello, ALIS

$ nodejs cheshire_code2.txt

hello, ALIS

$ gosh cheshire_code2.txt

hello, ALIS

$ guile cheshire_code2.txt

hello, ALIS

このバージョンは、Rubyで実行した時には一部がシェルに渡されるので、シェルスクリプトというさらに別の言語も絡んでくることになる。

それにしてもこの「cheshire_code2.txt」、これはちょっとズルいのではないかと思う人もいるだろう。

というのは、コードの中に「hello, ALIS」が2回登場しているからだ。

こんなのがアリなら、cheshire_code1.txt も、

"#{puts 'hello, ALIS';exit}"

console.log("hello, ALIS");

みたいに書けた。

というわけで、cheshire_code2.txt を修正し、コードの中に「hello, ALIS」が1回だけ登場するバージョンも書いてみた。

;"#{class Console; def log(s) puts s; end; end}";

;"#{console = Console.new}";

;"#{class String; def replace(obj, obj2) self; end; end}";

;s=`

#(

display() {

printf "$1"

}

false ; ( false

)

(display "hello, ALIS\n")

exit

;`

;s = s.replace(/(\n|.)*\n\n/, "");

;s = s.replace(/[^"]*"(.*)(\n|.)*/, "$1");

;console.log(s);

だいぶ黒魔術っぽくなってきた。

このコードは、中盤あたりはSchemeとしてもシェルスクリプトとしても解釈できるようになっており、結局4つの言語の特性を活用している。/bin/sh がdashでない場合は、Rubyの時にうまく動かないかもしれない。

ちなみにSchemeでは「;」で始まる行はすべてコメントとして解釈されるので、Schemeの場合はコードの中盤あたり以外はすべて無視されている。

こういうコードで面白いのは、1行あたりが長い部分は、正規表現やクラス定義のおかげで長くなっているだけであってたいして黒魔術的なわけではなく、2文字だけとか4文字だけとかの行のほうが黒魔術的要素が濃いことだ。

「難解な数式や論理式は出てこない」と約束したのに、コードについては複雑なものが出てきてしまった。

こういう話題はヒマ人や曲芸師が薄暗い部屋でひっそりと楽しむものであって現実世界には何の影響も及ぼさないようにも見えるが、そうともいえない。

例えば、2005年にCSSXSSというバグが話題になった。

これは当時のIE6が外部リソースを読み込む際に、ものすごく好意的にスタイルシートとして解釈してしまうために、意図しない情報漏洩が引き起こされるというものだった。

HTMLをCSSとして解釈してしまうことが、セキュリティ上の問題になったわけだ。

漢字やカタカナなどを構成するバイトをCSSの構造化のための文字として解釈してしまっていたために、さらにセキュリティ上の脅威が増していた。

つまり、漢字やカタカナなどをどのように表現するかというもう1つの「コード化」も関わっていたわけだ。

今回の記事をここまでじっくり読み進んできた読者なら、当時俺が本当は何を面白がっていたのかというのがお分かりいただけるのではないかと思う。

CSSXSSでもう一つ重要なのは「ロバストネス原則は過去のものになった」という確信だったが、これについては当時とは俺自身の考えが変わっている部分もあり、これはまた別の機会に掘り下げることにする。

さて、セキュリティ上の問題というのは、設計上の問題や設定ミスやヒューマンエラーでないなら、たいていはコードのミスだ。

でも「このコードには誤りがある」という言明があった時に、それが何を意味するのかは、無数の暗黙の前提に依存している。

この記事のこれまでの流れからみれば、そのコードとは、チューリング完全なプログラミング言語か、HTMLやCSSなどのデータ形式を指すということになりそうだ。

でも、もっと身近で、ほとんど誰もが使ったことがあり、書いたことがあり、ほとんど誰もが厳密に形式的に運用した経験のあるものがある。

例えば、整数をあらわす数字。

「数字」と「数」は違う、とよく言われるが、数字とは数をコード化したものだといえる。

「5 + 5 = 10」は、5に5を加えるという「計算」の「結果」が10である、と、算数では解釈される。

でもそれは本当だろうか。

そもそも「10」とは何だろうか。16進数における「10」とは、10進数では「16」である。

16進数ではよく、10進数における「11」を「a」、「12」を「b」、というように、アルファベットを使う。

そういう「コード」のルールなら、「5 + 5 = 10」は16進数では「5 + 5 = a」となる。

ここで、先ほどの「同じコードが、別のプログラミング言語でも解釈可能」というのを思い出してみよう。

Rubyとして解釈してもJavaScriptとして解釈しても文法的に正しいコードを先ほど示した。

同じように、アルファベットが含まれていなければ、その数字は10進数としても16進数としても解釈できるコード、ということになる。

でもこれだけでは、Rubyのような言語とただの数字を比較するのは強引すぎると感じる人もいるだろう。

そういうわけで、実際に整数という「コード」を実行するプログラムをつくってみよう。

ここでの「整数」の「ソースコード」は、この記事の中で登場する実際に動作するコードの中で、最も単純なものといえる。なんせ「0」だけでも立派なコードなのだ。

#!/usr/bin/env ruby

if ARGV[0] !~ /\A[0-9]+\z/

  $stderr.puts 'syntax error'

  exit

end

puts '+' * ARGV[0].to_i

実際に実行してみる。「5」というコードを実行すれば5個の「+」が、「10」というコードを実行すれば10個の「+」が出力されるはずだ。

$ ./code10.rb '5'

+++++

$ ./code10.rb '10'

++++++++++

実際に「+」の数を数えてみれば確かに5個と10個になっているはずだ。

ruby -e 'puts "hello, ALIS"'

みたいなのをワンライナーという。これは「puts "hello, ALIS"」という1行だけのプログラムをRubyで実行する。

この「code10.rb」の場合は、ワンライナーしか書けない実装系だといえる。

そして16進数バージョンも書いてみた。

#!/usr/bin/env ruby

if ARGV[0] !~ /\A[0-9aAbBcCdDeEfF]+\z/

  $stderr.puts 'syntax error'

  exit

end

puts '+' * ARGV[0].to_i(16)

今度は、「5」なら先ほどと同じように5個だが、「10」なら16個になるはずだ。

$ ./code16.rb '5'

+++++

$ ./code16.rb '10'

++++++++++++++++

16進数として解釈した時と10進数として解釈した時とで「実行結果」が同じになるコード、というのはつまり、0〜9の10個だけである。

正確には、実行結果が同じで、かつ、どちらで解釈した場合でも文法的に正しいコードは10個だけ、といえる。

$ ./code10.rb '7'

+++++++

$ ./code16.rb '7'

+++++++

しかしこの「code10.rb」や「code16.rb」は、Rubyが整数を「知っている」ことを利用してしまっている。これはちょっとズルいのではないだろうか。

というわけで、Rubyがあらかじめ知っている整数の性質を、あえて直接的には一切使わずに「code10.rb」を書き直してみた。

#!/usr/bin/env ruby

if ARGV.find{true} !~ /\A[0-9]+\z/

  $stderr.puts 'syntax error'

  exit

end

code = ARGV.find{true}

h = Hash.new

h['0'] = ''

h['1'] = "#{h['0']}+"

h['2'] = "#{h['1']}+"

h['3'] = "#{h['2']}+"

h['4'] = "#{h['3']}+"

h['5'] = "#{h['4']}+"

h['6'] = "#{h['5']}+"

h['7'] = "#{h['6']}+"

h['8'] = "#{h['7']}+"

h['9'] = "#{h['8']}+"

remaining_code = code

while remaining_code != '' do

  current_str = remaining_code[/^./]

  current_digit = h[current_str]

  remaining_code = remaining_code.sub(/^./, '')

  stored = current_digit

  i = remaining_code

  while i != ''

    j = h['9']

    tmp = ''

    while j != ''

      tmp = "#{tmp}#{stored}"

      j = j.sub(/^./, '')

    end

    stored = "#{stored}#{tmp}"

    i = i.sub(/^./, '')

  end

  print stored

end

puts

まったくRubyらしくない異様なコードだ。

でもRubyが知っている整数というものを一切使わないならこのようにならざるをえない。

iやjはたしかにループ変数なのだが、実際に格納してるのは文字列で、しかも文字列の中身は見ずに文字数だけを利用している。

iやjを使っているところは文字数の分だけループを回せばいいだけなので「String#each_char」を使えば多少はRubyらしくなるが、ブロックなしだとEnumeratorを返すようなものは、ここではなるべく使いたくない。「str.length.times」なんてもってのほかである。

「ARGV.find{true}」だって、断腸の思いでやっているのである。

ちなみに、文法エラー判定を変更し、「h['9']」で終わっているところを「h['f']」まで定義し、「j = h['9']」の部分を「j = h['f']」に変更するだけで、16進数バージョンになる。

ここまで来れば、先ほどの「5 + 5 = 10」などの足し算も、「10」というコードががただの計算結果ではないということが実感できるのではないかと思う。

我々は無意識のうちに、何らかの形で「整数をあらわす数字」というコードを「パース」し「実行」していたのである。

こうしてみると、「5 + 5」も「10」も、それぞれ数を別の方法でコード化しているだけで、どちらかがどちらかの「結果」ではないということになる。

つまり、トートロジー。

あるいは、現代的なプログラミング環境の用語でいうなら、四則演算というやや複雑な言語の中に整数というシンプルなDSL (domain-specific language) があるのだ、とも解釈できる。Rubyの中に正規表現というDSLがあったり、HTMLの中にインラインでCSSを書いたりできるのと似ているわけだ。

さてここで、関係を図でみてみよう。

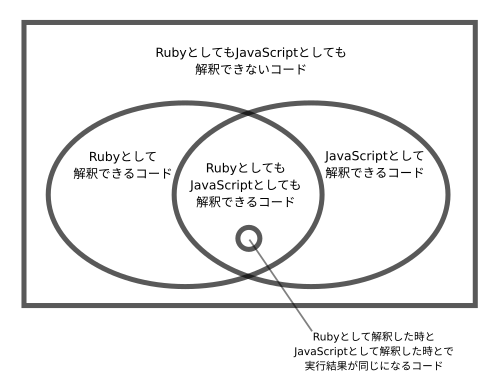
先ほどの「cheshire_code1.txt」などは、上の図の小さい丸の中にあるということだ。

次に、整数をあらわす数字についても図でみてみよう。

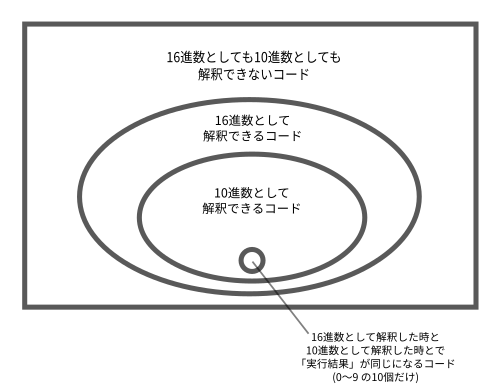
こっちの図の小さい丸の中に入るコードは10個だけだが、先ほどの図の小さい丸の中に入るコードは、理論上は無限個ある。

整数のほうも、先頭に「0」を追加するのをアリだとすると、10個ではなくやはり無限個になる。実は先ほどの整数を「実行」するコードも、先頭に「0」を追加しても動作する。

さて、もし基礎論の洗礼を受けていないにも関わらず、ここまで読み進めてきて「数」というのは定義が難しい存在なのではないか、と感じた人がいたら、それは勘の良い人だ。

19世紀において、数をどうやって定義するのかという問題、無限をどう扱うのかという問題、様々なパラドックスの発見、数学基礎論の勃興、これらは複雑に絡み合っていた。

『数論への招待』P.122 には以下のようにある。

さて無理数の発見は, ユークリッドの『原論』の構成, つまり当時の数学全体の構成法, に大きな影響を与えました. 『原論』は, 5つの公準を出発点にしてそこから証明をつみあげていく形をとっていますが, その公準は,

公準1 与えられた2点を通る直線をひくこと (ができる).

公準3 与えられた点を中心とし, 与えられた長さの半径を持つ円を描くこと (ができる).

など, すべて図形に関するもので, 『原論』全体が図形を相手にする幾何学の丁裁をとっています. 数を基礎にせず, 図形を基礎にして, 数学を構成していったのは, 無理数が発見されて意外に複雑な数の世界の素顔が現れてきた以上, 単純なことを基礎にして証明をつみあげていくには図形の単純な性質から始めるのが最善だと考えたのだと思われます.

ちなみに「丁裁」は「原文ママ」である。

古代ギリシャのユークリッドの『原論』の「発生」は、欧米ではキリスト誕生に匹敵する出来事だ。

その『原論』では、数ではなく図形によって数学全体を基礎づけているのである。

『数論への招待』では、もし仮に図形ではなく自然数の定義から『原論』が始まっていたらという仮定にふれたあと、以下のように続ける。

しかしこのように自然数の導入から『原論』をはじめてしまったら, √2などの無理数をどうとらえるのかが, のっけから非常に難解な議論になってしまうので, 基礎としては図形をとったものと思われます. (図形から始めれば, √2は1辺の長さが1の正方形の斜辺の長さとして, 単純でとらえやすい存在です.)

数学を根本の所から考え, それを自然界の原理と結びつけて考えていた古代ギリシャの学問において, 有理数でない数が存在することをどう理解するかは, ゆるがせにできない問題でした.

図形は直感的でとらえやすく、子供にも教えやすい。

非常に少数の前提 (公理) からスタートしてすべての複雑な数学の定理を証明していくというスタイルは、19世紀以降の数学に大きな影響を与え、現代のコンピュータ環境にも影響を与えている。

19世紀前半において非ユークリッド幾何学が誕生したのは、『原論』の5つの公準のうちの1つが成り立たない世界を仮定して誕生した。これによって、「前提を問う」ということが市民権を得たともいえる。

でも古代ギリシャにおいて、『原論』の公理 (公準) がまったく自明なものと捉えられていたのかというと、そうでもないかもしれない。

2007年刊の『無限のスーパーレッスン』P.143 には以下のようにある。

「(中略) 今日はまず、『公理とは仮定に過ぎない』という考え方が19世紀の新発見ではなく、古代ギリシアにすでにあったのが忘れられていただけで、実際のところは古代の知恵の再発見に過ぎないのである、とする20世紀のハンガリーの数学史学者、サボーさんの説をご紹介することから始めたいと思います」

(中略)

「公理から数学体系を構築していく、というやり口が意外にも19世紀以前ではユークリッドの原論以外にほとんど見当たらないんですよ。物理でなら、ニュートンが力学理論を発表した『プリンキピア』がユークリッド原論のスタイルで書かれたりしているんですけどね。1903年にラッセルとホワイトヘッドが『プリンキピア・マセマティカ』で公理から集合論の土台の上に数学を築こうとしたのが、物理からの逆輸入だった、というわけです。(中略)」

「(中略) で、サボーさんの理論なんですが、なぜギリシア時代なんて大昔に、あれほど厳密に論理的に完成されたユークリッド原論を書く事ができたのか？ その秘密は、アキレスと亀の話を編み出したエレア学派にある、と言うんです」

(中略)

「ユークリッドは、ソクラテス、プラトン、アリストテレスたち同様ピタゴラス学派、という研究グループの一員だったはずなんですが、ピタゴラス学派の作図に対して、きっとエレア学派が同じようないちゃもんを付けたはずだ、とサボーさんは言うんですよ。それでしょうがないので、『線で結べる』というのを議論の前提として認めさせよう、と。で、それさえ認めさせてしまえばあとはこっちのものだっていうわけで」

「話としては面白いけど、証拠はあるのかしら？ サボーさんの説って定説として認められているわけ？」

「中根先生という数学史の専門家にお尋ねしてみたのですが、どうもまだいくつかある説の一つに過ぎない、ということのようです。でも僕はこのサボーさんの理論に心酔しているので、その理論にしたがって話をさせて下さい。証拠の一つとしては、たとえば『公準』という訳語の横に『(要請)』ってなってますよね。これは『公準』という単語アイテーマタが、『お願いする』という意味なんだそうです。『とりあえず2点を定規で結べるっていうことは認めてね、お願い、お願い』というわけです。もう一つの証拠は、平行線公理の話で出てきた5世紀の数学者プロクロスさんがユークリッドの原論について解説しているのですが、その中で公準の1番目から3番目までについて、『もし誰かが、運動のない幾何学の世界に線を引くとか円を描くとかの運動をどうして持ち込めるのか、なんていちゃもんを付けてきたら、お願いだからそんなことに思い悩まないで、と答えましょう、という意味なのだ』と説明しているんですね。つまり、そんないちゃもんを付けてきた奴らがいたから、こんな公理を準備したのだ、と読み取れるわけです。 (中略) ユークリッドの原論にはあまり論理的に厳密にやらずにいい加減に済ませているところもたくさんあるんですよ。ところがエレア学派に攻撃されそうなところだけは、ちゃんと守りが固めてある。これはまさしくエレア学派と激しく戦った結果が、このような公準として残されたんだ、と言うんです」

もしかしたら1903年に書き始めたという意味なのかもしれないが、1903年に出たのは『数学の諸原理』(The Principles of Mathematics) のほうで、『プリンキピア・マテマティカ』(Principia Mathematica) の第1巻が出たのは1910年である。

紙の書籍でもWeb上の記事でも、この2つを混同しているものは多い。

この『プリンキピア・マテマティカ』は少数の公理と推論規則からスタートして「1 + 1 = 2」を証明するのにまるまる本1冊を費やして、様々な激しい反応を引き起こした。

それはともかく、ユークリッドの『原論』が数ではなく図形から始まっているという点と『原論』の公理系のあり方に論争の形跡がある点については、「数学考古学」にとっては重大な問題である。

それは、幾何学的直感を重視するのかそれとも離散的な記号で基礎付けるのかという19世紀から20世紀前半にかけての大騒動が、実際には古代ギリシャですでにあった論争の再燃だった可能性が高いからだ。

ところでこの『無限のスーパーレッスン』は、まさにシルベスターがいう「数学は、表紙の間に挟まれて真鍮の留め金で封じ込まれ、その内容をすみずみまで覚えようとひたすら辛抱強く努めるほかない、といった書物ではない」ことを感じることができる好例だ。しかも前提知識は不要だ。

この本の真の主役は、明らかにゲーデルではなくヒルベルトなのだが、ヒルベルトの独創性については美化されすぎているので、そこは差し引いて読む必要がある。

ヒルベルトの極端な美化は数学者集団のブルバキの影響も大きい。

20世紀には、確かに「ブルバキ化 or DIE」みたいな空気があったようだ。

『ヒルベルトの挑戦』P.240 には以下のようにある。

ローチは、ブルバキを読むのは干し草を噛むように味気がないと言った。それでいて、ブルバキがやろうとしていることを強く支持した。「これは、19世紀の数学というよどんだ遺物を根こそぎにするという意味で、非常に計り知れない価値があると思われる動きだ……」。そして、数学者は最終的には「ブルバキ主義者になるか、ちがう道を行き19世紀というかつて栄えていたオアシスをさまようか」のどちらかを選ばなくてはならないと述べた。

(中略)

メンバーはまた、共通した数学の哲学をもっていた。その中心にはヒルベルトが据えられ、まさに模範とされていた。ただし、おそらくは自覚している以上に、そのヒルベルト像は自分たちの目的にかなうように脚色されていた。数学を公理的に提示した点がヒルベルトの代表的な業績だと熱心に唱え、これこそが数学への最大の貢献だと考えた。

「ローチ」とはコロンビア大学教授だったEdgar Lorch (1907 - 1990) のことである。また、「メンバー」とはブルバキの面々のことである。

ヒルベルトの発想を象徴する有名な例えとして、「点」「直線」「平面」と言う代わりに、「テーブル」「椅子」「ビールジョッキ」と置き換えても意味が通るようにしなければならない、というのがある。

これはヒルベルトがヘルマン・ウィーナーの講義を受けたことをきっかけとして生まれた発想といわれる。

現代的なプログラミング環境で類似点を探すなら、クラス名や変数名は何であっても動作は変わらない、というのがまず浮かぶだろう。

先ほどの整数コードを実行するプログラムの中で、「i」や「j」という変数を登場させた。

FORTRANの時代には「I」や「J」を使うことに意味があったが、Rubyでは特別な意味はない。ただ人間に対して「ループ変数ですよ」と分かりやすくするためだけに使っている。

コンピュータ (Rubyの実装系) にとっては、「i」や「j」が何を指すか、どのような目的で使われるか、というのはどうでもいい。ただひたすらに決められた手順で、書かれたプログラムを実行していくだけだ。「i」や「j」を「table」や「chair」に変更しても、問題なく動く。

数学全体を、現実世界の直感から離れて記号的なゲームに置き換えることが可能であるはずだという強い確信がヒルベルトにはあった。

そしてそこにはおそらく、『原論』の呪縛から逃れたいという欲求もあったはずだ。

それはまた、古代ギリシャの呪縛から逃れるということでもある。

ここでいう記号的、というのはつまり、離散的ということでもある。

離散的というのはつまりレゴブロック的で、連続的というのは粘土的ということだ。

広い意味でのビットマップ画像は離散的で、ベジェ曲線は連続的だ。

「記号的」であるにも関わらず連続的なものもある。

以下は『魔法陣グルグル』で示された例である。

あまり伏せた意味がないかもしれないが、一部セリフを伏せたのは最初のボス戦のネタバレになるかもしれないからである。

単純に図形を伝えているのであれば、トポロジー的に離散的な記号に置き換えることはできそうではある。

ただ、この作品では、単純にそうともいえないことが示唆されている。

それはともかく、ブルバキはいつまでも形式バカだったわけではなく、その姿勢も変化し、その変化が他の数学者へも影響した。

『ヒルベルトの挑戦』P.242には以下のようにある。

いかに正しい証明を書く際に重要であろうとも、論理的な形式主義は数学のなかでまさしくいちばん退屈なものだ、という見方をブルバキはするようになった。それよりも、「まさに、論理的な形式主義だけでは与えることができないもの、つまりは、数学の奥底に潜む明瞭性」こそが最も重要な目標だとみなした。この見解に影響されて、数学者の考え方全般が新しく変化することとなる。数学者は当然ながら、数学には意味があると信じている。愚かな教師に支配された学生とはちがい、次々と証明を出すことがなによりも重要だとは考えていない。数学者が互いの研究において最大の敬意を払うのは、なんらかの発見がなされているか、新たな結果が以前からある結果にいかにぴたりと当てはまりそれを説明づけているか、という点である。ただ単なる証明よりも、説明のある議論のほうが好まれる。そのほうが応用がきき、したがっていっそう強力だからだ。ブルバキの新しい目のつけどころは、理論と理論がどう整合するかに光を当て、その過程を容易にする公理的な定式化を選び出すというやり方にあった。

このように見ると、21世紀に入ってからのブルバキ批判の中にも、初期のブルバキを否定してはいるが、結局のところ批判者の立場が後期のブルバキをなぞるものであるといえるようなものである場合がある。

いま日本では岡潔ブームだそうだが、岡潔はあまりにも独創的だったのでブルバキのような複数人のユニットなのではないかと疑われた。

岡潔をスターにしたのはブルバキの面々、特にカルタンだったが、岡潔がカルタンのことをどう思っていたのかはよく分からない。

『怠け数学者の記』には、プリンストン高等研究所にいたころの小平邦彦が妻に宛てた手紙が掲載されている。その1950年2月5日のところには、以下のようにある。

ニューヨークで関西配電の重役に会いました。この人が岡潔氏と同級であったそうで、岡さんの話をいろいろしていました。フランスの数学の長老アンリ・カルタン (H. Cartan) から招待状が来たのに「カルタンにおれの数学が分かるものか」と言って紙屑籠へ投込んでしまった、というような話でした。岡さんはこちらでは非常に有名で皆に「岡はどうしているか？」と聞かれます。日本では今まであまり認められなくて気の毒です。

岡潔とカルタンのエピソードについては、どちらかというと2人の関係を美化したものがよく紹介されている。

ちなみに上記の「カルタンにおれの数学が分かるものか」発言のソースはずっと探していたのだが、途方もない紆余曲折のすえ、俺の友人が2018年9月になってから見つけてくれた。

でも岡潔も、いつもいつもカルタンのことをこんな風に思っていたわけではないのかもしれない。岡潔は日によってまったく気分が違っていて、現代的な言い方で言ういわゆるラピッドサイクラーなのかどうかは不明だが、それなりに病的なレベルだったらしい。

あまり岡潔の発言に一喜一憂しないほうがよさそうではある。

ちなみに岡潔はポアンカレを高く評価していた。

ところでブルバキは、ヒルベルトがもたらしたものの「継承者」としてとらえられることが多いわけだが、それはどういう風に「継承者」なのだろうか。

『数学の天才と悪魔たち』P.53には以下のようにある。

楽天家と傲慢の学問的側面としてヴェイユはじめブルバキ一派は、徹頭徹尾、数学のメタ的考察を無視してきたことが指摘できる。だから彼らはヒルベルトの半分の弟子に過ぎない。

つまり、ブルバキの仕事はヒルベルトを特権的な他者としてとりあつかうことによって成り立っていた。

ヒルベルトの前にひれ伏すのではなく、ヒルベルトの隣に座ってヒルベルトがしたように数学をメタ的に考察するなら、それは結局、ヒルベルトとは違う形で数学をとらえることになるかもしれないのである。

そういう意味では、ヒルベルトの隣に座っていたのは、信奉者たちではなく敵対者のポアンカレだ。

ヒルベルトとポアンカレの感覚的な違いを理解するうえで重要なのは、ポアンカレは幾何学的な直感をあくまでも重視していた。

ポアンカレは単に保守的に『原論』のような捉え方を守ろうとしたわけではなく、体感的な世界の捉え方自体が独特だったのではないかともいわれる。

ところでヒルベルトがもたらした大きな問題提起の一つに、「無矛盾なら存在する、だから無矛盾であることを証明せよ」がある。

この「無矛盾なら存在する」についても、ヒルベルトの天才的ひらめきによるものではない。

そもそも、基礎論のもう一人のスーパースターのカントールが、1883年の『一般多様体論の基礎』の中で以下のように主張している。

数学の諸概念は無矛盾でなければならないが, 同時に先に与えられた概念との関係が確定的に区別できるように与えられていさえすれば, 数学においてはその概念は存在しており, 実在的であるとみなせる.

訳は『フレーゲ・デデキント・ペアノを読む』P.141より。

存在とは何かというのはまさに神学的な議論だ。

当時の感覚なら、19世紀前半の非ユークリッド幾何学によって、「我々は多神教的世界に迷い込んでしまった」と感じていた人も多かっただろう。

ヒルベルトがどう思っていたかはともかく、『原論』の呪縛から逃れるということと、古代ギリシャの多神教から完全に脱却して唯一神の存在が証明されてほしいという願望を結びつけていた人もいたかもしれない。

19世紀後半のドイツにおける存在をめぐる議論は、例え数学者が書いたものであっても、唯一神が全知全能であるということを前提に書かれているわけで、そこを無視するとまったく捉え方が変わってしまう。

数学者本人に信仰心があるかどうかは、あまり関係がない。当時のドイツで無神論者であることを表明するのは、2018年現在の日本で「オーストラリアは実在しない。イギリスのでっちあげ」と主張するようなものだったからだ。

今の日本やアメリカとは、まさに「社会通念」がまったく違っていたわけだ。

カントールと対立して数学史上最大の悪役といえる存在になったクロネッカーの有名な言葉に、「神は整数を作った。残りはすべて人間の仕業だ」というのがある。

クロネッカーは必ずしも旧態依然とした考えを守ろうとしていたわけではなく、カントール達とは別の「革命」を志向していた。

しかもクロネッカーはユダヤ系だった。

カントールやフレーゲやデデキントやヒルベルトがドイツ、ペアノがイタリア、ニュートンがイギリス、ポアンカレがフランス。

その後に起こったことを考えると「何も連想するな」という方が無理な話である。

それはともかく、数学基礎論の勃興に大きな影響を与えた著作に、チェコの神学者ベルナルト・ボルツァーノによる『無限の逆説』(1848年完成) がある。

ボルツァーノはプラハ大学で宗教哲学の講義をしていたが、危険視されて大学を追放された。

ドイツ語で書かれたこの『無限の逆説』に、「無矛盾なら存在する」の原型となる発想がある。

時系列で重要人物たちの発想を要約してみる。

ボルツァーノ「人間の認識を超越して、客観的に存在するものがある。新しい命題を作り続けることができるなら、それは存在する」

↓

ハンケル「論理的に可能で、自己矛盾しないなら、実在性を気にする必要がない」

↓

カントール「無矛盾であると同時に、先に定義したものと確定的に区別さえできれば、それは存在する」

↓

ヒルベルト「形式的なシステムの中で無矛盾なら、それは存在する」

ハンケルはどちらかというと、「実在」についてムキになるのはバカバカしい、なぜ整数が実在するなんて無邪気に信じられるんだ？という感覚があったのかもしれない。

世紀末における様々なパラドックスの発見により「無矛盾」を形式化によってはっきりさせようという機運が徐々に前面に出てきた、という時代の背景はあるものの、基本的にはボルツァーノの考えを言い換えただけともいえる。

ヒルベルトの場合は、特定の数学的対象の実在だけでなく、「数学全体」を強く意識していた。

数学の中で数学が無矛盾であることを証明することによって、数学の実在性を証明しようとした、ともいえる。

巧みな形式化によって数学全体を「解決」するという発想も、ヒルベルトではなくライプニッツが源流とされる。

ヒルベルトの功績は、一部のヒマ人の夢想に過ぎなかった問題を、魅力的な数学の問題として定義し直し、これらを解くことがいかに今後の数学にとって重要かを説いて感化したことだ。

そしておなじみの話として、「無矛盾」の夢はゲーデルによって砕かれるわけである。

ヒルベルトの夢は砕かれたものの、この時の形式化についての議論がコンピュータの基本原理やプログラミング言語に大きな影響を与えた。

そしてもちろん、そのコンピュータの上に数学を乗せる、ということも行われている。

場合によっては、コンピュータで証明の正しさを判定することだってできる。

ただし、単に形式化さえされていればいいわけではない。

それが厳密に形式的に記述された証明で、間違いがないことがコンピュータによって自動的に確かめられるような場合であっても、ある大きな問題がある。

例えば背理法を使っていた場合だ。

『無限のスーパーレッスン』P.108には、以下のようにある。

都合上ラッセルの集合についてもそのまま引用するが、意味を理解している必要はない。ラッセルの集合がパラドックスを起こすということだけを意識していればいい。

「存在そのものが、矛盾。かっこええですなあ」

「ラッセルにとっては、かっこいいどころではありません。背理法、という論法をこのレッスンでも一度使いましたが、覚えてらっしゃいますか？ Aという仮定をおいて議論を進めていくと、矛盾が起こる。したがってAは正しくない。そんな証明方法でした (56ページあたり参照)」

(中略)

「小さなほころびどころではありません。ラッセルのパラドックスを使うと、何でも証明できてしまいます」

「どうゆうことです？」

「たとえば、1=2を証明したいと思ったとしましょう」

「そんなん、証明できるわけありませんやん」

「まあまあ。1=2でなかったと仮定しましょう」

「仮定するも何も、現に1=2やあらへんやないですか」

「背理法を用いると、この時に、つまり1=2でないと仮定した時に、何か矛盾が起こりさえすれば、1=2でない、と仮定したことがおかしい、ということになります。さて、1とか2とかはともかく、ラッセルの集合Sを取りましょう。SがS自身に含まれていると仮定しても矛盾が起こるし、SがS自身に含まれていないと仮定しても矛盾が起こります。この矛盾の原因は、1=2ではない、と仮定したのがおかしかったので、実は1=2が成り立つことがわかりました」

「ちょっと待ったあ！ ラッセルの集合Sと、1=2と、何の関係もあらへんやないですか」

「関係があるかどうかはともかく、今のは背理法にのっとった厳密な証明ですよ。1=2でないと仮定して、色々議論を進めると矛盾が起こる、よって1=2である、と。今のはわざと関係がないことがはっきりわかるように、こういう議論にしたんですが、じゃあ、Sに関係する話だったら構わないわけですか？ 何か自分自身を含まない集合の話をしていて、自然にラッセルの集合Sが出てきて、Sを考えたら矛盾するから、背理法で証明終了、とか言われたら、それは構わない、というわけですか？」

「そ、それはちょっと……」

「本来全然関係のない話でも、どんどん話を広げていって、うまくラッセルのパラドックスに話をつなげていって、それで矛盾したから背理法で証明完成、とか言われた時に、その証明そのものは、論理的に間違っているわけじゃないから、反論ができないんです」

「(56ページあたり参照)」は書籍にもとからあった記述で、「(中略)」は俺が挿入したものである。

論理的に間違っているわけではなく、厳密に形式的に記述された証明であっても、数学的に無効なものである場合がありうるということである。

これは人工知能が、非常に長大でしかも全体のビジョンや部分に分割して考えるためのガイドラインもないような証明を「出力」したりした時にも十分注意する必要があるということでもある。

今でも数学の証明の正しさは人間がチェックしている。

有名な問題が証明された時、数学の証明なのに正しさを確認するのに何でそんなに時間がかかるのか、と疑問が発せられることがある。

これは「数学なのに」ではなく「数学だから」とでもいうべき事情があるのである。

またそもそも、形式化によって自動的に正しさを判定するとしても、「この形式化のあり方は正しい」と判定するのはやはり人間である。形式化のあり方が間違っていれば、元も子もない。

こういう条件さえ満たしていればその形式化システム群はすべて正しい、というように形式化のあり方の正しさを自動判定できるようにしたとしても、その「こういう条件さえ」の部分が正しいのかはやはり人間がチェックするのである。

さらに、その「こういう条件さえ」の部分の正しさ判定を自動化したしても、さらにその背後には人間がチェックせざるをえない何かがある……というわけで、これは無限に後退していくのである。

人類は今となっては1900年前後のヨーロッパでの議論はすっかり忘れて、コンピュータは日常に浸透した。その強力な実用性によって。

ビットコインなどのブロックチェーンも、コンピュータが世界中に広く浸透して、相互接続されている状態が当たり前だから成立している。

当時のドイツでの基礎論の盛り上がりは、今だから冷静に分析できるわけだが、当時は様々な批判があった。

ポアンカレはカントールについて、事実上の全否定を行っている。

これは心理学にとって興味のあることかもしれないが、これは定理ではない。それは1つの状況にすぎない

訳は志賀浩二著『無限への飛翔』P.78より。

これは天才が天才を見抜けるとは限らないという印象的な例だ。

また、以下のような「予言」もしている。

のちの世代は [カントルの] 集合論を、もうそれからすっかり回復した一種の病気とみなすだろう

訳は『数学10大論争』P.287より。

ただし、ポアンカレも1908年の講演では、必ずしも否定的ではない形でカントールの集合論に言及したようだ。

1854年生まれのポアンカレはその講演の4年後の1912年に58歳で死亡する。つまり、ラッセルの『プリンキピア・マテマティカ』の第3巻が出る前に死んだ。

ポアンカレと論争を展開した1872年生まれのラッセルは、1910年から1913年にかけて『プリンキピア・マテマティカ』を刊行し、1930年代のゲーデルの不完全性定理も目撃し、第二次世界大戦も目撃し、アインシュタインと共に反核運動も展開し、1970年まで生きることになる。

カントールも1910年代に死んでいるしヒルベルトも第二次大戦中に死んでいる。ヒルベルトは本気で生きている間に数学全体を「終わらせる」つもりだったかもしれないが、数学基礎論の立役者たちが結果的に逃げ切るような形になったのに対し、ラッセルはいろんな意味で逃げ切ることを許されなかった存在だ。

ゲーデルの証明が持つインパクトも、十分に浸透したのは第二次大戦後で、レイモンド・スマリヤンによる解釈の影響が大きい。

ゲーデルは証明の中で人工言語を設定し、ラッセルやブルバキのように律儀に展開していくのではなく、曲芸的な技巧によって特殊な命題を構成してみせた。

だから20世紀の最初のスーパーハッカーはゲーデルだ。

ところで、基礎論のスターたちと対立した数学者の中で、こういう話題についてポアンカレよりもっと尖った発想をしていた人がいる。ブラウワーだ。

『フレーゲ・デデキント・ペアノを読む』P.143に、ブラウワーの思想が要約してある。いくつか抜粋してみよう。

(5) 数学は言語的に表現される理論でもなければ, また何か客観的な実在に関する抽象的な真理の集積でもなく, むしろ人間精神の行動, あるいは創造である.

(9) 言語的表現は数学に本質的なものではなく, 数学的構成の精神的過程を個人的記憶として留めておくための補助手段である. 言語は意思を通じるための不完全な道具にすぎないから, 相手に望むような構成を辿らせるのに成功しないかもしれない.

(10) 証明とは数学的構成 (建造) を実行することである. 数学にとって絶対的に安全な言語は存在しないので, 論理主義者や形式主義者が考えるように, 証明を命題の論理的な関係の列と見ることはできない.

(13) 論理学は一種の応用数学である. 論理は数学の基礎に依存するが, 逆ではない.

(14) 数学の構成は永遠に固定されているということはなく, 自由に成長し, 人間の経験とともに変化していく. 形式的体系は, 静的なため, 創造的な数学的活動の開いたダイナミックな領域を把握することは不可能である.

もちろんブラウワーの時代にはコンピュータが無かったが、あるいは無かったからこそ示唆的で予言的である。

特に、「言語は意思を通じるための不完全な道具にすぎないから、相手に望むような構成を辿らせるのに成功しないかもしれない」の部分。

プログラミング言語のコードを書くとき、人間に向けて書いている部分とコンピュータに向けて書いている部分が複雑に絡み合う。

コメントの部分を除外したとしても、そうなのである。

そして人間に対してもコンピュータに対しても、「相手に望むような構成を辿らせるのに」失敗することがある。

「論理学は一種の応用数学」の部分は、一見するとブラウワーが間違っていたようにもみえる。

現代のほとんどコンピュータはCPUが積まれていて、CPUが基礎にしているのは論理演算だ。

C言語などのプログラミング言語をコンパイルするということは、自分の書いたコードを論理演算で構成し直すようなものだともいえる。

今のコンピュータ環境で起こっていることは、論理学で基礎づけたうえにすべてを構築していることになる。

でもだからといって、数学が論理に依存しているのが確定したわけではない。

現代においても、数学者による数学的営みのほとんどは、論理学の基礎づけを意識しているわけではない。

そしてなんと言っても、「数学の構成は永遠に固定されているということはな」いという部分。

ある種の定理や証明をコンピュータの上に乗せることができるようになったとはいっても、数学者による数学的営みのすべてを、形式的な言語に置き換えることはできない。

数学が不変の土台の上にあるというのはまったくの幻想だ。土台に目を向けると、とたんにすべてがあやふやになる。

好みや根拠のない断定や個人的崇拝などによって「支えられている」。

土台があるのではなく、ただ、無限の大きさを持つ巨大なスクリーンがある。

そのスクリーンには、量的に距離を縮めるということができない。

量的に近づこうとするからだめなのだ、構造的に、一気に手中に収めるようにすれば、と考えても、それもやはりかなわない。

それは量的にも、構造的にも、永遠にすり抜け続ける。

最近よく、プログラムを静的なものとみなすか動的なものとみなすかという議論がある。

これは実際には、ヒルベルトとブラウワーの対立の再燃なのである。

俺は、プログラムは「よりセキュア」という状態はあると思っている。

「セキュア」か「notセキュア」かのどちらかしかない、というのは、コードを静的なものとして捉えている。

変数名を「テーブル」や「椅子」に変更しても、コードを静的とみなせばセキュアかどうかは変わらない。でも、コードを動的に捉えれば、分かりやすい変数名にしたほうが、よりセキュアである。

どんなコードも変更される可能性がある。別の人が変更する可能性もある。

よく「コメントは未来の自分のために書け」と言われるのも、今の自分と数年後の自分が完全に「同一」ではないことを前提にしているのだといえる。

直接的・短期的にはコンピュータの動作に影響がなくても、「同一」でない誰かによって変更されることを前提にしていれば、読みやすいほうがより安全である。

読みやすいことによって、あとから誰かが穴を追加する確率が減るからである。

「同一」の問題は、人間の側だけでなく、コンピュータの側にもある。

この記事の最初のほうで、同じSchemeの実装系のGaucheとGuileでの実行結果の違いを示したが、もっと単純に、言語のバージョンアップという問題がある。

これはブロックチェーンのスマートコントラクトにおいても重要だ。

ある時にチェーンに乗せたコードが、いざ実行される時が来たという時になって、言語のバージョンアップによって意図しない動作をされては困るからだ。

イーサリアムのスマートコントラクトのための言語Solidityでは、「このコードはSolidityのこのバージョンで解釈してください」と宣言することができる。

Solidityのバージョンアップによって、同じコードがまったく違う意味になるのを防ぐためである。

でも将来のイーサリアムで、本当に今書いたコードが意図通りに動作するのかは、現時点では誰も分からない。

コードがコードであるためには、様々な暗黙の前提が必要である。状況によってコードがどのような意味を持つのかは変化する。

コードを動かすための実装系も動的な存在だし、その実装系が動くハードウェアも動的な存在だ。

石田彰が演じるアニメキャラ達のように、さんざん思わせぶりなことを言ったあげくに責任を取らずに退場していった感のあるブラウワーだが、ブロックチェーン革命、AI革命、IoT革命、と騒がれる昨今において、あらためて彼の発言についてじっくり考えてみる必要がある。

ところで、デジタルデータは簡単にコピーできるが、人工知能が意識を持った時、システムをまるごとコピーしたらどうなるのだろうか。

いやそもそも、AIが意識を持ったりするのだろうか。

ゲーデルの証明は、理性の限界を示したなどと言われたために、意識の問題と結び付けられることがある。

でもこれは、当時の世界最高峰の知性の持ち主たちがヒルベルトの計画について「これでいけるんじゃないか」と思っていたという状況も含めて、「理性の限界」という発想が広がったと考えたほうがいい。

ゲーデルの証明によって人間の思考の限界が示されたわけではなく、あくまでも形式的記述の限界が示されただけである。

みんな大好き『ゲーデル・エッシャー・バッハ』の20周年記念版 (日本語訳は2005年刊) では、20年前のオリジナル版は「現在の僕とは全く別人の」、「ひとりの若者の作品」だから誤植も直さない形で出版された。

でもここで序文が追加された。

この序文では、意識について書かれている。これはペンローズを念頭に置いているのは明らかだ。

ペンローズの意識についての議論は、確かに根拠が薄い。

でも、それをいうなら、ダグラス・ホフスタッターのいうように、本当にパターンそのものが意識をつくるのかどうかも、やはり根拠が薄い。

これは両方とも根拠が薄いというだけで、ブラウワーの議論によってペンローズの考えが補強されるというわけではない。

一つ確かなのは、他者が意識を持っているのかどうかは、永遠に確認できないということである。

もしあなたが意識を持っているなら、同じように意識を持っている存在が無数にいるのか、それともこの世界で意識を持っているのは実はあなただけで他のすべては紙芝居のようなものにすぎないのかどうか、ということは、いかなる手段を持っても確認できない。

もし時代が進んで意識を融合することができたとしても、融合する相手に本当に融合するまで意識があったのかどうかは、分からない。「意識があった」という「記憶」が現在において存在するということしか確認できない。その記憶だって、融合のショックで記憶が捏造されたりしていないかどうかということも分からない。

これは単に、意識の性質をあらわしたものではないかもしれない。

部分と全体が同じであることを無限の定義として利用することが無限史におけるコペルニクス的転換だったように、他者の意識を確認できないことこそ、意識を定義するものかもしれないのである。

あなたが意識を持っているなら、あなたがあなたであり続けることからは、逃れられない。

どのような変化があっても、あなたはあなただ。

では、意識を持たない存在はどうだろうか。

例えば、特定のブロックチェーン。

いや正確には、ブロックチェーンが意識を持っているのか持っていないのかは、いかなる手段をもっても確認できない。

今となっては、ビットコインやイーサリアムは巨大になりすぎたともいわれる。

巨大なブロックチェーンたちは今後どのように変化するのだろうか。

巨大すぎて、下手に変えると大変なことになるという懸念もある。

Too Big To Fail (大きすぎて潰せない、大きすぎて失敗させられない) である。

そうは言っても、Too Big To Keep The Status Quo (大きすぎて現状維持できない) ということもまた、あるのかもしれない。

・2018-10-28 21:05 記事を一部訂正

修正前「./code10b.rb '7'」

修正後「./code16.rb '7'」