

当たりを引く確率が1/pのくじaを考える(p≧1)
まず純粋に1回引いて当たりを引く確率は1/p ...(1)
次にくじaの当たりをn倍したくじAを考える(n≧1)
このくじを1回引いて当たりを引く確率はn/p ...(2)
次にくじaと同じものをn人に分け、n人がそれぞれ同時に1回引いたとき、少なくとも1人が当たりを引く確率は 1-{(p-1)/p}^n ...(3)
(p-1)/p ... 当たりを引かない確率
↑をn人分繰り返し、その補集合を取った
n/pと1-{(p-1)/p}^nについて
1-{(p-1)/p}^n
=1-(1-1/p)^n ...(3)'
(1-1/p)^n
=1-n/p+{n(n-1)/2!}p^2-{n(n-1)(n-2)/3!}p^3+...
(3)'は変形でき
1-(1-1/p)^n = n/p-X...(4)
X={n(n-1)/2!}p^2-{n(n-1)(n-2)/3!}p^3+{n(n-1)(n-2)(n-3)/4!}p^4... (5)
X={n(n-1)/2!}p^2-{n(n-1)(n-2)/3!}p^3+{n(n-1)(n-2)(n-3)/4!}p^4......≧0のとき、(2)≧(3)となる。
1-(1-1/p)^n=n/p-X
X=(1-1/p)^n+(n/p-1)
X≧0のとき
(1-1/p)^n≧1-n/p
(1-1/p)^n-(1-n/p)≧0
f(n, p)=(1-1/p)^n-(1-n/p) とおく
pで微分
fp(n, p) = -(1/p^2)n(1-1/p)^(n-1)-n/p^2
1/p^2 > 0, n≧1, (1-1/p)^(n-1)>0 なので
fp(n, p) < 0
p=1...fp(n, 1)=-n < 0
lim(p→∞) fp(n, p)=0
また
lim(p→∞) f(n, p)=0
p=1...f(n, p)=n-1≧0
つまりf(n, p)はpについて1から大きくさせていくと減少し続けるが、どれだけpを大きくしても(∞にしても)0である.
つまりpについて変化していってもf(n, p)≧0
nで微分
fn(n, p)=log(n) (1-1/p)^n+1
log(n)>0, (1-1/p)>0 なので
fn(n, p)>0
n=1...f(n, p)=0
つまりf(n, p)はnについて1から大きくしていくと増加し続け、また始めの値は0である。
つまりnについて変化していってもf(n, p)≧0
よってf(n, p)=(1-1/p)^n-(1-n/p)≧0
(1-1/p)^n≧(1-n/p)
(2)≧(3)となり、n人がそれぞれの箱から1回ずつ引くよりもn倍当たりやすい1つの箱を使ったほうが当選しやすい。
投稿者の人気記事




コインチェックに上場が決まったEnjin Coin(エンジンコイン)コインを解説

Uniswap v3を完全に理解した

ジョークコインとして出発したDogecoin(ドージコイン)の誕生から現在まで。注目される非証券性🐶

Polygon(Matic)で、よく使うサイト(DeFi,Dapps)をまとめてみた

【第8回】あの仮想通貨はいま「テレグラム-TON/Gram」
Uniswap(ユニスワップ)で$ALISのイールドファーミング(流動性提供)してみた

約2年間ブロックチェ-ンゲームをして

CoinList(コインリスト)の登録方法

NFT解体新書・デジタルデータをNFTで販売するときのすべて【実証実験・共有レポート】
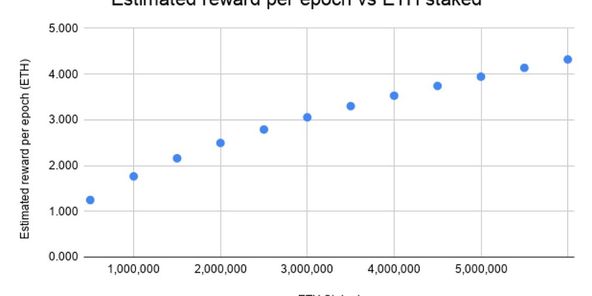
Eth2.0のステークによるDeFiへの影響を考える。

2021年1月以降バイナンスに上場した銘柄を140文字以内でざっくりレビュー(Twitter向け情報まとめ)
