生きるアルゴリズム：05

Baye's rule：世界を正しく見る

ベイズの定理というのを聞いたことがあるでしょうか、僕も聞いたことはあるし数式を見たことはあります、高校数学や大学数学の初めに出てくるような数式だと思います。彼の定理の中で特に大事なのが事前確立というものです。

例えば、当たる確率が全く分からないくじを引いたとします、くじからでるのは「あたり」か「はずれ」のいずれかです。もしあなたが一回引いてあたりを出した場合、あなたはくじの中からあたりが出てくる確率をどう予想するべきでしょう？ここに注目したのがベイズとそれより少し後に出てくるラプラスという人です。

ラプラスは数学的にこういった場合、つまり

全く事前情報がない状態で結果としてAかBのいずれかが出る試行W回行いそのうちN回Aが出た、というときにこの試行でAが出る確率として最適な推定値

が(N+1)/(W+2)であることを証明します。

しかし、現実世界ではあまりこういった状況はありません、むしろ多くの場合何かの手立てをもとに事前確立の分布を予測できることが多いです。

例えば寿命ですが、これはいわゆる正規分布することが知られています。正規分布は以下のような分布をしています。真ん中に来る頻度が一番高く端に行くと頻度が小さくなっていきます。

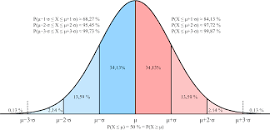
寿命を例にとると80~85くらいが寿命の人が多いけど10歳や120歳は少ないというような感じですね。

こういったグラフにおいて個人の未来を予測するとき、平均の法則を利用します。つまり、生まれてからの年数分左端の確立が減るのでその分だけ予測をみぎにずらします。例えば6歳児は84歳くらいが寿命だと予測し、90歳の人は94歳くらいだと予測します。あくまで平均周辺に収まることが多いことを前提にした予測になります。

他にも現実でよくある確率分布にはアメリカの年収のような左に多くの人がいて、右のほうにしっぽが長く伸びたようなグラフもあります。

有名な話ですが人口の99%人の収入が平均収入を超えず、代わりに上位1%は平均の10倍稼ぎ、さらにそのうち上位1%はその10倍も稼ぐというような形ですね。

こういった事前確立からの予測は乗算の法則にしたがいます、富める人ほど見込み収入が大きくなっていくというような感じです。SNSなんかいい例だと思いますが有名な人がさらに有名になる確率は無名の人が有名になるより大きいということです。

もう一つ日常的な事前分布として、上の2分布の間の形をした分布としてアーラン分布があります、しばしば待ち時間分布と称されます。この分布から予測を行うときは加算の法則にのっとります。どんな事前情報が与えられても一定の値が加算されて帰ってきます。例えばあるかけ事が好きな人がカジノに行きその妻が帰りを待つとします。夫はブラックジャックをプレイしてもしブラックジャックが出たら帰るといっているとします、そうすると出かけた時点で夫の帰ってくるまでの時間の期待値はゲーム一回にかかる時間×20倍（ブラックジャックの出る確率は1/20なので）です。妻は夫が1時間たっても帰ってこないので心配してカジノに迎えに行きました、夫はまだブラックジャックを出せていません、この時夫が帰れるようになるまでの時間の期待値はいくらでしょう？さっきと全く変わりませんね。

こういった事前分布の変化によって予測値は変わってくるので例えば○○という病気の平均余命は○○年というのもその裏にある分布をみてみるまで、その患者がどのような予後を典型的にたどるのかはわからないということです。

ちなみに、人間の直感というのはすごくて身の回りの経験則から僕らがはじき出す様々な事柄の予測値はかなりベイズの定理を利用した予測値に近いことが知られています。だからこそ直感的にも今お金持ちの人は次の月の収入も一般人より多いという感覚や、10歳の子は80歳の老人よりこれから生きる時間が長いという感覚はわかるものなのです。

しかし、そのかわり自分たちの身近にない（つまり事前確立があまり直感的にわからないものに関しての予測はめっぽう弱いです）、例えばエジプト王朝って何年続いたでしょうと言った問題への回答はバラバラな傾向にあります。

人間が直感的に正しい予測をするには正しく世界を見る（事前確立を把握する）必要があります、しかし、人間は自ら生み出した言葉や技術によってこの事前確立を乱しています。人から聞くことはその人が面白いと思ったことや自分にとって興味がある事である確率が高まります、完全にニュートラルな入力ではないために僕たちの世界の認識は少し、ゆがみます。同じように報道の偏りもそうです、おそらく多くの人は飛行機事故の死者数と自動車事故の死者数の比を本当の比より近いと予測します。これは飛行機の自己のほうがメディアに取り上げられやすいというバイアスによります。ツイッターを例にとれば同じ分野のフォロワーが多いわけですから自分の分野が盛り上がってるように見れるかもしれませんね、本当は全くそんなことなくても。

自分の直感を正しい状態に保っておくためにはSNSやメディアから距離を取るのもいい方法なのかもしれません。