

◇序

本当は自分で作りたいものがあった。
風の音を聴きながら、それがオリエンタルな響きを伴って、自分自身を新たな感覚の世界へ旅立たせてくれるとしたら。
アイデアはそこにある。作ってみたら発表するのもいいかも、とか考えたりした。しかし、自分はどうも面倒風が吹きやすい。今回、Python に可能性を見いだせてなかったなら、公表すらしなかっただろう。
それは音楽だろうか?
少なくとも、自動で音を奏でるプログラムとは言えそうだ。
それは創作的といえるだろうか?
それは分からない。なにしろ、まだ作ってないのだから。
今回は、オリエンタル・ウインド・チャイムの設計書と題して色々書いてみる。少し早いが、春休みの工作?にはちょうどいいかもしれない。
◇目次
全体の容量が大きくはないが、すべてを確認するのに20分程度かかるので目次を表す。全体をコンパクトにするため、「おまけ」はない。
<オリエンタル・ウインド・チャイムの設計書2>
◇序
◇目次
◇継承
◆SimpleAudio.py の使用
◆FM 音源の作成
◆使用モードの確認
◆変更強度やリズムの設定
◆ミックス時の注意点
◆その他
◆今後の予定
---(おまけは、ありません)---
◇おまけ1 じゃん…
◇おまけ2 けん…
◇おまけ3 グー✊!!
◇継承
お気づきか、お気づきでないかは存じ上げないが、これは以下の記事の継承である。
まあ、おおよそ面倒風が吹いたか、はたまた長さだけの仮説に限界があったところだろう。その弁明というか、弁解というか、だいたい人間性のあらわれるところにして、それではプログラムでやってみよう、というものである。
GUI はモチベーションとしては強いが、扱うのはいろいろ面倒なところがあるので、それは今後の予定として、今回は音の部分だけを製作してみた。
とは言いながらも、FM 音源のいろいろなパラメータを想定したものもあったり、ランダムに鳴らしながらなるべく音楽的にするなど、工夫自体は大きいものになった。が、手続き的構成やロングスパゲッティなどのコード部分や、リズムや変化あるいは再現性など音楽面の部分は、まだまだ改善できると思われる。
◆SimpleAudio.py の使用
まずサウンドだが、今回は SimpleAudio.py を使用することにした。
他に、PySound や PyGame という選択肢もあったが、データを再生したいことや、のちのちPySimpleGUI を使用したいという想いもあったので、今回はこれにした。
サウンドを読み込む場合は、圧縮系がいくつか直接読み込めないので注意が必要だ。ただし今回は、波形を別ファイルにして出力する計画も、読み込む計画もないので、フォーマット変更のためのさらなる追加ライブラリは必要ないだろう。まあ、必要があるとすれば、自分の頭の中の妄想を圧縮するソフトくらいだろう。
今回は…今回も、流しの手続き型なので、上から順番にコードを表示する。
import math
import matplotlib.pyplot as plt
import numpy as np
import random
import simpleaudio as sa
PI = np.pinumpy がある時点で math はいらない気もするが、まあいいだろう。matplotlib はできた感を演出するための飾りであるが、のちのち必要になる可能性は高いと考えている。M字男が、FFT(ファースト・フーリエ・トランスフォーム)という FF(ファイナル・フラッシュ🎆)に似た必殺技を繰り出してくるおそれがあるので、ちゃんと避けられるよう準備しておかなけらばならない。
余談だが、& も日本語もないので、シンタックス・ハイライトというもので表示できる。UTF-8 の表記をすれば、使えたりするのだろうか…
◆FM 音源の作成
FM 音源はベル系、金属系の音が得意だ。「ウインド・チャイム」という名前のとおり、金属的で変化の大きな響きが要求されている場合はとくにぴったりだ。
ところで、元来の FM 音源というのはウェーブ・テーブル・シンセというのが正しい。純粋にサイン計算を行って値を返すのではなく、サインテーブルというデータ(メモリ)をあらかじめ用意しておいて、読み出し時にデータのアドレスをタイムに従って増やしながら、前後にプラスマイナスつまり変調して出力するものである。更にはその出力をアドレスに見立てサインテーブルに…と段数をあげるものである。
したがって、同様のデータテーブルであれば実のところ、定数域に収まればなんでも構わないということになる。意味があるかは分からないが、仮想通貨アドレスでもできることになる。まあ、5秒後に A ボタンの効くストリートファイターⅡをやりたいか?、と聞かれた時と同じような答えになるだろう。
少ないメモリや計算能力で処理できたために、古くから存在していた FM 音源で、いっときは下火であったが、最近はまたブームを戻している感はある。まあ、とかなんとか、うんちくはもういいだろう。以下は、うんちくよりひどいスパゲッティーである。
hz = 440
rate = 44100
fm = 50
ratio = 2 - 0.005
noise = 0.4
sine_wave = [math.sin(x*hz*PI*2/rate) for x in range(rate)]
fm_wave = [[math.sin((x+
math.sin((x+
math.sin((x+
math.sin(x*(hz*(2**(i/12)))*PI*2*(ratio*ratio*ratio*ratio-1)/rate)
*fm*1.4/1000*rate/(hz*(2**(i/12)))*((rate-x+1)**3)/(rate**3)
+random.random()*PI*2*noise)
*(hz*(2**(i/12)))*PI*2*ratio*(ratio+0.5)/rate)
*fm*1.2/1000*rate/(hz*(2**(i/12)))*((rate-x+1)**2)/(rate**2))
*(hz*(2**(i/12)))*PI*2*ratio/rate)
*fm*1.1/1000*rate/(hz*(2**(i/12)))*(rate-x+1)/rate)
*(hz*(2**(i/12)))*PI*2/rate)*(rate-x+1)/rate
for x in range(rate)] for i in range(0, 37)]
disp_wave = fm_wave[0]
fm_wave = [np.multiply(fm_wave[i], 1/(5+(i/3))) for i in range(0, 37)]
print('Make sound file!')
sine_wave は、内包表記を使用している。これはただのコピペなので信頼できる。
次の fm_wave で、FM 音を3オクターブ分まとめて作っている。本当は、ひとつずつレイヤーや変調をかけていたのだが、音を聴くのが面白くなって、気づいたらもはや取り返しのつかないSS (スーパースパゲッティー)ができた。次の disp_wave までが一文であり、そして二重の内包表記になった。まあそれでも、BrainFuck や WhiteSpace に比べればまだまだましな方だろう。
FM は基本的には、Sin((x+a*Sin(b*x*Pi*2))*Pi*2) を押さえておけばなんとかなる。が、上記は些少説明が必要だろう。
まず、ratio が出てくるところで変調元の周波数を変えている。基本的に、変調元に近いほど高くしている。-0.5 は低音を付加している。また、ratio = 2 -0.005 の小数部分はデチューンである。EFX でいうコーラス効果がある。
((rate-x+1)**3)/(rate**3) のような式は、ADSR でいうところのディケイである。変調元ほど、早く減衰するようにしている。
fm が出てくるところは変調効果の強さを決めている。変調元ほど刺激的なほうが、金属音を作る場合には都合がいい。
random*noise でノイズを付加している。変調元にノイズを付加すると、倍音に豊かさが生まれる。EFX でいうところのサッチュレータだ。ここでサッチを思い浮かべる人間は、危ない系ギタリストだ。
あとの、disp_wave は matplot 用で、その後もう一度 fm_wave を再代入したのは、ミックスするのにどのみち音量を下げる必要があるからだ。ステレオを変化したい場合は、リアルタイムまたは一つ前でやらなければならないが、今回はモノラルで事前計算バッファも使用しないので考慮しない。
また、同じ振幅でも高音域ほど音のエネルギーが大きくなるので、この変換時に音量のキースケーリングもあわせて行った。
◆使用モードの確認
前回の記事で仮定したモードを使用するため、簡易的なリストを用意する。前のプログラム自体は変形分も含んでいるが、今回は紹介があった部分のみだ。
mode = [[[0, 7, 12, 19, 22, 24, 27, 29, 31, 34],
[3, 10, 15, 19, 22, 24, 27, 29, 31, 34]],
[[0, 7, 12, 19, 22, 24, 28, 29, 31, 34],
[4, 10, 16, 19, 22, 24, 28, 29, 31, 34]],
[[0, 7, 12, 19, 23, 24, 28, 29, 31, 35],
[4, 11, 16, 19, 23, 24, 28, 29, 31, 35]],
[[0, 7, 12, 19, 23, 24, 28, 30, 31, 35],
[4, 11, 16, 19, 23, 24, 28, 30, 31, 35]],
[[0, 6, 12, 18, 22, 24, 27, 29, 30, 34],
[3, 10, 15, 18, 22, 24, 27, 29, 30, 34]]]
ud = 0
md = 0
print('first mode: ', md, ' - ', ud)
配列自体は5✕2の構造となっている。前者の5の構造はこの記事の書き方で、はじめからⅥ=Ⅰ、Ⅴ=Ⅶ、Ⅰ=Ⅲ、Ⅳ=Ⅵ、Ⅶ=Ⅱとなっている。後者の2は、主音が=から見て左か右か、という程度のものである。
七音の中からペンタトニックの配列で、ぐるぐる回すというのが前回の趣旨であったが、それを再度確認する。

1小節目から順に、1:Ⅵ=Ⅰ、2:Ⅶ=Ⅱ、3:Ⅰ=Ⅲ、4:Ⅱ=Ⅳ、5:Ⅲ=Ⅴ、6:Ⅳ=Ⅵ、7:Ⅴ=Ⅶ、という名付けにしている(前回記事を参照)。
1、4、5小節目は、本質的でない構造が等しいので一つにまとめている。ただ、実際には機能が違う。
この場合には、いわゆる、ハーモニック・マイナー、メロデック・マイナー、ハーモニック・メジャー等の変化球的スケールは含まれない。が、今回はほぼテストなのでこれで良いだろう。まあ、あまり極端なものはだいたい不気味な響きがするものが多い。ホールトーン・スケールや、コンビネーション・オブ・ディミニッシュにロマンやエクスタシーを感じるなら、もう変態か人外に近いと言って良いだろう。
◆変更強度やリズムの設定
ミュージック・ループ部分のプログラムは、以下のとおりである。初めの 96 という繰り返し部分は、繰り返す単位数で小節かビートみたいなものだ。44000Hz のなかの 43200 のデータが一単位なので、全体としては 90 秒よりすこし少ないくらいチャイムが流れる。
なお、43200 という数字にしたのは、割り算をする時にいろいろ都合がよいからだ。60 という数字で三回も割り切れる。まあ、こういうものは本来なら後で無理やり整数化した方が良いだろう。
初期状態は基本のペンタだが、ときどき変化するようにした。本当は、Ⅶ=Ⅱ ⇔ Ⅳ=Ⅵ を行き帰りするときは、全体(ルートキー)をずらすべきなんだろうが、ややこしくなるので今回はやってない。雰囲気だけは確認できるので、次回までの課題とする。
指定のペンタのなかから、今回は7音分ランダムに配置する。同音は含まれている可能性はあるが、主音が強調される構造にしてあるのでしいて問題はない。
また、リズムは内部で6分割したものを、ランダムではありながら確率分布となるようにした。イメージとしては、
◎◯⦿◎⦿◯
みたいに、2分割でありながら3分割も感じるような確率にした。ただ、リズム位置によって強さが変化するところは、今回はできていない。
for i in range(96):
# mix audio together
audio = np.zeros(43200)
n = 43200
penta = mode[md][ud]
r = random.randint(1, 24)
if r==1 or r==2 or r==3:
ud = (ud + 1) % 2
print('up<->down: ', ud)
elif r==4:
md = (md + 1) % 5
print('mode: ', md)
elif r==5:
md = (md + 4) % 5
print('mode: ', md)
rnd_tone = random.sample(penta, 7)
for i in rnd_tone:
offset = 7200 * random.choice([0, 0, 0, 0, 0, 1, 2, 2, 3, 3, 3, 4, 4, 5])
audio[0 + offset: n] += fm_wave[i][0: n - offset]
# normalize to 16-bit range
audio *= 32767 / (np.max(np.abs(audio)) + 1)
# convert to 16-bit data
audio = audio.astype(np.int16)
# start playback
play_obj = sa.play_buffer(audio, 1, 2, rate)
# wait for playback to finish before exiting
play_obj.wait_done()
◆ミックス時の注意点
ランダムに並べた音を純粋に加算するのだが、その後の処理は注意しなくてはならない。通常、サイン波を考える場合、特に FM 音源ならなおさら、処理時には振幅は ±1にするが、出力時には必要なビット数で整数化(今回は ±32767 に)しなければならない。また、ヘッドルーム効果を今回は作成してないので、単位あたりの出力全体に、最大値または最小値がビット値の上限または下限となるよう、圧縮伸長しノーマライズをかける。
加えて今回は、再生が終わるまで次の計算を待たせてある。計算資源は十分あるものの、これもバッファを再生するようにし、再生が終わらなくならなくても、次の計算を始めていたほうが、小節感の変な間合いは軽減されると思う。これも、次回までの課題だ。
◆その他
ja-ja--n!! とはいわゆるツッチーのことである。どどーん!ともいうから、やはり土でよいのだろう。適当に鳴らして終わりも良いが、いちおう「終わりました」的感じがほしいので追加した。
# ja-ja--n!!
audio = np.zeros((43200, 2))
n = 43200
rnd_tone = penta
for i in rnd_tone:
audio[0: n, 0] += fm_wave[i][0: n]
audio[0: n, 1] += fm_wave[i][0: n]
audio *= 32767 / (np.max(np.abs(audio)) + 1)
audio = audio.astype(np.int16)
play_obj = sa.play_buffer(audio, 2, 2, rate)
# plot-show
plt.plot(sine_wave[:int(rate/hz)+1])
plt.plot(disp_wave[:int(rate/hz)+1])
plt.show()
# wait
play_obj.wait_done()
終わりと同時にプロットショーが現れる。
ここでサイン音と変調された音を比べることができる。
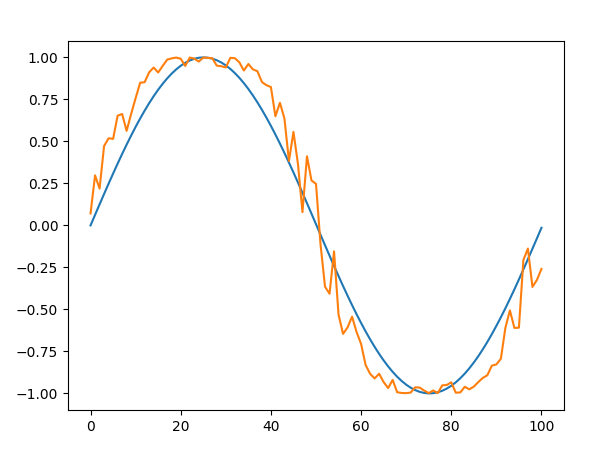
波形上は大した見た目でなくても、聴覚上は大きく異なることがある。ファイナルフラッシュ…FFT はどのみち必要だろう。
もう少し音楽や音だけを簡単に録音し、流せる方法があれば、こんなものができたんですよと説得性をもってもらえるかもしれないが、現状ベストな方法がないのが残念だ。わりと変わった BGM のように、面白い感じにはなっているのだが。
◆今後の予定
改善することも、可能性も、山のようにある。乱数を多く登場させれば、AIみたいなものの導入も考えることができる。構造化には、色彩調和理論のような秩序と変化を概念にいれたものが役立つだろう。まあなんとか続けてみることにする。オリエンタルの風に吹かれてあてもなく、なんてね。
投稿者の人気記事




無料案内所という職業

17万円のPCでTwitterやってるのはもったいないのでETHマイニングを始めた話

京都のきーひん、神戸のこーへん

警察官が一人で戦ったらどのくらいの強さなの?『柔道編』 【元警察官が本音で回答】

機械学習を体験してみよう!(難易度低)

Bitcoinの価値の源泉は、PoWによる電気代ではなくて"競争原理"だった。

テレビ番組で登録商標が「言えない」のか考察してみる

SASUKEオーディションに出た時の話

ジョークコインとして出発したDogecoin(ドージコイン)の誕生から現在まで。注目される非証券性🐶

Bitcoin史 〜0.00076ドルから6万ドルへの歩み〜

海外企業と契約するフリーランス広報になった経緯をセルフインタビューで明かす!
