🙎グラフ理論のすすめ２📏

「愛別離苦、怨憎会苦」なんて言葉がありますが、これは、この世の理不尽さや無常感、あるいは避けられない自己の煩悩を表したりしています。しかし一方で、この世界には「万有引力の法則」という、どんなに好きな相手とも、どんなに嫌いな相手とも、どんなに離れていても、物理学上では同じように「繋がって」しまう、という嬉しくとも残念ともいえる法則があります。その心はいかなるものか、それは分かりませんが…まあ、どんまい💝

さて、変態的なネットワークの前置き話は置きまして、前回の記事に引き続いてグラフ理論の続きです。今回は、グラフ理論を学習する際に簡易に利用できそうな、Python外部ライブラリのNetworkXを取り上げてみます。図画表示する場合はMatplotlibなども必要になります。

【前回記事】

🙋 NetworkXをやってみたよ 🍡

🚅　イントロだくしょん　🚅

NetworkXでは、グラフ理論の概念をほぼほぼそのまま利用できる、というメリットがあります。最近よく感じることなのですが、日本語のある概念のものを「英語」で扱ったとき何と言うのだろう？、ということが割と重要だったりしますが、英語名称も分かるので、そうしたメリットもあります。

参考：日本語ドキュメント

参考：オリジナルドキュメント

まずはインストールです。

(env) $ pip install networkx

matplotlibは無くても、いちおう使うことはできるようです。グラフ理論自体が、必ずしも図画表示を前提条件にしたものではなく、集合や行列等でも表現できるので、それにあったものかなと思います。が、今回はこれを使用してやってみます。

そして、matplotlibを使用する場合は、最初の行に、

from matplotlib import pyplot

表示する時（おそらく最終行になる）に、

networkx.draw(Graff)
pyplot.show()

と追加します。見せかけはpyplotに何もつっこんでませんが、networkx.drawで巻いてるようです。

また、jupyter経由の場合は、最初の行に

%matplotlib inline

を追加するだけです。pyplot.show()は、要りません。

🚅　一つ目を作成　🚅

グラフ全体のオブジェクトの新規作成は、新規グラフをGとすると、単純無向グラフはGraphとなっていますので、

G=networkx.Graph()

ノード(節)をいくつか追加する場合は、一意(ハッシュ可能)な数値や文字列を要素とするリストをListとすると、

G.add_nodes_from(List)

エッジ(辺)をいくつか追加する場合は、両端のノードをそれぞれfrom_node、to_nodeとすると、

G.add_edges_from([*(from_node, to_node)])

でいけます。今回は向きは関係ないので、フロムツーは意味がありませんが…中はノードの場合と同様にリストです。

最後にレンダリングします。

networkx.draw(G)

簡単なものをまとめてみます。

import matplotlib.pyplot as plt
import networkx as nx

# create
G=nx.Graph()

# add nodes
nodes=[1,2,3,4,5]
G.add_nodes_from(nodes)

# add edges
edges=[(1,3),(3,5),(5,2),(2,4),(4,1)]
G.add_edges_from(edges)

# draw and show
nx.draw(G, node_color='y', edge_color='b')
plt.show()

こんなのが出ました🎊

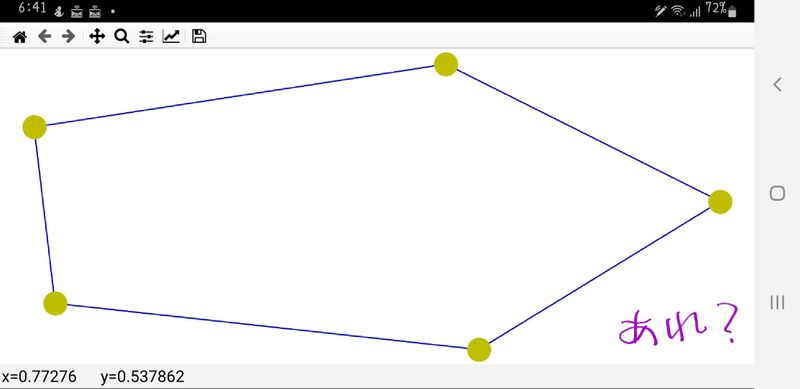
一筆書きの五芒星とただの五角形は、無向グラフでは同じものということが分かります⭐️

💗　変なことをやっちゃうよ　💗

加えたノードが、どのようなものかを確認してみます。

print(G.nodes)
print(type(G.nodes[1]))

print(G.edges)
print(type(G.edges[(1,2)]))

それぞれのノードやエッジの型は、辞書型：dictクラスであることが返ってきます。

辞書型ということは、キーとオブジェクトの組を入れられるので、属性としてバリューや関数、クラスも入れてみます。

以下は、大好きなspamコードです🍜

＃は参考です。

import matplotlib.pyplot as plt
import networkx as nx


# -*- create Graph -*-
# types: Graph, DiGraph, MultiGraph, MultiDiGraph,,,
G=nx.Graph()


# -*- add nodes -*-
nodes=[1,2,3,4,5]
G.add_nodes_from(nodes)
print(G.nodes)
print(type(G.nodes[1]))

G.nodes[1]["weight"]=3
print(G.nodes[1])
# else: => G.add_node(node, **kwargs)
# if attributes are same:
# => G.add_nodes_from(nodes_list, **kwargs)

def nodes_egg(word="Egg"):
	print("This is %s!" % word)
G.nodes[2]["func"]=nodes_egg
G.nodes[2]["func"]("Boiled_Egg")

class Ham:
	def __init__(self, ham="Ham"):
		self.ham=ham
	def spam(self):
		print("I am %s!" % self.ham)

G.nodes[3]["object"]=Ham(ham="Golden_Ham")
G.nodes[3]["object"].spam()


# -*- add edges -*-
edges=[(1,2),(1,3),(2,4),(2,5)]
G.add_edges_from(edges)
print(G.edges)
print(type(G.edges[(1,2)]))

G.edges[(1,2)]["capacity"]=2
print(G.edges[(1,2)])
# else: => G.add_edge(from_node, to_node, **kwargs)
# likewize: => G.add_edges_from(edges_list, **kwargs)

def edge_egg(t=2):
	print("Spam!"*t)
G.edges[(1,3)]["func"]=edge_egg
G.edges[(1,3)]["func"](3)

G.edges[(2,4)]["object"]=Ham(ham="Silber_Spam")
G.edges[(2,4)]["object"].spam()


# draw graph
nx.draw(G)

# show on pyplot
plt.show()

今回、出てきた図画にはあまり意味がありませんので、標準出力を確認してみます。

[1, 2, 3, 4, 5]
<class 'dict'>
{'weight': 3}
This is Boiled_Egg!
I am Golden_Ham!
[(1, 2), (1, 3), (2, 4), (2, 5)]
<class 'dict'>
{'capacity': 2}
Spam!Spam!Spam!
I am Silber_Spam!

自分自身がなにもので、どのようなつながりを持っているかを知ることができないので、改良が必要ですが、とりあえずノードやエッジに機能をもたせることができました☕️

🚅　おまけ　🚅

トップ画面はTermuxですが、ここに行くまでが少し遠いので、試したのはPydroid3です。

アンドロイド派はこれで結構遊べます。

萌え萌えできないのが少々残念ですが…😅

🐤　～おしまい～　🐤