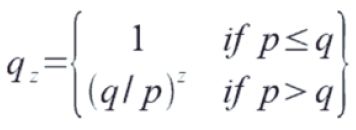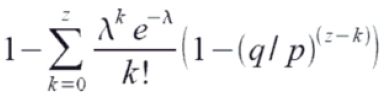ナカモトサトシ論文内Cソース

　ALISでは、ナカモトサトシ論文を読んだことのある人は多いと思います。論文に載っているプログラムを動かしたことはありますか？

プログラムの説明（論文より抜粋）

　攻撃者が正当なチェーンよりも速いスピードで偽のチェーンを作成しようとするシナリオを考えてみる。仮にそれに成功したとしても、コインを無から創り出したり攻撃者自身が所有したことのないコインを盗んだりというようにシステムを自由に操れるようになるわけではない。

　攻撃者が良心的なチェーンに追いつく確率は以下のように計算することができる。

p = 良心的なノードが次のブロックを見つける確率

q = 攻撃者が次のブロックを見つける確率

qz= 攻撃者がzブロックの遅れから追いつく確率

　攻撃者が追いつくことのできる確率を求めるには、彼の行うことのできた仕事量あたりのポアソン分布密度を、その時点での追いつくことができた確率で掛ける。分布の無限テールの加算を避けるために整理すると、以下となる。

式2をCで書いたものが、以下のソースになります。

Cソース

　AttackerSuccessProbability関数はナカモトサトシが書いたものです。main関数は筆者が書き加えました。

#include <stdio.h>
#include <math.h>
double AttackerSuccessProbability(double q, int z)
{
    double p = 1.0 - q;
    double lambda = z * (q / p);
    double sum = 1.0;
    int i, k;
    for (k = 0; k <= z; k++)
    {
        double poisson = exp(-lambda);
        for (i = 1; i <= k; i++)
            poisson *= lambda / i;
        sum -= poisson * (1 - pow(q / p, z - k));
    }
    return sum;
}
int main()
{
    int z;
    double sum, q = 0.1;
    for (z = 0; z <= 10; z++) {
        sum = AttackerSuccessProbability(q, z);
        printf("z=%4d P=%lf\r\n", z, sum);
    }
}

実行結果

論文の11章「計算」に書かれている結果と同じです。

Windows10、Visual Studio 2017でコンパイル・実行しました。

以上