オプションとUniswapでボラを狙い撃つ

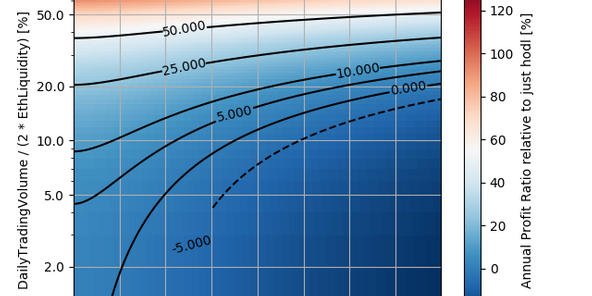
最近の自分の記事で、UniswapのImpermanent lossをput/callオプションの買い(ロングストラドル)でヘッジする考察を行ってきました。

参考:

- オプションでヘッジするUniswap

- [試算編] オプションでヘッジするUniswap

得られた結論は、

r倍の価格変動に起因するUniswapのImpermanent lossを相殺するにはプールポジションのサイズに対して割合aのオプションを買う必要がある:

a = (2 * sqrt(r) - r - 1) / (1 - r)

でした。例えば2倍の価格変動に対するヘッジで必要なオプションサイズは0.17です。このときのImpermanent lossとオプション利益とそれらの和が価格変動に対してどのように変わるかを図にすると以下のようになります。

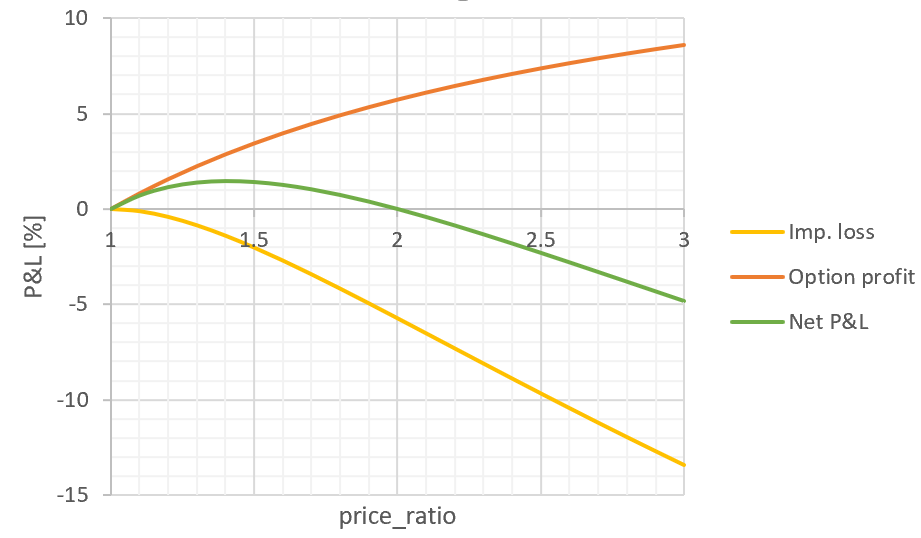
設計通り、Net P&Lはprice_ratio = 2のところでちょうど0になっているのを確認して喜んだのが前回までの記事です。しかし、今回着目したいのはprice_ratio = 1.4付近に最大点があることです。つまり、ちょうどこれくらい価格変動するだろう、という予想のもとに戦略を立てられます。さて、これを一般化してみましょう。

上の図は以下の3つでできています。

・Impermanent loss: 2 * sqrt(r) / (1 + r) - 1

・Option profit: a * (r - 1) / (1 + r)

・Net P&L: (Impermanent loss) + (Option profit)

ここでrはprice ratio、aはオプションサイズです。

Net P&Lの最大点は、この一階微分が0になるところですね。少し複雑ですが、一階微分の分子は次のようになります。

2 * a * sqrt(r) - r + 1 

これが0になるとき、aをrで表せば

a = (r - 1) / (2 * sqrt(r))

となります。つまり、価格がちょうどr倍になるか1/r倍になると見込んでいるなら、Uniswapのプールオプションに対してこのようなaのサイズのオプションを買う、という戦略ができます。

このaをもとのNet P&Lに代入してやれば、変動率rを狙うときの最大リターンを計算できます。式はただ長いので省きますが、図は以下のようになりました。

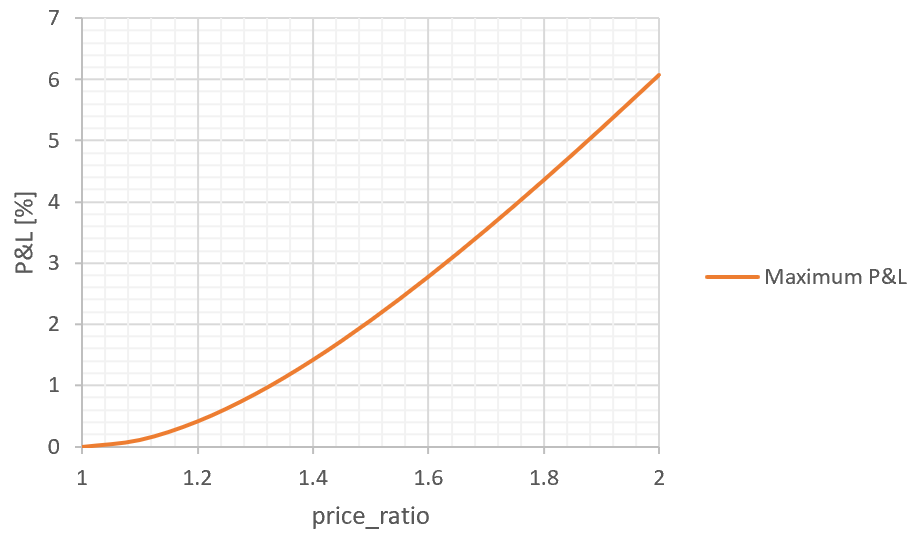
ということで、使う機会があるかはわかりませんが、Uniswapとオプションで特定の価格変動を狙い撃つ戦略のお話でした。