限界貯蓄性向に限界消費性向、限界投資性向……もう限界

前回に見つけた以下の記事について。

「公益財団法人 日本証券経済研究所様の限界消費性向の実証分析」

そもそも「限界消費性向」って何だっけ？！

と、なりました。

限界消費性向とは……以下、引用させて頂きます（コトバンク様より）。

総所得のうち消費にまわる部分の割合を平均消費性向というが，限界消費性向は新たに増加した1単位の所得のうち消費にまわる部分の割合をさす。

つまり「新たに所得が増加した時に、その増加分がどれだけ消費にまわったのかという割合」ということになります。

となりますと、消費にまわらず貯蓄にまわった分は、全体から消費にまわった分を引くと計算できます。

つまり、以下の公式が出てきました。

　〇限界貯蓄性向（S）＝１－限界消費性向（C）

そして、全額を消費ではなく投資をするという場合、上記の「限界消費性向」が、そのまま「限界投資性向」になる……のでしょうか？

コトバンク様で調べると、以下の説明が出てきました（引用致します）。

国民所得の増加が投資支出の増加をもたらす場合における投資の増加分を国民所得の増加分で除した比率。投資支出と国民所得の関係を示すものである。限界投資性向と限界消費性向を加えたものは普通は1より小さいと考えられるが，もしこれが1をこえると経済体系は不安定になる可能性のあることが知られている

……何ですか、これは？？？

さらに調べていくと、熊本学園大学様のこの記事が出てきました。

その記事に「消費関数」に「貯蓄関数」、「投資関数」が出てきました。

上記リンク先様より、グラフを引用させて頂きます。

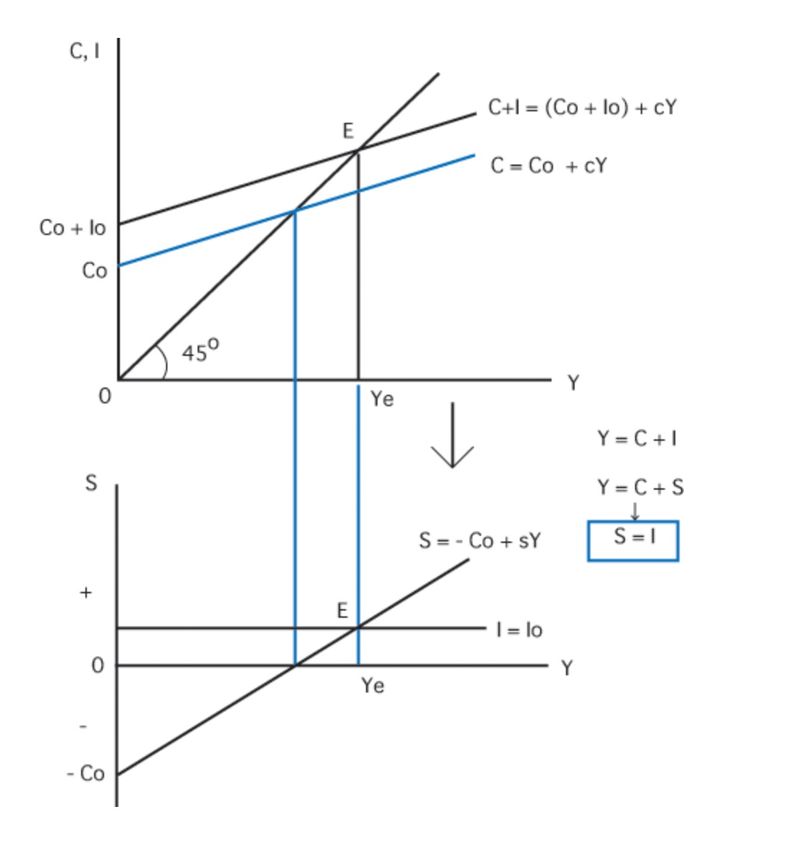
……えーっと……わ、わかんない……。

さらに調べていくと、AI様が以下のようなお言葉を……。

「消費性向と限界消費性向は経済学の用語で、消費性向の微分は限界消費性向です」

微分っ？！

「微分・積分」は、文系だったので学んでいません。

やっぱ、経済をきちんと学ぼうと思ったら、数学はいるな……。

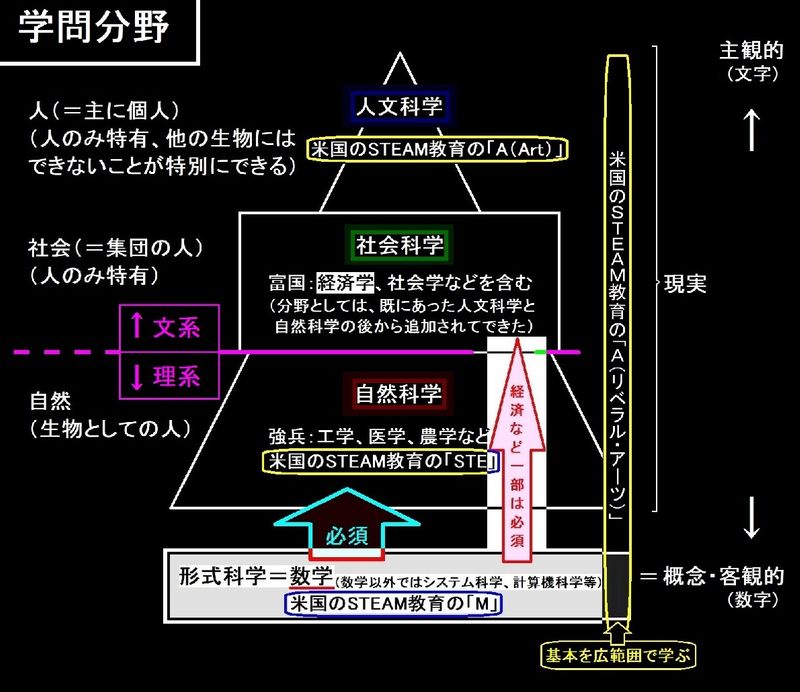
やっぱ、ちゃんと数学を学ばなければなー。

学びなおしどころか、その先を目指さなければなー。

数学は高校の時の、数Ⅰと代数幾何と基礎解析まで。

しかし代数幾何と基礎解析では赤点を取りまくって、二次数学なんて絶対に選択するかー！！！（＝経済学部や経営学部は受験しません）になったはず……

けど、もうちょっときちんと経済を勉強したいなーという気もあるわけで。

調べてみると、以下の本が出てきました。

……ホンマにめっちゃやさしいんか？？？

微分積分、いい気分～♪

……なわけないっちゅーねん。